Operational reliability evaluation of restructured power systems with wind power penetration utilizing reliability network equivalent and time-sequential simulation approaches

Abstract

In the last two decades, the wind power generation has been rapidly and widely developed in many regions and countries for tackling the problems of environmental pollution and sustainability of energy supply. However, the high share of intermittent and fluctuating wind power production has also increased the burden of system operator for securing power system reliability during the operational phase. Moreover, the power system restructuring and deregulation have not only introduced the competition for reducing cost but also changed the strategy of reliability evaluation and management of power systems. The conventional long-term reliability evaluation techniques have been well developed, which have been more focused on planning and expansion rather than operation of power systems. This paper proposes a new technique for evaluating operational reliabilities of restructured power systems with high wind power penetration. The proposed technique is based on the combination of the reliability network equivalent and time-sequential simulation approaches. The operational reliability network equivalents are developed to represent reliability models of wind farms, conventional generation and reserve provides, fast reserve providers and transmission network in restructured power systems. A contingency management schema for real time operation considering its coupling with the day-ahead market is proposed. The time-sequential Monte Carlo simulation is used to model the chronological characteristics of corresponding reliability network equivalents. A simplified method is also developed in the simulation procedures for improving the computational efficiency. The proposed technique can be used to evaluate customers’ reliabilities considering high penetration of wind power during the power system operation in the deregulated environment.

1 Introduction

In recent years, the development and utilization of wind power generation have been rapidly expanding in many regions and countries for reducing reliance on conventional energy resources and reducing environmental pollutants. Wind power generation is a promising renewable energy resource, which can compete with conventional power generation in terms of abundance, accessibility and production cost. Wind energy will play an important role in the European Union’s (EU) future energy plan [1]: For example, wind power will provide 50% of electricity production by 2025 [2] in Denmark. However, the fluctuation of wind velocity varying chronologically and random nature of failures of WTGs make the generation output of wind farm stochastic and totally different from that of the conventional generating units [3]. The high penetration of intermittent and fluctuating wind power production can therefore bring complexities for securing proper balancing between generation and demand and maintaining system reliabilities during the operational phase. The fluctuating wind power production can result in system imbalances [4]: In Denmark, more than half of the system imbalances are caused by wind power fluctuation, which will be more frequent with the increasing penetration of wind power production in the future.

There are two categories of reliability evaluation methods for power systems with wind power generation including analytical techniques [3, 5, 6] and Monte Carlo simulation approaches [7, 8]. Direct mathematical methods such as universal generating functions [9, 10] are utilized by analytical techniques for evaluating system and customers’ reliability indices for determined states. Monte Carlo simulation approaches is more flexible for considering the chronological characteristics of power system operation [7], hence they can provide more detailed and accurate information on the reliability indices of power system operation. Moreover Monte Carlo simulation approaches are more suitable when considering complex operational conditions or when the number of contingency events is large [11].

These research works mainly focus on the long term reliability evaluation based on the steady-state probabilities of system components. They are mainly utilized for planning and expansion of power systems considering high wind power penetration [9].

However, these methods can only provide a rough approximation of reliability indices in the operational phase because of high fluctuations of wind power generation. Moreover these developed methods are more concerned on the conventional integrated power systems. The restructuring of power system changes the basic reliability management strategies of system operation and planning [12]. Electric energy and reserve are traded in various electricity markets in restructured power systems. These markets are correlated with the real time operation of power systems, which may have significant impacts on system and customers’ reliabilities in the operational stage. These changes make contingency management schema more complicated than that used in conventional integrated power systems.

This paper proposes a technique for evaluating operational reliabilities of restructured power systems with high wind power penetration. The proposed technique is based on the combination of the reliability network equivalent and time-sequential simulation approaches. The reliability network equivalents are developed to represent operational reliability models of conventional generation and reserve providers, wind farms, fast reserve providers and transmission network in restructured power systems. The time-sequential Monte Carlo simulation is used to model the chronological characteristics of corresponding reliability network equivalents. A contingency management schema for real time operation considering its coupling with the day-ahead market is proposed. A simplified method is developed in the simulation procedures for improving the computational efficiency. The proposed technique can be used to evaluate customers’ reliabilities considering high penetration of wind power during the power system operation in the deregulated environment.

2 Reliability network equivalents of generation systems

2.1 Operational reliability equivalents of wind farms

Electric power generation from a wind farm is strongly dependent on the intermittent and fluctuating wind speed, which has great uncertainty due to the random nature of the weather. A well-known model used in the reliability evaluation of power systems with wind power generation is the Markov process model [3, 9, 13].

In the operational phase, the Markov process model can also be used to predict probabilities of future wind states, whose future development depends only on the present state and not on how the process arrived at that state [14]. The wind speed model is modelled as a continuous-time Markov chain illustrated in Fig. 1. As shown in Fig. 1, the wind speed V^w(t) at any time t is a random variable taking values from the wind speed set $\{ v_{1} , \ldots ,v_{{K^{w} }} \} .$

Fig. 1

State space diagram for wind speed model

The Markov chain model assumes that the state transition depends on its present state [11, 14]. In the operational phase, the probabilities of future wind states are also strongly dependent on transition rates among the present wind state and possible future wind states. For a given operation period, e.g., in the evening, the current wind speed is in the state j^w and $\sum\limits_{s = 1}^{{K^{w} - j^{w} }} {\lambda_{{j^{w} ,j^{w} + s}} } > \sum\limits_{s = 1}^{{j^{w} - 1}} {\lambda_{{j^{w} ,j^{w} - s}} }$, it is more probable that wind speed will increase. Similarly if $\sum\limits_{s = 1}^{{K^{w} - j^{w} }} {\lambda_{{j^{w} ,j^{w} + s}} } < \sum\limits_{s = 1}^{{j^{w} - 1}} {\lambda_{{j^{w} ,j^{w} - s}} }$, e.g., in the day, it shows that the probability of wind speed decrease is higher than the wind speed increase.

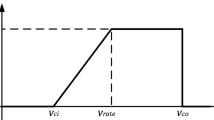
The following equation (1) is used to evaluate the power output wp _l (t) of WTG l at time t corresponding to wind speed V^w(t) [16]:

$$ wp_{l} (t) = \left\{ {\begin{array}{*{20}c} 0 & {0 \le V^{w} (t) \le V_{ci,l}^{w} } \\ {\left( {A_{l} + B_{l} \times V^{w} (t) + C_{l} \times V^{w} (t)_{{}}^{2} } \right) \cdot P_{r,l} } & {V_{ci,l}^{w} \le V^{w} (t) \le V_{r,l}^{w} } \\ {P_{r,l} } & {V_{r,l}^{w} \le V^{w} (t) \le V_{co,l}^{w} } \\ 0 & {V^{w} (t) \ge V_{co,l}^{w} } \\ \end{array} } \right. $$

(1)

where A _l , B _l and C _l are operational parameters of the WTG l presented in [16], respectively. The cut-in speed, the cut-out speed, the rated speed and the rated power of the WTG l are V ^w_ci,l , V ^w_co,l , V ^w_r,l and P_r,l, respectively. The power output at time twp _l (t) take values from the set $\{ wp_{l,1}^{{}} , \cdots ,wp_{{l,j^{w} }}^{{}} , \cdots ,wp_{{l,K^{w} }}^{{}} \} .$ The power output of WTG l corresponding to wind state $v_{{j^{w} }}$ is $wp_{{l,j^{w} }}^{{}}$.

A wind farm usually consists of many WTGs and trades its generation in the day-ahead market, which usually has an hourly time resolution, e.g. the Nordic electricity market [17]. However, the hourly time resolution in the day-ahead market is a rough approximation of the generation of wind farms, which cannot handle the generation fluctuations and possible failures of WTGs during the operational hour. In real time operation, the power output of a wind farm is determined by the power output of each WTG for time t, which can be obtained as:

$$ WP_{i} (t) = \sum\limits_{l = 1}^{{n_{i}^{w} }} {wp_{li} (t)} $$

(2)

where n ^w _i is the number of WTGs in the wind farm at bus i.

Suppose the scheduled generated power of the wind farm at bus i for the operational hour h in the day-ahead market is WP ^h,D _i . The difference between $WP_{i} (t )$ and WP ^h,D _i is the imbalance of the wind farm at time t because of wind power fluctuation, where h ≤ t < h + 1:

$$ \Delta \,WP_{i} (t) = WP_{i} (t) - WP_{i}^{h,D} $$

(3)

If ΔWP _i (t) < 0, it indicates that the power output of the wind farm at time t is less than the scheduled value in the day-ahead market, which needs to be compensated by up regulation. Similarly if ΔWP _i (t) > 0, it indicates that the wind farm at time t can generate more power than the scheduled value in the day-ahead market, which can either be sold in the real-time market or spilled.

If only the stochastic behavior of wind speed is considered, WP _i (t) is a random variable taking value from the set $\{ WP_{i,1}^{{}} , \cdots ,WP_{{i,j_{i}^{w} }}^{{}} , \cdots ,WP_{{i,K_{i}^{w} }}^{{}} \} = \{ {\sum\limits_{l = 1}^{{n_{i}^{w} }} {wp_{l,1}^{{}} } , \cdots ,\sum\limits_{l = 1}^{{n_{i}^{w} }} {wp_{{l,j^{w} }}^{{}} } , \cdots ,\sum\limits_{l = 1}^{{n_{i}^{w} }} {wp_{{l,K^{w} }}^{{}} } } \}$. The random failures of WTGs can also derate the power output of a wind farm. In this case, WP _i (t) is the random variable taking the value from the set $\{ {\sum\limits_{l = 1}^{{n_{i}^{w} }} {wp_{l,1}^{{}} } ,\sum\limits_{l = 1}^{{n_{i}^{w} - 1}} {wp_{l,1}^{{}} } , \ldots ,\sum\limits_{l = 1}^{{n_{i}^{w} }} {wp_{{l,j^{w} }}^{{}} } ,\sum\limits_{l = 1}^{{n_{i}^{w} - 1}} {wp_{{l,j^{w} }}^{{}} } , \ldots ,\sum\limits_{l = 1}^{{n_{i}^{w} }} {wp_{{l,K^{w} }}^{{}} } ,\sum\limits_{l = 1}^{{n_{i}^{w} - 1}} {wp_{{l,K^{w} }}^{{}} } , \ldots ,0} \}$ considering both the stochastic behavior of wind speed and random failures of WTGs. For a specific state of wind farm $J^{\hat{w}}$, the power output of the wind farm at bus i is

$$ W{P_{{i,j^{{\hat{w}} }}} = \sum\limits_{l = 1}^{{n_{i}^{w} - {n_{{j^{\hat{w}}} }}^{f} }} }{wp_{{l,j^{w} }} } $$

(4)

Equation (4) indicates that wind speed V^w(t) is in state $j_{{_{{}} }}^{w}$ and there are $n_{{ j^{\hat{w}} }}^{f}$ WTGs failed. The Markov model for representing the stochastic power output of the wind farm is represented in Fig. 2. The state transitions between non-adjacent states are not illustrated in Fig. 2 for the sake of clarity [13].

Fig. 2

Markov model the wind farm considering stochastic wind speed and random failures of WTGs

Reliability network equivalent techniques have been successfully used to represent reliability models of market participants in the restructured power systems [18–21]. The operational reliability model of a wind farm at bus i can be represented as an equivalent operational multi-state wind generation provider (EOWP). The characteristics of an EOWP depend on the power generation of the wind farm and its coupling with the day-ahead market such as the imbalance of the wind farm with the scheduled wind generation in the operational phase.

The following time-sequential simulation procedures are used to determine the characteristics of an EOWP.

Step 1: Suppose the initial state of the EOWP in operational phase is ${{j^{\hat{w}} }}$. Determine the corresponding power output $WP_{{i,j_{{}}^{\hat{w}} }}^{{}}$ based on (4).

Step 2: Generate a random number and convert the number to the time period of the state $D_{{j^{\hat{w}} }}$ following the corresponding exponential distribution

$$ \left[ {\sum\limits_{\begin{subarray}{l} s^{w} = 1 \\ s^{w} \ne j^{w} \end{subarray} }^{{K^{w} }} {\lambda_{{j^{w} ,s^{w} }} } + \left( {n_{i}^{w} - n_{{j^{\hat{w}} }}^{f}}\right)\lambda_{i}^{w} + \mu_{i}^{w} } \right] \cdot e^{^{{ - \left[ {\sum\limits_{\begin{subarray}{l} s^{w} = 1 \\ s^{w} \ne j^{w} \end{subarray} }^{{K^{w} }} {\lambda_{{j^{w} ,s^{w} }} } + \left( {n_{i}^{w} - n_{{j^{\hat{w}} }}^{f} } \right)\lambda_{i}^{w} + \mu_{i}^{w} } \right]t}}}. $$

If the number of failed WTGs is zero in the state, the exponential distribution has become $\left[ {\sum\limits_{\begin{subarray}{l} s^{w} = 1 \\ s^{w} \ne j^{w} \end{subarray} }^{{K^{w} }} {\lambda_{{j^{w} ,s^{w} }} } + n_{i}^{w} \lambda_{i}^{w} } \right] \cdot e^{^{{ - \left[ {\sum\limits_{\begin{subarray}{l} s^{w} = 1 \\ s^{w} \ne j^{w} \end{subarray} }^{{K^{w} }} {\lambda_{{j^{w} ,s^{w} }} } + n_{i}^{w} \lambda_{i}^{w} } \right]t}}}$. The imbalance of the wind farm at time t can be evaluated as:

$$ \Delta \,WP_{{i,j_{{}}^{\hat{w}} }}^{{}} (t) = WP_{{i,j_{{}}^{\hat{w}} }}^{{}} - WP_{i}^{h,D} \, $$

(5)

where h ≤ t < h + 1 and $t \le D_{{j^{\hat{w}} }}$.

Step 3: Determine the next state of the wind farm $s^{{\hat{w}}}$ based on the system state transition sampling technique [22].

Step 4: Evaluate the corresponding power output $WP_{{i,s_{{}}^{\hat{w}} }}^{{}}$ and the time period of the state $D_{{s^{\hat{w}} }}$ as step 2. The imbalance of the wind farm for the state $D_{{s_{{}}^{\stackrel{\frown}{w}} }}$ at time t can also be calculated as (5).

Step 5: Repeat step 3 to step 4 till the sampled total duration has reached the studied operational period.

2.2 Operational reliability equivalents of conventional generation and reserve provides

In restructured power systems, a conventional generation and reserve provider usually consists of several large conventional generating units for trading electric energy and reserve in various forward and balancing markets [21]. The large generating units are economically dispatched in the normal operation and can provide balancing power during a contingency state. These generating units still play an important role for providing electricity and maintaining system and customers’ reliabilities in existing power systems.

A conventional generating unit has both the characteristics of controllability and stochastic behavior. A conventional generating unit l with installed capacity IC _l has a scheduled power SP ^h _l for the operational hour h, SP ^h _l  < IC _l , which usually is determined in the day-ahead market. The generating unit l usually also has an operating reserve margin, ΔP ^h _l , e.g. primary reserve, which can be controlled and activated in real time for maintaining system reliability and security in the operational hour h. Let DC ^h _l be the dispatchable generating capacity of the unit, in the operational hour h, where DC ^h _l  = SP ^h _l  + ΔP ^h _l and DC ^h _l  ≤ IC _l . Therefore, if the generating unit l is functioning well, it will be controlled for producing power within the limit of DC _l in the operational hour.

The stochastic behaviors of conventional generating units are caused by random failures. The random failures of generating units can reduce the available generating capacity completely or partially. The reliability model for a conventional generating unit can be represented as a binary-state model or a more complex multi-state model. Multi-state representations of generating units especially for large generators provide a more accurate and flexible tool in generating capacity adequacy assessment. A typical example is a coal fired unit with a nominal generating capacity of 576 MW used in real world [23], which is represented as a four-state reliability model as shown in Fig. 3. Assume that the scheduled power and primary reserve provided by the coal fired unit are 500 MW and 28 MW, respectively. Therefore the dispatchable generating capacity of the coal fired unit is 528 MW in the well functioning state, which indicates the maximum power which can be produced in real time. In the complete failure state, the available generating capacity is zero and therefore the generation output is also zero. In a derated state, e.g. state 3, the available generating capacity is only 482 MW, which indicates that the produced power of the coal fired unit will be reduced to 482 MW.

Fig. 3

The dispatchable generating capacities of the coal fired unit

In general, a conventional generating unit l can have K ^g _l states, K ^g _l  ≥ 2. The evolution of unit l produces the stochastic process of the available generating capacity $GC_{l}^{{}} (t) \in \{ GC_{l,1}^{{}} , \cdots ,GC_{{l,j_{l}^{g} }}^{{}} , \cdots ,GC_{{l,K_{l}^{g} }}^{{}} \}$. The available generating capacity for each state j ^g _l , j ^g _l  = 1, ···, K ^g _l , is $GC_{{l,j_{l}^{g} }}^{{}}$.

The dispatchable generating capacity of the generating unit l for each unit state j ^g _l in the operational hour h can be evaluated as:

$$ DC_{{l,j_{l}^{g} }}^{h} = \hbox{min} \left\{ {\left( {SP_{l}^{h} +\Delta \,P_{l}^{h} } \right),GC_{{l,j_{l}^{g} }}^{{}} } \right\} $$

(6)

The generation and reserve provider at bus i can have $n_{{j^{\hat{w}} }}^{f}$ conventional generating units, which can be represented as a multi-state Markov model. The operational reliability model of a generation and reserve provider at bus i can be represented as an equivalent operational multi-state generation and reserve provider (EOGRP). The available generating capacity of the EOGRP is a random variable at time t taking values from $\{ AG_{i,1} , \cdots ,AG_{{i,j_{{}}^{G} }} , \cdots ,AG_{{i,K_{{}}^{G} }} \} .$ The available generating capacity of the EOGRP for each state j^G can be evaluated as:

$$ AG_{{i,j_{{}}^{G} }} = \sum\limits_{l = 1}^{{n_{i}^{g} }} {DC_{{l,j_{l}^{g} }}^{h} } $$

(7)

The EOGRP can trade its generation and operating reserve in the day-ahead energy and reserve markets, which are supposed as GP^h,D and GR^h,D for the operational hour h, respectively. The characteristics of an EOGRP are determined by the dispatchable generating capacity in real time considering the impact of generation and reserve scheduling in the day-ahead market.

The dispatchable generating capacity of the EOGRP for state j^G at time t can be evaluated as:

$$ DG_{{i,j_{{}}^{G} }} (t) = \hbox{min} \left\{ {AG_{{i,j_{i}^{G} }} ,\left( {GP_{{}}^{h,D} + GR_{{}}^{h,D} } \right)} \right\} $$

(8)

where h ≤ t < h + 1 and $t \le D_{{j^{G} }}$.

If $GP_{{}}^{h,D} \le DG_{{i,j_{{}}^{G} }} (t) < \left( {GP_{{}}^{h,D} + GR_{{}}^{h,D} } \right)$, it indicates that the EOGRP cannot provide sufficient operating reserve and can satisfy the scheduled generation requirement for the operational hour h. If $DG_{{i,j_{{}}^{G} }} (t) < GP_{{}}^{h,D}$, it indicates that the EOGRP is even short of available capacity for satisfying the scheduled generation requirement for the operational hour h.

The following time-sequential simulation procedures are used to determine the characteristics of an EOGRP.

Step 1: Suppose the initial state of the EOGRP in operational phase is j^G. Determine the corresponding available generating capacity $AG_{{i,j_{{}}^{G} }}$ and dispatchable generating capacity $DG_{{i,j_{{}}^{G} }} (t)$ based on (7) and (8), respectively.

Step 2: Generate a random number and convert the number to the time period of the state $D_{{j_{{}}^{G} }}$ following the corresponding exponential distribution. $\left[ {\sum\limits_{\begin{subarray}{l} s^{G} = 1 \\ s^{G} \ne j^{G} \end{subarray} }^{{K^{G} }} {\lambda_{{j^{G} ,s^{G} }} } } \right] \cdot e^{^{{ - \left[ {\sum\limits_{\begin{subarray}{l} s^{G} = 1 \\ s^{G} \ne j^{G} \end{subarray} }^{{K^{G} }} {\lambda_{{j^{G} ,s^{G} }} } } \right]t}}}$.

Step 3: Determine the next state of the EOGRP s^G based on the system state transition sampling technique [22].

Step 4: Evaluate the corresponding available generating capacity $AG_{{i,s_{{}}^{G} }}$ and dispatchable generating capacity $DG_{{i,s_{{}}^{G} }} (t)$, and the time period of the state $D_{{s_{{}}^{G} }}$ as step 2.

Step 5: Repeat step 3 to step 4 till the sampled total duration has reached the studied operational period.

2.3 Operational reliability equivalents of fast reserve providers

Besides the large online generating units, the rapid start-up generating units can start-up and synchronize with the system in a very short lead time. The rapid start-up generating units are usually utilized for providing additional operating reserve in contingency states.

Similar to the conventional online generating unit, the rapid start-up unit also has both the characteristics of controllability and stochastic behavior. Moreover, the frequent start-up can lead to extra starting stress of generating units.

If the unit starts up successfully and transits to the in-service state, the unit has the controllability for providing the necessary reserve. However, if the unit fails to start-up or meets a random failure during operation, it goes into the failure state, where the generation output of the unit is zero and the controllability of the unit is lost. The transitions among different states are also followed by the stochastic behaviors of the unit. The rapid start-up generating unit can be represented as a three-state model [24], which neglects repair in the short operational phase, as illustrated in Fig. 4.

Fig. 4

State space diagram for the rapid start-up unit

Once committed, a unit initially in the ready-for-service state (state 0) can start up successfully to the in-service state (state 2). In the in-service state, the generating unit is controlled for the generation output within the limit of corresponding available capacity. Or the unit can fail to start-up and transit to the failure state (state 1). In the failure state, the generation output of the unit is zero and the controllability of the unit is lost. The transition rate between state 0 and state 2, and the transition rate between state 0 and state 1 are (1 − p _s )/T and p _s /T, where p _s , T and λ_2,1 are the start-up failure probability, the average shut-down time between periods of commitment and failure rates from the in-service state to the failure state, respectively.

The fast reserve provider at bus i can have n ^f _i rapid start-up generating units. The operational reliability model of a fast reserve provider at bus i can be represented as an equivalent operational multi-state fast reserve provider (EFRP). The available reserve capacity of the EFRP is a random variable at time t taking values from $\{ AR_{i,1} , \cdots ,AR_{{i,j_{{}}^{f} }} , \cdots ,AR_{{i,K_{{}}^{f} }} \}$. The available reserve capacity of the EFRP for each state j^f can be evaluated as:

$$ AR_{{i,j_{{}}^{f} }} = \sum\limits_{l = 1}^{{n_{i}^{f} }} {AG_{{l,j_{l}^{f} }}^{{}} } $$

(9)

where $AG_{{l,j_{l}^{f} }}^{{}}$ is the available generating capacity of the unit l for the corresponding state.

The EFRP can schedule operating reserve in the forward reserve market or through bilateral contract, which is supposed as FR^h,D for the operational hour h. The characteristics of an EFRP are determined by the dispatchable reserve capacity in real time.

The dispatchable reserve capacity of the EFRP for state j^f at time t can be evaluated as:

$$ DR_{{i,j_{{}}^{f} }} (t) = \hbox{min} \left\{ {AR_{{i,j_{{}}^{f} }} ,FR_{{}}^{h,D} } \right\} $$

(10)

where h ≤ t < h + 1 and $t \le D_{{j^{f} }}$.

The following time-sequential simulation procedures are used to determine the characteristics of an EFRP.

Step 1: Suppose the initial state of the EFRP in operational phase is j^f. Determine the corresponding available reserve capacity $AR_{{i,j_{{}}^{f} }}$ and dispatchable reserve capacity $DR_{{i,j_{{}}^{f} }} (t)$ based on (9) and (10), respectively.

Step 2: Generate a random number and convert the number to the time period of the state $D_{{j_{{}}^{f} }}$ following the corresponding exponential distribution. $\left[ {\sum\limits_{\begin{subarray}{l} s^{f} = 1 \\ s^{f} \ne j^{f} \end{subarray} }^{{K^{f} }} {\lambda_{{j^{f} ,s^{f} }} } } \right] \cdot e^{^{{ - \left[ {\sum\limits_{\begin{subarray}{l} s^{f} = 1 \\ s^{f} \ne j^{f} \end{subarray} }^{{K^{f} }} {\lambda_{{j^{f} ,s^{f} }} } } \right]t}}}$.

Step 3: Determine the next state of the EFRP s^f based on the system state transition sampling technique [22].

Step 4: Evaluate the corresponding available reserve capacity $AR_{{i,s_{{}}^{f} }}$ and dispatchable reserve capacity $DR_{{i,s_{{}}^{f} }} (t)$, and the time period of the state $D_{{s_{{}}^{f} }}$ as step 2.

Step 5: Repeat step 3 to step 4 till the sampled total duration has reached the studied operational period.

3 Contingency management schema for real time operation

If there is generation inadequacy for a contingency state, generation and reserve has to be re-dispatched and load may be curtailed to maintain the balance of system operation. The transmission network violation can also affect the electricity deliverability from the generation and reserve providers to bulk load points (BLP) [18]. The operational reliability model of the transmission network between the generation and reserve providers and a BLP can be represented as an equivalent operational multi-state transmission provider (EMTP).

For determining the possible load curtailment at each BLP in the contingency state, a contingency management schema is proposed as shown in Fig. 5, which is formulated as an optimal power flow (OPF) model. The day-ahead scheduling of wind power, the wind power fluctuation during real time operation, the dispatchable generating capacity and the dispatchable reserve capacity of the EOGRP and the EFRP considering their coupling with the forward electricity markets, and network constraints are included in the model.

Fig. 5

Contingency management schema for real time operation

The objective of the OPF model is to minimize the total system load curtailment for the contingency state j considering network constraints and market scheduling and coupling during the real time operation.

For contingency state j, the objective function is:

$$ \text{Min} \,\,\,f_{j} = \sum\limits_{i = 1}^{N} {LC_{{j_{i} }} } (t) $$

(11)

where $LC_{{j_{i} }}^{{}} (t)$ is the load curtailment at BLP i for contingency state j at time t.

The objective function is subject to the following constraints for contingency state j:

DC power flow constraints:

$$ \varvec{B}_{j}\varvec{\theta}_{j} (t){ = }\left( {\varvec{WP}^{h,D} { + }\Delta \,\varvec{WP}_{j}^{{}} (t)} \right){ + }\varvec{PG}_{j}^{{}} (t) + \varvec{PR}_{j}^{{}} (t) + \varvec{LC}_{j} (t)\,{ - }\,\bar{\varvec{D}}(t) $$

(12)

where $\varvec{B}_{j}^{{}}$ is the admittance matrix of the network; $\varvec{\theta}_{j} (t)$ is phase angle vector of bus voltages at time t; $\varvec{WP}^{h,D} = [WP_{1}^{h,D} , \cdots ,WP_{N}^{h,D} ]^{\text{T}}$ is the vector of scheduled wind generations for the operational hour h in the day-ahead market; $\Delta \,\varvec{WP}_{j}^{{}} (t) = \left[ {\Delta \,WP_{{1,j^{\stackrel{\frown}{w}} }}^{{}} (t), \cdots ,\Delta \,WP_{{N,j^{\stackrel{\frown}{w}} }}^{{}} (t)} \right]^{\text{T}}$ is the vector of wind generation imbalance at time t caused by wind power fluctuation; $\varvec{PG}_{j}^{{}} (t) = [PG_{{1,j_{{}}^{G} }} (t), \cdots ,PG_{{N,j_{{}}^{G} }} (t)]^{\text{T}}$ is the vector of power generations of EOGRPs at time t; $\varvec{PR}_{j}^{{}} (t) = [PR_{{1,j_{{}}^{f} }} (t), \cdots ,PR_{{N,j_{{}}^{f} }} (t)]^{\text{T}}$ is the vector of reserve dispatched of EFRPs at time t; $\varvec{LC}_{j} (t) = [LC_{1,j} (t), \cdots ,LC_{N,j} (t)]^{\text{T}}$ is the vector of load curtailment at time t; $\bar{\varvec{D}}(t) = [\bar{D}_{1} (t), \cdots ,\bar{D}_{N} (t)]^{\text{T}}$ represents the vector of the forecasted bus loads for the normal state at time t.

Equations (12) represents that the system has to be balanced with the wind power fluctuation from the day-ahead scheduling and system load after the generation re-dispatch of EOGRPs, fast reserve dispatch of EFRPs and load curtailments.

Load curtailment constraints:

$$ 0 \le LC_{i,j} (t) \le LC_{i,j}^{\hbox{max} } $$

(13)

Generation output limits of EOGRPs:

$$ 0 \le PG_{{i,j_{{}}^{G} }} (t) \le DG_{{i,j_{{}}^{G} }} (t) $$

(14)

Fast reserve dispatch limits of EFRPs:

$$ 0 \le PR_{{i,j_{{}}^{f} }} (t) \le DR_{{i,j_{{}}^{f} }} (t) $$

(15)

Line flow constraints:

$$ \left| {\frac{1}{{x_{{j_{ik} }} }}\left( {\theta_{{j_{i} }} (t) - \theta_{{j_{k} }} (t)} \right)} \right| \le \left| {F_{ik}^{\hbox{max} } } \right| $$

(16)

where $\theta_{{j_{i} }} (t)$ is the phase angle of voltage at bus j at time t; $x_{{j_{ik} }}$ and |F ^max _ik | are the reactance and maximum power flow of the line between buses i and k respectively.

4 Simulation procedures and reliability evaluation

The time-sequential Monte Carlo simulation can be extremely costly if the proposed contingency management schema is conducted for analyzing each sampled state by OPF. Therefore it is important to develop a simplified method for improving the computational efficiency of simulation procedures.

In this paper, it is assumed that the system is coherent: if a failed component has been repaired, the system performance would never be worse; conversely, if a working component has failed, the system performance would not be better [26]. The possible system states can be further split into reliable states, marginal successful states and failure states as shown in Fig. 6.

Fig. 6

Power system evolution among state space

• 1) Reliable state: In this state, the generation system has adequate dispatchable capacity and transmission network is intact. The adequate dispatchable capacity indicates that the total dispatchable generating and reserve capacities from the wind farms, EOGRPs and the EFRPs are larger than the system demand plus a reserve margin:

$$ \sum\limits_{{i = 1}}^{N} {\left( {\Delta {\kern 1pt} WP_{{i,j^{{\hat{w}}} }} (t) + WP_{i}^{{h,D}} } \right)} + \sum\limits_{{i = 1}}^{N} {DG_{{i,j^{G} }} (t)} + \sum\limits_{{i = 1}}^{N} {DR_{{i,j^{f} }} (t)} \ge \sum\limits_{{i = 1}}^{N} {\bar{D}_{i} (t)} + RM $$

(17)

where RM is the pre-defined reserve margin.

The adequate dispatchable capacity can guarantee the demand will not be shed because of insufficient generation capacity. The intact transmission network indicates that the system has sufficient transmission capacity for delivering generation to the demand. In this state, the contingency management schema OPF is not necessary to be conducted because the system has sufficient margin for preventing load curtailment. The reliable state can be easily determined if (17) can be satisfied and the transmission network is intact.

• 2) Marginal successful state: As shown in Fig. 6, the system can transit from a reliable state to another state because of the failure of a system component. The failure of a transmission line or a generating unit may lead to possible network violations or inadequate dispatchable capacity, respectively. If two criterions of the reliable state cannot be satisfied, the contingency management schema will be implemented for determining the possible load curtailment at each BLP. In this case, if there is not any load curtailment, the power system is in the marginal successful state indicating that the system is still successful but may not have sufficient margin.

• 3) Failure state: In this state, there exists load curtailment caused by inadequate generation capacity or network violations, which is determined by the contingency management schema. The system can transit from the failure state to a reliable state or a marginal successful state if failed components have been repaired.

The sequential simulation procedure for evaluating reliability indices consists of the following steps.

Step1: Generate the state sequence of the EOWP at each bus for the studied operational period, e.g. 24 hours, utilizing the approach described in Section 2.A. From the sampled sequence, determine the state $j^{\hat{w}}$ of the EOWP at time t.

Step2: Generate the state sequence of the EOGRP at each bus for the studied operational period utilizing the approach described in Section 2.B. From the sampled sequence, determine the state j^Gof the EOGRP at time t.

Step3: Generate the state sequence of the EFRP at each bus for the studied operational period utilizing the approach described in Section 2.C. From the sampled sequence, determine the state j^fof the EFRP at time t.

Step4: Similar procedures as Section 2 are used to generate the state sequence of the EMTP for the studied operational period. From the sampled sequence, determine the state j^L of the EMTP at time t.

Step5: Determine the total wind power output, dispatchable generating capacity and dispatchable reserve capacity of the system for time t, which can be evaluated as:

$$ \sum\limits_{{i = 1}}^{N} {\left( {\Delta {\kern 1pt} WP_{{i,j^{{\hat{w}}} }} (t) + WP_{i}^{{h,D}} } \right)} {\kern 1pt} {\text{and}}{\kern 1pt} \$ \$ \sum\limits_{{i = 1}}^{N} {DG_{{i,j^{G} }} (t)} ,\sum\limits_{{i = 1}}^{N} {DR_{{i,j^{f} }} (t)} , $$

respectively. If

$$ \sum\limits_{i = 1}^{N} {\left( {\Delta \,WP_{{i,j_{{}}^{\hat{w}}}}^{{}} (t) + WP_{i}^{h,D} } \right)} + \sum\limits_{i = 1}^{N} {DG_{{i,j_{{}}^{G} }} (t)} + \sum\limits_{i = 1}^{N} {DR_{{i,j_{{}}^{f} }} (t)} - TD(t) \ge RM $$

where RM is the reserve margin determined by the system operator and TD(t) is the total system demand at time t, and the sampled EMTP state j^L is the best state indicating there is no network violation, the system is in the healthy state at time t. Otherwise, go to Step 6.

Step 6: The OPF model developed in (11)–(16) is used to evaluate the load curtailment at each BLP at time t. If there exists no load curtailment at each BLP, the system is in the marginal state at time t. Otherwise the system is in the failure state at time t.

Step 7: Go to step 1 if the confidence intervals are not satisfied, otherwise go to Step 8.

Step 8: Calculate the average reliability indices.

The customer and system reliability indices used in the operational phase are the loss of probability at BLP i at time t (LOLP _i (t)), the system loss of load expectation during the operational period T (LOLE(T)) and the system expected energy not supplied during the operational period T (EENS(T)).

These indices can be estimated using the following equations over NS sampling states:

$$ LOLP_{i} \left( t \right) = \sum\limits_{j = 1}^{NS} {X_{j,i} \left( t \right)/N} S $$

(18)

where $X_{{j,i}} (t) = \left\{ {\begin{array}{*{20}l} {\text{0}{\text{ if there is no load curtailment at BLP }}i} \hfill \\ {\text{1}{\text{ if there is load curtailment at BLP }}i} \hfill \\ \end{array} } \right.$

$$ LOLE(T) = \int\limits_{0}^{T} {\left( {\sum\limits_{j = 1}^{NS} {X_{j} (t)/N} S} \right) \cdot \text{d}t} $$

(19)

where $X_{j} (t) = \left\{ {\begin{array}{*{20}l} {\text{0}{\text{ if the system has no load curtailment }}} \hfill \\ {\text{1}{\text{ if the system has load curtailment }}} \hfill \\ \end{array} } \right.$

$$ EENS(T) = \int\limits_{0}^{T} {\left( {\sum\limits_{j = 1}^{NS} {\sum\limits_{i = 1}^{N} {LC_{{j_{i} }}^{{}} (t)} /N} S} \right) \cdot \text{d}t} $$

(20)

where $LC_{{j_{i} }} (t)$ is the load curtailment at BLP i for state j at time t.

The EENS coefficient of variation is used as the criterion for the convergence in the simulation:

$$ \beta_{EENS} = \sqrt {V(EENS(T))} /EENS(T) $$

(21)

where V(EENS(T)) is the variance of EENS(T).

The loss of load frequency (LOLF) is another index used in the reliability evaluation. Usually the LOLF is estimated by non-sequential simulation for long-term reliability evaluation rather than sequential simulation for the operational phase. Reference [27] proposed a method for evaluating the LOLF utilizing the state transition based sequential simulation. The method is based on the basic Markov assumption: system state durations follow corresponding exponential distributions. The LOLF for the operational period T can be assessed as:

$$ LOLF\left( T \right) = \sum\limits_{j = 1}^{NS} {X_{j} \left( T \right)/N} S $$

(22)

where

$$ X_{j} (T )= \left\{\!\! {\begin{array}{ll} 0&\quad {\text{if the system has no load curtailment}} \\ { 1 / {\text{E}}\left( {{\text{D}}_{I} } \right)} &\quad {\text{if the system has load curtailment }} \\ \end{array} } \right. $$

(23)

${\text{E(D}}_{I} )$ is the expected total duration of interruption sequence for the operational period T, which can be evaluated as [27]:

$$ {\text{E(D}}_{I} ) { = }\sum\limits_{j \in J}^{{}} {E (D_{j} )} = \sum\limits_{j \in J}^{{}} {\left( {\frac{T}{{\sum\limits_{j}^{{}} {\lambda_{j} } }}} \right)} $$

(24)

where state j is a failure state in the set of interruption sequence; λ _j is the transition rate between state j and any connected state [27].

The LOLF can provide useful information for system reliability studies. However, the corresponding evaluation is based on the basic Markov assumption including load models, which may not be satisfied in the short term (operational phase) reliability evaluation.

5 System studies

The IEEE-RTS [25] has been restructured to illustrate the proposed techniques. A large wind farm with total generation capacity of 600 MW has been installed in the system. The wind farm consists of 300 Vestas V-80 WTGs with 2 MW rated power [3]. The cut-in, rated, and cut-out wind speeds of a V-80 WTG are 4, 15 and 25 km/h, respectively. Markov model for the output power of a single V-80 WTG and corresponding transition rates are proposed in [3]. In [3], the wind speed series of a wind farm in the northern Iran region is utilized. When the wind speed is below the cut-in speed, the power output of the WTG is zero. When the wind speed is between the rated speed and the cut-out speed, the power output of the WTG is the rated power. When the wind speed is between the cut-in and the rated speed, the power output of the WTG is below the rated power depending on the wind speed. The power output of the WTG was split into 0, 0.5, 1, 1.5, and 2 MW steps in [3]. The transition rates in the Markov model is shown in Table 1, which is obtained from the statistical analysis of wind speed series [3].

Table 1 State transition rates of the WTG (occurrences/h)

The MTTF and MTTR of a WTG are assumed to be 3650 hours and 55 hours, respectively [12]. There are 6 EOGRPs in the system for providing electric energy and reserve. Each of the EOGRPs located at buses 15, 16, 18 and 23 owns one large 575-MW coal thermal generating unit, respectively. The EOGRPs located at buses 13 and 8 have three and one 197-MW oil thermal generating units, respectively. The 575-MW coal thermal generating units are utilized in real life [23], represented as the four-state Markov model. The four oil thermal generators are represented as binary Markov models [11].

The system also has two EFRPs located at buses 1 and 2, which are utilized for providing additional operating reserve. The EFRPs located at buses 1 and 2 have three and two 40-MW gas thermal generating units, which are used as rapid start-up units for providing fast start reserve. Three cases have been studied to analyze the reliabilities for the system and customers under different scenarios. The simulation codes were written in C language and running in a 2.67 GHz Fujitsu laptop.

5.1 Case 1

In the first case, it is assumed that the initial wind speed at the wind farm is 9.5 km/h and the corresponding power output of a WTG is 1 MW, half of the rated power. Suppose the scheduled generated power of the wind farm is 300 MW, which is about 10.5% of the total scheduled power at the beginning of the operating time. The total operating reserve provided by the large thermal generating units is 575 MW, which is equal to the capacity of the largest generator for satisfying the N-1 criterion. All generating units are in a good condition at the beginning of the operating time. The computational time for case 1 running in the 2.67 GHz Fujitsu laptop is 569.6 seconds.

Customers’ LOLP at time t for representative load buses – bus 6 and bus 20 are shown in Fig. 7 and Fig. 8, respectively. It can be observed from Figures that the instant LOLP at each bus is a time variable rather than a constant value. The instant LOLP for bus 6 increases from 0.0215% at t = 1 h to 0.567% at t = 24 h. The instant LOLP for bus 20 increases from 0.0212% at t = 1 h to 0.541% at t = 24 h. In this case, Customers’ reliability at bus 20 is a little higher than that at bus 6 because of a relatively strong transmission network connected with bus 20. Customers’ risk is increasing during the operating period because of the wind power fluctuation and possible random failures of generating units. The system EENS and LOLE are 18.1207 MWh and 0.0883 hours, respectively.

Fig. 7

Customers’ instant LOLP at bus 6 for case 1

Fig. 8

Customers’ instant LOLP at bus 20 for case 1

5.2 Case 2

In the second case, we assume the initial wind speed at the wind farm is 20 km/h and WTGs are generating rated power at time t = 0. In this case, the scheduled generated power of the wind farm is doubled compared with that in case 1–600 MW, which is about 21.1% of the total scheduled power at the beginning of the operating time. Other conditions are the same as those in case 1: The total operating reserve provided by the large thermal generating units is still 575 MW for satisfying the N-1 criterion. All generating units are in a good condition at the beginning of the operating time. The computational time for case 2 running in the 2.67 GHz Fujitsu laptop is 817.9 seconds.

Customers’ LOLP at time t for bus 6 and bus 20 are illustrated in Fig. 9 and Fig. 10, respectively. The instant LOLP for bus 6 increases from 1.8922% at t = 1 h to 39.22% at t = 24 h, which are relatively high values. The instant LOLP for bus 20 increases from 1.8922% at t = 1 h to 39.20% at t = 24 h, which almost has same values as those for bus 6. Therefore, lower customers’ reliabilities are mainly caused by the increasing penetration of fluctuating wind power than the transmission network.

Fig. 9

Customers’ instant LOLP at bus 6 for case 2

Fig. 10

Customers’ instant LOLP at bus 20 for case 2

The system EENS and LOLE are 183.498 MWh and 5.8209 hours, which are about 10 times and 66 times than the values in case 1. Obviously only satisfying N-1 criterion of operating reserve cannot maintain reliability level of power system operation if high penetration of fluctuating wind power has been scheduled.

5.3 Case 3

In the third case, conditions are the same as those in case 2: the scheduled generated power of the wind farm and the operating reserve provided by the large thermal generating units are 600 MW and 575 MW, respectively. For increasing system and customers’ reliabilities, the rapid start-up units owned by the EFRPs have been utilized for providing additional 200 MW operating reserve. The rapid start-up units are committed for operation at t = 1 h. The computational time for case 3 running in the 2.67 GHz Fujitsu laptop is 737.1 seconds.

Customers’ LOLP for bus 6 and bus 20 at time t is illustrated in Fig. 11 and Fig. 12, respectively. As shown in Fig. 11, the commitment of rapid start-up units decreases the LOLP for bus 6 from 1.881% at t = 1 h to 0.0189% at t = 2 h. Customers’ LOLP for bus 6 at t = 24 h is 0.6895%, which decreases about 98.2% compared with that in case 2. The instant LOLP for bus 20 has the almost same pattern and values as those for bus 6. The system EENS and LOLE are 20.97 MWh and 0.0996 hours, which decreases about 88.6% and 98.3% compared with those in case 2.

Fig. 11

Customers’ instant LOLP at bus 6 for case 3

Fig. 12

Customers’ instant LOLP at bus 20 for case 3

6 Conclusions

In the last four decades, reliability evaluation techniques and reliability management strategies have been well developed and studied. These reliability evaluation techniques are more focused on planning and expansion of conventional power systems. However, the fast development and widely utilization of intermittent and fluctuating wind power generation have brought complexities for securing system balancing and maintaining system and customers’ reliabilities during the operational phase. Moreover, in the last two decades, power systems have been restructured: electric energy and reserve are traded in different correlated markets. The restructuring of power systems has changed reliability management strategies fundamentally. Some existing and widely used criteria e.g., N-1 criterion may or may not be suitable for securing the reliable operation of power systems. In this paper, a new technique for assessing operational reliabilities of restructured power systems with high wind power penetration has been developed, which is based on reliability network equivalents and time-sequential simulation approaches. For reducing computational complexities, a simplified method has been developed and utilized in the simulation procedure. The proposed technique can be used to assistant system operator and market participants to assess their risks during system operation and make optimal decisions.