Introduction

Heterogeneity in cancer cell phenotypes enhances the population’s capability of resisting fluctuating adverse environments1,2,3, like those produced by the administration of drugs and anticancer treatments4. In particular, recent works suggest that size heterogeneity specifically impacts cancer fitness. However, the exact relationship between size and disease is poorly understood, as much as the strategies cancer cells adopt to create and maintain such heterogeneity5. At a mechanistic level, cell size is determined by the combination of homeostatic processes operating at different timescales. If on shorter timescales, size is set by the capability of cells to regulate processes like water entry, membrane trafficking, and protein synthesis; on longer timescales, size results from the interplay between cell growth and division6. As a result, under steady-state conditions, isogenic populations tend to maintain cell sizes around typical7, type-specific mean values, although significant cell-to-cell variability is often observed8. Indeed, observed size distributions span over an order of magnitude9, usually display lognormal shapes and are characterized by coefficients of variation (CVs) of 0.1–0.35,10. Such cell-to-cell variability in clonal cell populations is ultimately linked to the inherently stochastic nature of molecular processes, which reflects in fluctuations of the production/degradation of cellular constituents and noisy partition of cell content/volume during cell division11,12,13,14.

Studies on bacteria and yeast populations showed that size distribution homeostasis can be obtained by modulating the amount of growth produced during the cell cycle in such a way that on average larger cells at birth grow less than small ones. The strategies that cellular populations may adopt to reach and maintain such size homeostasis have been roughly classified into three distinct models, depending on whether divisions occur after a certain time (timer), upon reaching a certain size (sizer), or after the size of the cell has increased by a finite volume (adder).

In particular, a phenomenological linear relation (usually referred to as stochastic map) has been observed between the size at birth (sb) and the size at division (sd)15: sd = asb + η, where η represent noise derived from the specific biological size control model, while the slope, a, defines the size control models. Usually, experiments look at the quantity, \({{\Delta }}=\left\langle {s}_{d}\right\rangle -\left\langle {s}_{b}\right\rangle =(a-1)\left\langle {s}_{b}\right\rangle +\left\langle \eta \right\rangle\). So that, for a = 2, the size at division is directly proportional to the size at birth. This mechanism is referred to as a timer model, hypothesizing that the cell size is controlled by a cell cycle timer that sets a time limit for the growth phase, and once the time limit is reached, the cell divides. Intuitively, if cell size growth is exponential such a mechanism will end up in big cells to proliferate faster than small cells thus producing a divergent size variance. Only a linear size increase under specific constraints on division symmetry is compatible with this homeostatic strategy16. For a = 1, a certain volume < η > is added before division, which is uncorrelated to the initial size. This behavior has been proposed for various populations of bacteria, cyanobacteria, and budding yeast populations17,18. Finally, if a = 0, the size at division is completely set by the stochastic term, which is called a sizer mechanism. The sizer model suggests that the cell size is determined by a threshold size, and once the cell reaches this threshold size, it triggers the cell division process. Sizer-like mechanism has been found for organisms such as the fission yeast S.Pombe19,20,21.

To determine which model is followed by the different kinds of cell types and determine the cell size distribution in both bacterial and eukaryotic cell populations, various experimental techniques have been developed22,23, comprising time-lapse microscopy24, single-cell tracking25, and gene tagging26.

For instance, ref. 27 used fluorescence microscopy united with a mathematical framework, showing that it is possible to get dynamical information from fixed cells and revealing feedback linking between cell growth and cell cycle. Sung and coworkers developed a phase microscopy technique for highly accurate measurements of cell mass in adherent mammalian cells28.

Parallel to experimental progress, different models of cell size regulation (with few key parameters) have been proposed. From the pioneering works of Powell29 and Anderson30, that compared analytical predictions with cell counts experiments to more recent works that proposed mathematical models to interpret both population and single cell-based data17,31,32,33,34,35,36,37,38,39.

In particular, progress in the quantitative measurement of single-cell features, using, for instance, mother machines, allows for the characterization of the growth and division strategy for fast-proliferating cell populations, like bacteria and yeasts (whose doubling times are on the order of hours). For other cell types, like mammalian ones, it is harder to track several divisions due to lower division rates and more stringent growing conditions. A work by ref. 40 investigated a wide spectrum of mammalian cell types combining a microfluidic system with real-time cell imaging to find different adopted homeostatic strategies, ranging from quasi-timers to size-like ones. Varsano et al.41 studied the growth of leukemic basophils and macrophages finding that smaller cells follow a size-like division strategy while average cells behave more like adders.

In this paper, we propose an experimental protocol coupled with a minimal mathematical model to determine the homeostatic strategy adopted by populations of leukemia cells that does not rely on cell imaging data. In particular, the experimental protocol, we propose, makes use of flow cytometry measurements which yield information on the cell size (via the collected forward scattering signal42) and permit (via live cell fluorescent tags14) the determination of cell lineage and partition noise. Experimental data are compared with the predictions of a minimal model where the variation of a single parameter allows the exploration of the different size-homeostasis strategies. In particular, we developed a quantitative analytical framework based on three key features: (i) cell growth and division rates depend on powers of the cell size, (i) cell division can take place after the cell accomplishes a certain number of intermediate tasks, and (iii) daughter cells can inherit an uneven portion of the mother cell size.

We show that: (i) using forward scattering as a proxy for cell size43 allows us to observe the dynamics of cell size distributions, which are in qualitative agreement with those shown by both numerical simulations of agent-based systems and a minimal analytical model based on a population balance equation. (ii) A simple exponential distribution of division times can not reproduce the observed dynamics, which instead requires an Erlang distribution with at least the sum of three independent exponentially distributed intermediate times. Finally, (iii) stratifying data according to cell generations allows us to fully infer the division strategy adopted by leukemia cells.

Results

Experimental protocol

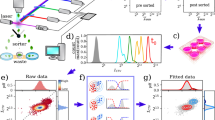
To measure the cell size distribution and follow its dynamics, we developed a protocol based on flow cytometry measurements. Extending the procedure we previously proposed to measure the partition noise of cellular compounds14, we made use of CellTrace-Violet (CTV), a fluorescent dye, to mark cell cytoplasm (see Method section) and follow the proliferation of the population by looking at the dynamics of the fluorescence and forward scattering signals in time via a series of flow cytometry measurements. As depicted in Fig. 1 and explained in more detail in the Methods, marked cells are first sorted (see panel a), so that an initial population with a narrow CTV distribution is selected (Fig. 1b). The sorted population is then collected and cultured in standard growth conditions (see Methods). Samples of the population are collected at different times during the cell proliferation, recording CTV, forward FSC, and side scattering SSC, intensities for each analyzed cell (see Fig. 1c). SSC and FSC are used to define the viable population at each time point (see Supplementary Fig. 5 for details). Figure 1d shows the evolution of the distributions of \({\log }_{2}\) CTV fluorescence intensities. The purple curve (low-right corner of the panel) corresponds to the post-sorting distribution, which is considered the time zero of the dynamics. Looking at the CTV intensity at different times during the proliferation of the cell population, one observes a progressive shift of the initial fluorescence and the appearance of multiple peak distributions. As CTV homogeneously binds to cytoplasmic proteins, upon division, the fluorescence of each mother cell is divided into the two daughters as a result of the cell division process. Each division produces two daughters, thus on average the CTV distribution of the daughter cells has half the mean fluorescence of the mother distribution (see inset in Fig. 1d).

Fig. 1: Experimental protocol.
figure 1

a Schematic representation of a fluorescence-activated cell sorter (FACS) working principle. Stained cells pass one at a time in front of a laser source that excites the fluorophores of the markers. The forward scattered (FSC), and side scattered (SSC) light, together with the one emitted by the dye fluorophores is collected and analyzed. Eventually, a sorter divides cells according to certain thresholds on the measured intensities. b SSC vs FSC intensities for the initial population of marked cells together with the distribution of CTV (CellTrace Violet, cytoplasm marker) intensity. c Schematic representation of the time course protocol: the initial sorted population is kept in culture (see Methods) and samples are collected at different time points and analyzed via a flow cytometer that collects both FSC, SSC, and CTV intensities for each analyzed cell. d Time evolution of the population CTV fluorescence intensity. Colors from purple to dark green represent different time points along the experimental time course, from time zero to 72 h. Inset shows the mean fluorescence as a function of the population generations. e Density distribution of the forward scattering intensity of the cell population at different times. Colors range from purple to dark green as the time goes from zero (sorting of cells, i.e., start of the experiment) to 90 h.

Full size image

Parallel to the evolution of the CTV intensity, we track the evolution of the FSC intensity. As it can be seen from Fig. 1e, the distribution shifts toward higher values than those presented at the initial time point (purple curve), while its variance increases. This behavior can be explained by recalling that the initial population is sorted, consequently, its size distribution is out of equilibrium.

Forward scattering evolution probes cell size dynamics

To identify the different generations from the CTV intensity profiles, we applied a fitting protocol via a Gaussian Mixture Model of the form: \(P(\ln x)={\sum }_{g}{w}_{g}N(\ln x,{\bar{x}}_{g},{\sigma }_{g})\) combined with an Expectation Maximization algorithm (see Methods for details). An example of the result of the fitting procedure is shown in Fig. 2a. From left to right, the distributions of the log2 of the CTV intensity for different time points are shown in gray, while the Gaussian distributions obtained as best fits of the experimental data are reported in different colors corresponding to the different identified generations. Together with the mean and variance of each Gaussian, the fitting procedure yields the probability of each cell to belong to the various identified generations. Since for each cell, both CTV and FSC signals are measured at each time point, we can use the information coming from the GM procedure to identify the subpopulations corresponding to different generations from the FSC distributions. Figure 2b displays the FSC intensity distributions of the same population from which the CTV distributions (shown in panel a) were measured. In this case, gray curves mark the total population, while colored ones correspond to the different generations. Comparing the distributions of the same generation in different snapshots, one notes that newer generations have distributions shifted toward smaller FSC values with respect to older ones. In particular, the distributions (dots) of the grand-daughter cells are reported in Fig. 2c, together with the best fits of a normal distribution for each distinct time point. Mean and variance as a function of the snapshot times are reported in Fig. 2d. Finally, we evaluate the Pearson correlation coefficients between CTV and FSC intensities as a function of time (Fig. 2e). Results show that the correlation is null just after the sorting procedure and then reaches a high positive value (around 0.6) in the next snap times. This behavior appears reasonable since cytoplasm volume scales with the cell size; on the other hand, an almost zero correlation after sorting may indicate that the rates of CTV uptake are moderately dependent on cell size.

Fig. 2: Analysis of forward scattering and CTV intensity data.
figure 2

a Density distribution (gray curves) and best fit of a Gaussian Mixture Model (colored curves) of the CTV fluorescence intensity measured in a Jurkat population at different times during its proliferation. From left to right, snapshots at 0, 19, 23, 27, and 43 h from the CTV staining process. Curves colored from blue to purple are ordered according to the identified generations. b Same as in (a) but for the measured FSC intensities. The colored curve highlights the subpopulations corresponding to the different generations that have been identified thanks to the Gaussian Mixture model fitting of the CTV intensities. Intensities have been rescaled by a factor of 105. c Density distributions (dots) and best normal fit (lines) of the rescaled forward scattering intensity of the granddaughter’s cells (second generation) measured at different times during the proliferation of the population. The values of the R2 for each fit are reported in the figure legend. d Mean and variance of the size of the grand-daughter subpopulation as a function of time. Size is quantified by the rescaled FSC intensity. Marker sizes are comparable with the Standard Error over the Mean and Variance of each time point. e Pearson correlation coefficient of CTV and forward scattering intensities for the snapshots.

Full size image

Minimal model for size dynamics

In single-cell size measurements, the division strategy can be directly assessed by looking at the slope of the linear relation between birth and division sizes of the cells. In our framework, to infer the control strategy, we compared data with a theoretical framework that accounts for the time evolution of the cell size distribution under different possible growth and division regimes, i.e., different size-homeostasis strategies.

Exponentially distributed division times

To allow for a comparison, we aimed at modeling the growth and division dynamics of a population of cells growing in a controlled environment. We assumed that each cell of the population is thus characterized by a size, s, which changes in time as the cell grows and divides, and by its generation, g.

Assuming balanced exponential growth of the population and referring to ng(s(t), t) as the number of cells in the population having size s at time t and having divided g times, this number will evolve in time according to:

$$\frac{\partial {n}_{g}(s,t)}{\partial t} +\frac{\partial \left(g(s)\cdot {n}_{g}(s,t)\right)}{\partial s}=-\gamma (s){n}_{g}(s(t),t)+\\ +2\int_{0}^{\infty }d\eta \,\gamma (\eta )\,\phi (s| p\eta )\,{n}_{g-1}(\eta ,t)$$
(1)

where g(s) and γ(s) are the size-dependent growth and division rate, respectively, and ϕ(x∣py) quantifies the probability that a daughter cell inherits a fraction p of mother cell size y. See Supplementary Note 1 for the derivation of Eq. (1).

Along the lines of previous works31,33,37,44, we assumed that both growth and division rates are given by power of the cell size, i.e., we assumed \(g(s)=\frac{ds}{dt}=\lambda {s}^{\alpha }\) and γ(s) = κsβ. As shown by ref. 45, with this minimal assumption it is possible to recover all main size-homeostatic strategies tuning the parameter ω = β − α.

Note that we refer to linear/exponential growth considering the single-cell growth rate, ds/dt, which is linear for α = 0 and exponential for α = 1. We make the approximation that the growth rate expression remains the same independently from the cell cycle state (see for example in ref. 46). For what concerns the growth of the population in terms of the number of cells as a function of time, we assume that the population is in balanced exponential growth as previously stated.

If we now look at the variation of the total number of cells at generation g, we have:

$${\dot{N}}_{g}=\frac{d}{dt}{N}_{g}(t)=\int_{0}^{\infty }\frac{\partial }{\partial t}{n}_{g}(s,t)ds$$
(2)

which can be recast as

$${\dot{N}}_{g} = \int\,ds\left[-\frac{\partial }{\partial s}\left(\lambda {s}^{\alpha }{n}_{g}(s,t)\right)-k{s}^{\beta }{n}_{g}(s,t)+\right.\\ + 2k\int\,d\eta {\eta }^{\beta }\int\,ds\phi (s| p\eta )\,{n}_{g-1}(\eta ,t)$$
(3)

The first term of the integral goes to zero thanks to the fact that either the size or the number of cells is zero in the integration extrema; thus the above equation becomes:

$$\frac{{\dot{N}}_{g}}{{N}_{g}}=-k \, {\left\langle {s}^{\beta }\right\rangle }_{g}+2k \, {\left\langle {s}^{\beta }\right\rangle }_{g-1}\frac{{N}_{g-1}}{{N}_{g}}={{{\Phi }}}_{g}$$
(4)

where < x > g = ∫ dsxρg and we introduced the probability of finding a cell with size s at time t and generation g as

$${\rho }_{g}(s,t)=\frac{{n}_{g}(s,t)}{{N}_{g}(t)}.$$
(5)

The fraction Ng−1/Ng is difficult to be experimentally measured. Thus, we want to recast it in a more handy form. To do so, we define the fraction of cells belonging to a certain population at each time as:

$${P}_{g}(t)=\frac{{N}_{g}(t)}{{\sum }_{q} \, {N}_{q}(t)}$$
(6)

Eq. (4) can be used to compute the dynamics of the fractions, Pg. In fact, we have that3:

$$\dot{{P}_{g}}=\left(\dot{\frac{{N}_{g}(t)}{{\sum }_{q} \, {N}_{q}(t)}}\right)=\frac{\dot{{N}_{g}}}{{\sum }_{q} \, {N}_{q}}-{P}_{g}\frac{{\sum }_{q} \, \dot{{N}_{q}}}{{\sum }_{q} \, {N}_{q}}$$
(7)

which, after some calculation, can be expressed as:

$$\dot{{P}_{g}} = -k \, {\left\langle {s}^{\beta }\right\rangle }_{g}\,{P}_{g}+2k \, {\left\langle {s}^{\beta }\right\rangle }_{g-1}\, {P}_{g-1} + \\ + {P}_{g}\sum\limits_{q}\left(k \, {\left\langle {s}^{\beta }\right\rangle }_{q}\,{P}_{q}-2k \, {\left\langle {s}^{\beta }\right\rangle }_{q-1}\, {P}_{q-1}\right)$$
(8)

It remains to obtain expressions for the mean and variance dynamics. Again, we can start from Eq. (4). In fact,

$$\dot{{n}_{g}}=\dot{{N}_{g}}\rho +{N}_{g}\dot{{\rho }_{g}}$$
(9)

and

$$ - \frac{\partial }{\partial s}\left(\lambda {s}^{\alpha }{n}_{g}(s,t)\right)-k{s}^{\beta }{n}_{g}(s,t)+\\ + 2k\int\,d\eta {(\eta )}^{\beta }\,\phi (s| p\eta )\,{n}_{g-1}(\eta ,t)=\\ = {{{\Phi }}}_{g}{N}_{g}{\rho }_{g}+{N}_{g}\dot{{\rho }_{g}}\,.$$
(10)

Reordering and dividing by N, we get

$$\dot{{\rho }_{g}} = -{{{\Phi }}}_{g}{\rho }_{g}-\frac{\partial }{\partial s}\left(\lambda {s}^{\alpha }{\rho }_{g}\right)-k{s}^{\beta }{\rho }_{g}+\\ +2k\int\,d\eta {\eta }^{\beta }\,\phi (s| p\eta ){\rho }_{g-1}(\eta ,t)\frac{{N}_{g-1}}{{N}_{g}}\,.$$
(11)

Without loss of generality, one can express ϕ as

$$\phi (s| p\eta )=\int_{0}^{1}dp\,\pi (p)\delta (s-p\eta )$$
(12)

where π(p) is a general probability function of the fraction of inherited cell size.

Thanks to Eqs. (11) and (12), we can easily compute the distribution moments evolution equations as:

$${\left\langle {\dot{s}}^{i}\right\rangle }_{g}= \lambda \cdot i\cdot {\left\langle {s}^{(\alpha +i-1)}\right\rangle }_{g}-{{{\Phi }}}_{g}{\left\langle {s}^{i}\right\rangle }_{g}-k \, {\left\langle {s}^{(\beta +i)}\right\rangle }_{g}+\\ +2\,k\,{\left\langle {p}^{i}\right\rangle }_{\pi }{\left\langle {s}^{(\beta +i)}\right\rangle }_{g-1}\frac{{P}_{g-1}}{{P}_{g}}$$
(13)

where < pi > π refers to the i-th moment of π(p) (see Supplementary Note 7 for details on how the last term is obtained).

Erlang distributed division times

Assuming size-dependent growth and division rates end up producing exponentially-distributed division times33, while it has been previously shown how intergeneration division time statistics is better captured by Erlang distributions33,47. To retrieve an Erlang-like distribution, we introduce a series of intermediate states, the cell has to go through, before starting the division as done for instance by ref. 45 to describe E. coli size dynamics. Each of the state’s duration has an exponential distribution of times. Introducing another index accounting for the intermediate states the cell transit in before division, and repeating all calculations (see Supplementary Notes 4, 5), one ends up with:

$${\left\langle {\dot{s}}^{i}\right\rangle }_{g,q} = \,\lambda \cdot i\cdot {\left\langle {s}^{(\alpha +i-1)}\right\rangle }_{g,q}-{{{\Phi }}}_{g,q}{\left\langle {s}^{i}\right\rangle }_{g,q}-k \, {\left\langle {s}^{(\beta +i)}\right\rangle }_{g,q}+\\ +k \, {\left\langle 2\,{p}^{i}\right\rangle }_{\pi }^{{\delta }_{q,0}}{\left\langle {s}^{(\beta +i)}\right\rangle }_{g,q-1}\frac{{P}_{g,q-1}}{{P}_{g,q}}$$
(14)

where \({\left\langle \cdot \right\rangle }_{g,q}\) stands for the statistical average over ρg,q, the density of cells that divided g times and passed q-th out of Q intermediate states and δi,j is the Kronecker delta. Similarly, the fraction of cells being at generation g and state q evolves according to

$$\dot{{P}_{g,q}}= -k \, {\left\langle {s}^{\beta }\right\rangle }_{g,q}{P}_{g,q}+2k \, {\left\langle {s}^{\beta }\right\rangle }_{g,q-1}{P}_{g,q-1}+ \\ +{P}_{g,q}\sum\limits_{h,w}\left(k \, {\left\langle {s}^{\beta }\right\rangle }_{h,w}{P}_{h,w}-{2}^{{\delta }_{w,0}}k \, {\left\langle {s}^{\beta }\right\rangle }_{h,w-1}{P}_{h,w-1}\right)$$
(15)

for q > 0, and

$$\dot{{P}_{g,0}}= -k \, {\left\langle {s}^{\beta }\right\rangle }_{g,0}{P}_{g,0}+k\, {\left\langle {s}^{\beta }\right\rangle }_{g-1,0}{P}_{g-1,0}+\\ +{P}_{g,0}\sum\limits_{h,w}\left(k \, {\left\langle {s}^{\beta }\right\rangle }_{h,w}{P}_{h,w}-{2}^{{\delta }_{w,0}}k \, {\left\langle {s}^{\beta }\right\rangle }_{h,w-1}{P}_{h,w-1}\right)$$
(16)

otherwise.

Equations (14) and (15), (16) fully describe the dynamics of the cell population, however except for some specific sets of parameters, this set of equations is not closed; in fact, the time derivative of the i-th moment may contain higher moments depending on the values of α and β. Indeed, the set is closed only in the case of a division rate that does not depend on the cell size (i.e., β = 0). To solve the system in the general case, we must choose a moment closure strategy. To do so, we exploit our findings on the FSC distributions stratified by generations44. In fact, the latter are well fitted by normal distributions, showing that our experimental resolution on the real generation size distribution can at best be on the second moment. Considering additional moments, one would risk inserting experimental noise in place of real signal, while restraining only to the evolution of the first two moments assures considering the less unbiased statistics from a maximum entropy viewpoint48,49.

Thus, we assume that the single generation size distributions have normal moments (note that this is not the case of the total population size distribution, which shows a log-normal distribution instead) and opt for a normal moment closure (see Supplementary Note 6 for details).

To validate the obtained relations and test the adopted moment closure, we compare the solution of the differential equations with the results of stochastic simulations of an agent-based model, where an initial population of cells grow and divide following the same grow and division rates functional form used in Eq. (1). To associate at each cell a proper division time, a Gillespie procedure has been adopted. See the Method section for a detailed description of the stochastic simulation protocol. The outcomes of the simulations are recapitulated in Fig. 3. In particular, Fig. 3a provides a schematic representation of the life cycle of a single agent, i.e., cell in the population: a cell is born with initial size, sb; it grows according to a certain growth rate, g(s), for a certain set of times, \({{\tau }_{q}}_{0}^{Q}\), which encode a series of independent intermediate states the cell has visited before actual division (see Supplementary Note 5). From a biological point of view, such states can be linked to the phases of the cell cycle. Upon reaching the division size, sd, the mother cell splits into the two daughter cells, one inheriting a fraction p of the mother volume and the other keeping the remaining 1 − p fraction.

Fig. 3: Model of size-homeostasis.
figure 3

a Schematic representation of cell growth and division. A mother cell with starting size sb grows up to a size sd and then splits into two daughter cells whose starting sizes are fractions of the mother cell size. b Probability density distribution of the division times, τd as a function of the number of intermediate states a cell must visit before dividing. Time spent in each of the intermediate states is assumed to be exponentially distributed. c From left to right, schematic representation of the sizer, timer, and adder mechanisms: cells grow (i) until a certain size is reached, for a certain time interval, or until a determined amount of size is added to the starting one. d Rescaled difference between size at division and birth, Δ = sd − sb vs rescaled birth size for the three size-homeostasis models. Both quantities are rescaled by the respective mean values. Light green dots represent the values obtained via a numerical simulation of a cell population in each regime, while orange, red, and blue dots a obtained binning over the x-axis. e Fraction of cells having divided g times since the initial time of the simulation as a function of simulation time. From left to right, cells grow and divide according to a sizer, timer, or adder strategy, respectively.

Full size image

To begin with, we verified that such a framework reproduces the expected sizer, timer, and adder (see Fig. 3c, d) behavior upon varying the ω = β − α parameter. Indeed, simulations with α = 1 and β taking values 2, 0, or 1 produced the expected trend for the sizer, timer, and adder, respectively. Next, we compared the solution of the model, in the normal closure approximation, with the results of the agent-based stochastic simulations. In Fig. 3e, we show the results for the fractions of cells found in different generations as a function of time. The good agreement, measured by the R2 of ~ 0.9, suggests the choice of the moment closure provides a good approximation for such kind of dynamical process.

Model parameters govern distinct and measurable aspects of cell dynamics

The derived framework depends on several parameters, thus, we next proceeded to characterize the role of the different model parameters and their effects on the quantities we can measure experimentally, i.e., the population size distribution moments, their per-generation stratifications, and the relative abundances of cells in different generations during the dynamics.

At first, we focused on the mean size of the whole population. Measuring the mean FSC as a function of time for populations sorted with three different values of initial mean size, we found that they eventually reached comparable values of the mean size within the first 24 h of the experiment (see Fig. 4a). Comparing the trend shown by experimental data with those of the model (Fig. 4b1, b2), we found that the asymptotic mean size is not a function of the starting mean sizes (see Fig. 4b1) but it is modulated by the ratio of the rate coefficients, λ/κ. In particular, Fig. 4b2 clearly shows that the higher the ratio λ/κ, the higher the population mean size in the long time limit. Looking at the trend of the Coefficient of Variation, CV, instead, we found that the size of the Jurkat population displays a CV with an oscillating behavior around a value of about twenty-three percent as shown in Fig. 4c. A comparison with the model trends again shows that this behavior is qualitatively reproduced by the model. Moreover, the key parameter modulating the variance of the cell size distribution is the exponent of the division rate, β. In particular, the higher the exponent the lower the fluctuations of the cell sizes (see Fig. 4d2).

Fig. 4: Role of the model key parameters.
figure 4

a Mean of the rescaled size distribution, < s > as a function of time for three Jurkat cell populations that have been sorted for low, medium, and high values of forward scattering intensity at time zero. b1 Mean size of the population as a function of time obtained solving Eqs. (13) for different values of the mean size of the population at time zero, < s(0) > . b2 Same as in (b1) but for different values of the ratio λ/κ. c Same as in (a) but for the Coefficient of Variation, CV. d1 Same as in (b1) but for the CV. d2 Same as in (d1) but varying the division rate exponent, β. e Fraction of mother (blue), daughter (green), or granddaughter (red) subpopulations as a function of time. The maximum observed fractions of cells for the three different generations are reported in the figure inset. Maximum values are computed fitting the mother fraction with a sigmoidal function, while daughter and gran-daughter ones are fitted with two normal distributions. Expected maximum fractions obtained solving Eqs. (14) for different numbers of intermediate tasks are shown in shades of purple. Maxima increases as a function of Q. f Fraction of cells belonging to different generations as a function of time obtained solving Equations (14) for different levels of partition noise. The fraction of inherited volume, p, is described by a normal distribution centered in 1/2 and with different variances as shown in the inset. In all panels reporting experimental data, when not displayed, bars are smaller than the size of the point dots.

Full size image

To explore the role of the remaining model parameters, i.e., the number of intermediate states and the division noise, we moved to consider the time evolution of the fractions of cells per generation. Figure 4e shows the results for three timecourses as dots. As one can see, experimental data exhibit a trend qualitatively similar to those obtained by solving Eqs. (8) and shown in Fig. 3e. Notably, the maximum fraction of observed first-generation cells in the population is 0.85 ± 0.05. This value is not compatible with a single-task model of cell growth and division but requires a cell division time given by the sum of at least three independent exponentially distributed times. Indeed, this can be seen comparing the predicted maximum fraction of daughter cells obtained by solving Eqs. (8). The inset in Fig. 4e displays the maximum fraction values obtained by changing the number of states, Q, from one to 6. Finally, we quantified the role of division noise in terms of the shapes of the generation fractions curves. As discussed in the previous sections, given the high correlation between FSC and CTV intensity, we assume that the size at division follows the same statistics of the cytoplasmic components. In previous work, we found that Jurkat cells partition their cytoplasm symmetrically14. Thus, we assumed that even the fraction of inherited volume is a random variable with a normal distribution, centered in 1/2 and having a certain variance, \({\sigma }_{p}^{2}\) (see inset in Fig. 4f). Solving the model equations with different values of σp while keeping all other parameters fixed gives the trend reported in Fig. 4f. It can be seen that the higher the level of division noise, the more the maximum fraction of cells per generation decreases, while the same generation tends to endure for longer times, i.e., smaller cells can be produced that require longer times to divide. Note that this reflects an increase in the total population variance.

Size dynamics behaves according to a size-like homeostatic strategy

Finally, we compared the prediction of the model against the collected data. To begin with, we checked that the proliferation of the population of Jurkat cells was in a balanced exponential regime. In particular, we studied the behavior of the logarithm of the number N of live cells per ml (normalized by the initial density) versus time, which defines the growth curve of the population23. As one can see from Supplementary Fig. 1, data are compatible with an exponential trend after an initial lag phase of approx. 7.5 h (green dotted line in Figure). The obtained doubling time of 19 ± 3 h is in accordance with literature data on the same cell type50.

Next, we proceeded to find the best values of the model parameter able to reproduce the observed experimental trends. As discussed in the previous section, Eqs. (13) and Eqs. (8) depend on four parameters governing the growth and division rates, two parameters fixing the first two moments of the initial size distribution, the number of intermediate tasks, Q, and the variance of the inherited size fraction. In particular, the mean and variance of the initial size distribution are directly measurable from the starting post-sorting forward scattering distribution, while the exponent of the growth rate is fixed to 1, as required to reproduce the exponential growth dynamics compatible with the trend of the variance evolution of the mother cell size variance. Note that we re-scaled forward scattering intensities by the mean of the starting population to work with smaller numbers. Figure 5 shows the results of the best fit between the experimental data and the model. In particular, we minimized the cost function defined as the squared sum of the residues of the fractions of cells in the different generations (Fig. 5a) via Approximate Bayesian Computation Sequential Monte Carlo (ABC SMC) for parameter estimation51. As the model depends on 5 free parameters, we opted not to include size distribution moments information in the cost function to use them as an independent validation in the selection of the best growth model. Best fit curves are obtained with the parameters: κ = 0.016 ± 0.007, λ = 1.29 ± 0.03,β = 6 ± 1, Q = 5 ± 1, and \({\sigma }_{p}^{2}=0.003\pm 0.001\).

Fig. 5: Model vs experimental data.
figure 5

a Measured fractions of cells in different generations as a function of time (dots) and curves given by the best fit of the minimal model, described by Eqs. (13) and Eqs. (8). b1, b2 Same as in (a) but for the mean re-scaled total size and its CV given by the forward scattering measurements. c Mean rescaled size for different generations as a function of time (dots) and trends given by the best-fit solution of the model (lines). d Square root of the variance of the rescaled size for different generations as a function of time (dots) and trends given by the best-fit solution of the model (lines). In all panels reporting experimental data, bars are smaller than the size of the point dots.

Full size image

As one can see from Fig. 5, the parameters of the fit best reproduce the dynamics of mean and variance of the size distribution for both the total population and the single generations (as also testified by the values of the R2). Supplementary Fig. 3 shows the outcome of the ABC SMC for a parameter set having β = 1, i.e., compatible with a perfect adder strategy, which, while providing good trends for the population fractions, has a poorer agreement on the size moments behaviors.

Notably, the optimal value of the β exponent of the cell division rate is equal to 6, which indicates a near-adder strategy for size homeostasis. Note that in the proposed model, a β of 1 would have indicated a perfect adder strategy, while β → ∞ is a perfect size sensing.

Discussions

Cell size is a phenotype that exhibits a huge variability across different kinds of cells. Typical sizes of bacteria span a range of 1–10 μm, eukaryotic cells have linear sizes of 5–100 μm, to end at neuronal cells whose size is up to some meters. Besides such inter-kind size heterogeneity, cells of isogenic populations have a well-defined typical size52, that influences and is influenced in return by processes such as transcription, translation, and metabolism53,54, as cell volume and surface area affects molecule reactions and nutrient exchanges55. How this typical size is preserved despite the complex and noisy machinery56,57 of cellular processes that are at play in proliferating cells, is a question that remains still largely unanswered7, especially for cancer cells that have ten-fold slower proliferation timescales than bacteria or yeast cells.

Over the years, several models have been proposed to explain how cells regulate their size. These models provide insights into the molecular mechanisms that govern cell growth and division and help researchers identify key regulatory pathways that could be targeted for therapeutic purposes. In particular, (i) cells that divide after a certain time from birth are said to follow a timer process; (ii) if division takes place when the cell reaches a certain size one speaks of the sizer model; while (iii) an adder mechanism consists in adding a certain volume which does not depend on the birth size.

The ‘canonical’ way to assess the size homeostatic strategy adopted by a certain cell type is based on the trend shown by the size at birth vs that at division. To obtain such a relation, one has to follow the proliferation of single cells and measure the size of the same cell at its birth and just after its entry into the mitotic phase. While such a procedure provides a reliable way to determine the homeostatic behavior and a sure way to track cell lineages, it also has the limitation of measuring the birth and division sizes, i.e., following the dynamics of individual cells, which in turn limits our understanding of size determination mechanisms in cancer5,58. To address such problems, we sought an alternative/complementary procedure able to provide high statistics while preserving cell growth conditions. We propose an experimental protocol that does not explicitly consider birth and division size but instead utilizes flow cytometry data in combination with a minimal mathematical model to determine the growth and division mechanism of Jurkat cancer T-cells.

Our main finding is that a model based on power functions of the size for division and growth rates successfully reproduces the key features of Jurkat cell size dynamics, including an Erlang distribution of division times, a size-like strategy, and the presence of fluctuations in the inherited size fraction between daughter cells.

In particular, analyzing the maximum fraction of cells found in the first generations, we found that for the model to correctly reproduce observations, cell division time has to be given by the sum of a minimum of three independent and exponentially distributed intermediate times. This is in accordance with the evidence Chao and coworkers provide of the human cell cycle as a series of uncoupled, memory-less phases59. Our protocol proved effective in detecting the dynamics of the size also among the different cell cycle phases, thus it would be possible to further investigate these aspects in the future.

Notably, our prediction of a size dependence in the division rate of leukemic T-lymphoblast is in accordance with the findings of ref. 60 who showed that growth rate is size-dependent throughout the cell cycle in lymphoblasts.

Other studies considering leukemia cells concluded that small leukemia cells behave as a sizer, while average-size cells follow an adder model41. Using a combination of microfluid and cell imaging, ref. 40 assessed the division model for a wide range of cell types, finding that Raji cells, a suspension lymphoblast-like cell line follow a timer-like division model while mouse leukemic L1210 cells, a line exhibiting lymphoblast morphology set in the adder-sizer region. We note that the partial accordance with previous investigations may rely on biological differences between the considered cells or in the different used methods.

Finally, we measure the division noise as CTV noise through correlation analysis, finding that the shapes of the generation fraction curves were compatible with a symmetrical division with fluctuations around the mean up to ten percent, which is in agreement with the fluctuations observed in another line of leukemic lymphoblast by ref. 28 via accurate phase microscopy experiments.

The model we present is not limited to exponential growth, a major assumption in most of the analytical modelizations present in literature37. In fact, while this common assumption holds for various cell types, it is not universal. For example, Schizosaccharomyces pombe (fission yeast) is a case where the increase of cell size with time after birth is non-exponential61,62.

We note that our results depend on both the generation fractions and the FSC signal. While fraction signals are reasonably solid, the forward scattering can only be considered as a proxy for cell size, thus future works should focus on finding a better descriptor. In this respect, possible replacement may come from novel Neural Network-based approaches that use full scattered light to get a more precise estimate of the cell size see for instance ref. 63 or fixed-cells dyes, like succinimidyl ester dye, SE-A647, that provides a good measure of cell mass27.

From the analytical point of view, the derived exact expressions for the size moments and the population fractions evolution could be further expanded to account for fluctuations in the key parameters (e.g., κ and λ), and to combine different strategies in different tasks should be performed.

In conclusion, we proposed an experimental and theoretical apparatus to characterize the growth and division of leukemia cells. We found that (i) while following a size-like homeostatic strategy, Jurkat cells (ii) need to pass a certain number of intermediate states before dividing, which are independent and exponentially distributed. (iii) Experimental data are well reproduced by a minimal model that depends on relatively few, physically meaningful parameters.

Methods

Cell culture

E6.1 Jurkat cells (kindly provided by Dr. Nadia Peragine, Department of Cellular Biotechnologies and Hematology, Sapienza University of Rome) were used as a cell model for proliferation study and maintained in RPMI-1640 complete culture media containing 10% FBS, penicillin/streptomycin plus glutamine at 37 °C in 5% CO2. Upon thawing, cells were passaged once prior to amplification for the experiment. Cells were then harvested, counted, and washed twice in serum-free solutions and re-suspended in PBS for further staining.

Cells fluorescent dye labeling

To track cell proliferation by dye dilution establishing the daughter progeny of a completed cell cycle, cells were stained with CellTrace™ Violet stain (CTV, C34557, Life Technologies, Paisley, UK), typically used to monitor multiple cell generations. To determine cell viability, prior to dye staining, the collected cells were counted with the hemocytometer using the dye exclusion test of Trypan Blue solution, an impermeable dye not taken up by viable cells. For the dyes staining, highly viable 20 × 106 cells were incubated in a 2 ml solution of PBS containing CTV (1/1000 dilution according to the manufacturer’s instruction) for 25 min at room temperature (RT) mixing every 10 min to ensure homogeneous cell labeling. Afterward, complete media was added to the cell suspension for an additional 5 min incubation before the final washing in PBS.

Cell sorting

Jurkat cells labeled with dyes were sorted using a FACSAriaIII (Becton Dickinson, BD Biosciences, USA) equipped with Near UV 375 nm, 488 nm, 561 nm, and 633 nm lasers and FACSDiva software (BD Biosciences version 6.1.3). Data were analyzed using FlowJo software (Tree Star, version 9.3.2 and 10.7.1). Briefly, cells were first gated on single cells, by doublets exclusion with morphology parameters, both side and forward scatter, area versus width (A versus W). The unstained sample was used to set the background fluorescence for each channel. For each fluorochrome, a sorting gate was set around the max peak of fluorescence of the dye distribution64. In this way, the collected cells were enriched for the highest fluorescence intensity for the markers used. Following isolation, an aliquot of the sorted cells was analyzed with the same instrument to determine the post-sorting purity and population width, resulting in an enrichment > 99 % for each sample. See Supplementary Figures for more details.

Time course kinetic for dye dilution assessment

The sorted cell population was seeded into a single well of a 6-well plate (BD Falcon) at 1 × 106 cells/well and kept in culture for up to 72 h. To monitor multiple cell division, an aliquot of the cells in culture was analyzed every 18, 24, 36, 48, 60, and 72 h for the fluorescence intensity of CTV dye by the LSRFortessa flow cytometer. To set the time zero of the kinetic, prior culturing, a tiny aliquot of the collected cells was analyzed immediately after sorting at the flow cytometer. The unstained sample was used to set the background fluorescence as described above. Every time that an aliquot of cells was collected for analysis, the same volume of fresh media was replaced in the culture.

Expectation-Maximization and the Gaussian Mixture Model

We used the Expectation-Maximization (EM) algorithm to detect the clusters in Gaussian Mixture Models65. The EM algorithm is composed of two steps the Expectation (E) step and the Maximization (M) step. In the E-step, for each data point f, we used our current guess of πg, μg, and σg, to estimate the posterior probability that each cell belongs to generation g given that its fluorescence intensity measure as f, γg = P(g∣f). In the M-step, we use the fact that the gradient of the log-likelihood of p(fi) for πg, μg, and σg can be computed. Consequently, the expression of the optimal value of πg, μg, and σg is dependent on γg. It is shown that under, certain smoothness conditions the iterative computation of E-stem and M-step leads us to the locally optimal estimate of the parameters πg, μg, and σg, and returns the posterior probability γg which weights how much each point belongs to one of the clusters. Here, we used this model to perform cluster analysis and detect the peaks which correspond to different generations. Then, we estimated πg, E[fg], and Var[fg] from these clusters.

Gillespie simulation

To validate the mathematical model that was formulated, stochastic simulations of the growth and dividing cell population were carried out. Note that, through simulation, we can also know the birth and division sizes and can therefore compare the trends of Δ Vs < sb > .

In particular, simulations were performed starting from N = 1000 initial cells, having initial size randomly sampled from a normal distribution of mean μs and variance \({\sigma }_{s}^{2}\).

For each cell, a division time is extracted from the probability distribution P(td) via inverse transform sampling. For the considered system, P(td) is given by33:

$$P({t}_{d})=1-\exp \left(-\int_{0}^{{t}_{d}}dth(s)\right)$$
(17)

Upon division, each cell is split into two new daughter cells, each inheriting a fraction p and (1 − p) of the mother size, respectively.

Used parameters

Simulation results shown in Fig. 2d, e and Fig. 4b, d, e, f are obtained running Gillespie simulations and/or solving Eq. (14) with the following default parameters κ = 5, λ = 1.6, α = 1, β = 2, Q = 3, < s > 0 = 1, CV0 = 0.15, and \(\pi (f)={{{{{{\mathcal{N}}}}}}}(0.5,0.001)\). Curves of panel (b1) are obtained with all default parameters but < s > 0, that assumed values of 0.8, 0.9, 1.0, and 1.1. Curves of panel (b2) are obtained with all default parameters but λ, which assumed values of 0.8, 1.6, and 3.2. Graphs in panel (d1) are obtained with all default parameters but CV0, which assumed values of 0.15, 0.17, and 0.2. Graphs in panel (d2) are obtained with all default parameters but β, that assumed values of 1, 2, 3, and 4.

Approximate Bayesian Computation Sequential Monte Carlo

Approximate Bayesian Computation Sequential Monte Carlo (ABC SMC) for parameter estimation has been performed via the astroABC python library51. The sampler has been initialized with uniform priors and the following default settings: ’dfunc’:dist_metric, ’adapt_t’: True, ’pert_kernel’:2. The cost function has been defined as the squared root of the sum of the squared residual between experimental and predicted fractions of cells per generations.