Accurate measurements of delayed neutron data for reactor applications: methodology and application to ²³⁵U(n_th,f)

Abstract

Large inconsistencies still exist in nuclear data libraries regarding the kinetic parameters of delayed neutron (DN) precursors. As an example, there is a 17% gap between ENDF-B/VIII.0 and JEFF-3.3 on the average lifetime T_1/2 of DN precursors from thermal fission of ²³⁵U. This parameter is of major importance for reactivity predictions of nuclear reactors in nominal or accidental configurations. In this context, CEA is actively participating to the ALDEN project (Average number and Lifetime of DElayed Neutrons) which aims at providing the nuclear data community with new data sets of DN from thermal and fast neutron induced fission of various actinides. A dedicated experimental setup was designed and optimized for that purpose and is presented in this paper. It consists of a “long counter” detector containing 16 proportional counters filled with ³He, embedded in a high density polyethylene matrix. The detector surrounds a fissile target prepared in the form of a miniature fission chamber, containing a few hundreds of micro-grams of fissile material. This set-up is connected to fast and efficient neutron shutters that can produce step-irradiations of variable durations. The equations driving the DN counting following step-irradiations of the fissile target are established and discussed in the perspective of DN yield or group parameter measurement. A comprehensive analysis of the different steps of data reduction is detailed: dead time characterization, Region of Interest (ROI) determination, absolute and relative efficiency calibration, fission rate estimation, irradiation time and background determination, DN decay curve production and physical parameter fitting. Following a prototype experiment performed in 2018 at the PF1b cold neutron beam line of Institute Laue Langevin (ILL, Grenoble, France), we discuss here the analysis of two campaigns occurring in 2019 and 2021 in which significant improvements were achieved in terms of background minimization, counting statistics and fission rate determination. The achievements of this work are the measurement of the delayed neutron emission per fission for the thermal neutron induced fission of ²³⁵U, estimated at (1.625 ± 0.010) % and the group parameters leading to an estimated lifetime of ${T}_{1/2}$ = (8.87 ± 0.10) s. Those results are consistent with the values recommended by the IAEA/CRP work and they come with reduced uncertainties compared with previously published results.

1 Introduction

After the fission process takes place, most of fission products are naturally unstable. Being neutron-rich isotopes, they undergo a series of β⁻ decays to reach stability. For a fraction of those decays, when the excitation energy Q_β is larger than the neutron separation energy S_n of the daughter nucleus, a (β,n) radioactive decay can occur (or even (β,2 n) if Q_β > S_2n). As this emission results from the radioactive decay of the parent isotope (named «precursor»), it usually happens long after the fission (from milliseconds to several minutes). This is why we denote them «delayed neutrons» (DN).

In the field of reactor physics, the DN emission is described by 3 important sets of data [1]:

• the yield ${\nu }_{d}$, that quantifies the average number of DN emitted per fission,

• the group parameters (${\lambda }_{k},{a}_{k})$, that describe the kinetics of DN emission from group k as a sum of exponential terms ${a}_{k}\text{exp}\left(-{\lambda }_{k}t\right)$ with decay constants ${\lambda }_{k}$ and relative abundance ${a}_{k}$ (${\sum }_{k}{a}_{k}=1)$,

• the group spectra ${\chi }_{d,k}$ that represent the average energy distribution of DN emitted from group $k$.

In a thermal fission reactor, the DN population can be as low as 0.7% of the total neutrons, but still drives the kinetic behavior of the reactor. In a normal or accidental scenario, the prediction of the reactor’s reactivity is strongly dependent on the kinetic parameters of DN precursors. The dynamic behavior of a nuclear reactor relies on the so-called “inhour equation”. This is a derivation from the point kinetic equations, coupling the neutron density to the precursor concentration with time. Under the assumption of a negligible contribution of the source, the dynamic reactivity ρ (in pcm = 10^–5 dk/k) is related to the asymptotic reactor period T = 1/ω as follows:

$$\rho =\Lambda \omega +\sum_{k=1}^{{n}_{prec}}\frac{{\beta }_{eff,k}\omega }{\omega +{\lambda }_{k}}$$

(1)

${\beta }_{eff,k}$ is the effective delayed neutron fraction for the $k$–th DN group, ${\lambda }_{k}$ the decay constant for the $k$–th DN group, $\Lambda$ the mean generation time. The concept of “effectiveness” in the DN group fraction is addressing the ability to cause a fission, which depends on the fissionable nuclide and on the incident neutron energy E. It can be expressed as follows:

$${\beta }_{eff,k}=\frac{\sum_{ i}{\int }_{0}^{\infty }{\phi }^{+}\left({E}{\prime}\right){\chi }_{d,i,k}({E}{\prime})d{E}{\prime}{\int }_{0}^{\infty }{a}_{k,i}\left(E\right)\overline{{\nu }_{d,i}}\left(E\right){\Sigma }_{f,i}\left(E\right)\phi \left(E\right)dE}{\sum_{i}{\int }_{0}^{\infty }{\phi }^{+}\left({E}{\prime}\right){\chi }_{t,i}({E}{\prime})d{E}{\prime}{\int }_{0}^{\infty }\overline{{\nu }_{t,i}}\left(E\right){\Sigma }_{f,i}\left(E\right)\phi \left(E\right)dE}$$

(2)

${\phi }$ and ${\phi }^{+}$ are respectively the forward and adjoint flux, ${\Sigma }_{f}$ the macroscopic fission cross section, $a$ the delayed neutron relative abundance, ${\chi }_{d}$ and ${\chi }_{t}$ respectively the delayed and total (prompt + delayed) neutron spectrum, $\overline{{\nu }_{d}}$ and $\overline{{\nu }_{t}}$ respectively the average number of delayed and total (prompt + delayed) neutrons per fission, i is the index in the list of fissionable nuclides.

While the fission cross section and prompt neutron yield are now well-established nuclear data (uncertainty can go even below ± 0.5%), the delayed neutron yield remains poorly known for the most important actinides. From the recently published report of the Coordinated Research Project of the IAEA [2], the uncertainty on the delayed neutron yield of ²³⁵U is evaluated to be 3% (1σ) from the macroscopic measurement method and up to 5% [3] from the microscopic one. Furthermore, in standard nuclear data libraries, such as JEFF-3.3 [4] or ENDF-B/VIII [5], inconsistencies can be found for the group parameters of ²³⁵U, impacting the calculation of the dynamic reactivity up to 17% [6]. These conclusions strongly support the need for new experimental data of high quality, in order to reduce the uncertainty in DN data.

Another motivation for producing new experimental data is the change from the historical 6-group DN model to a 8-group model, with a consistent set of half-lives, now adopted in the JEFF nuclear data library since 2002. Because most of the experimental decay curves were not preserved, the fitting of the original raw data with the 8-group model cannot be done and what only remains is a set of 4 to 6 group fitted parameters [7]. In the 1990s, the “expansion technique” was suggested by Spriggs and Campbell, in order to expand the original fitted parameters into an 8-group model. However, the authors pointed out the need for new experiments in order to fit the data in 8 groups and to produce a more rigorous uncertainty estimation [8].

In order to address the aforementioned listed issues, a collaboration framework called ALDEN (Average number and Lifetime of DElayed Neutrons) was established among laboratories involved in nuclear data measurement and/or evaluation (CEA/DES, CEA/DRF, CNRS/LPSC, CNRS/L2I, CNRS/LPC Caen, GANIL, ENSICAEN and University of Caen). The objective of this collaboration is to develop optimized experimental set-ups and measurement methods to produce accurate DN yield and group constant data. The project aspires to cover the list of actinides involved in current and future reactor concepts (²³⁵U, ²³⁸U, ²³⁹Pu, ²⁴¹Pu, and others), from the thermal to the fast (E $\upepsilon$ [0–20 MeV]) energy range. In this paper, we present the experimental set-up and method developed for thermal neutron data measurements, and a first application for ²³⁵U thermal fission.

The paper core s composed of four parts. The first one (part 2) presents the theoretical background and literature review of experimental methods for DN measurements. The second one (part 3) describes the key elements of the experimental set-up. The third one (part 4) details the different steps of the data processing and the efficiency calibration of the neutron detector. The last one (part 5) present the experimental results of the data acquired at ILL with the ²³⁵U target.

2 Theoretical background and literature review

2.1 Microscopic versus macroscopic approach

The measurement of DN properties can be performed with two different experimental techniques. One is based on a macroscopic approach, in which we measure the DN total emission following fission, after a burst or a step irradiation. The second one is based on a microscopic approach and consists in measuring the characteristics of individual neutron precursors (half-life, fission yield and DN probability) and applying the summation method [3]. Both approaches have pros and cons that we discuss here.

The macroscopic approach is the historical method, applied since the 1940s, from which the first data were published. It considers the DN emission rate $N(t)$ as a semi-empirical law, containing the DN data of interest. As the DN total emission rate is driven by the sum of hundreds of radioactive decays, the most usual model to represent its kinetics is a sum of n exponential terms characterized by an abundance (noted ${a}_{k}$) and a radioactive decay constant (noted ${\lambda }_{k}$). Assuming that the activity of all DN precursors is saturated, following a long irradiation time, the DN total emission rate per fission $N(t)$ can be written as follows, after the irradiation stop ($t=0)$:

$$N(t)=\overline{{\nu }_{d}}\sum_{k=1}^{n}{a}_{k}{e}^{-{\lambda }_{k}t}$$

(3)

G.R. Keepin performed several tests to evaluate the optimum number of parameters n to fit the data [21]. Six groups, i.e. 12 free parameters of relative abundances ${a}_{k}$ and decay constants ${\lambda }_{k}$ were found to be optimal to minimize the error in the Least Square Fit (LSF) of the experimental data. G.R. Keepin performed a comprehensive work of delayed neutron measurements for thermal fission of ²³³U, ²³⁵U and ²³⁹Pu, and fast fission of ²³³U, ²³⁵U, ²³⁸U, ²³⁹Pu, ²⁴⁰Pu, and ²³²Th. Thanks to the summed contribution of tens to hundreds of DN precursors, the counting statistics is usually very good and precisions of the order of 3–10% can be reached on the determination of ${\nu }_{d}$. Many of the measurements performed by Keepin in the 1960s are still among the most accurate data in the literature. Among the cons of the method, the irradiation of the fissile sample and the subsequent measurement after the irradiation interruption usually implies a fast transfer from its irradiation location to a position far from it, in order to reduce the background. Such transfer usually takes hundreds of milliseconds during which shortest-lived delayed neutron precursors may be lost. As the DN yield is proportional to the DN emission rate after the beam stop, this transfer time may result in an increased uncertainty due to model extrapolation. Indeed, Eq. (3) corresponds to an ideal situation in which the counting of DN starts exactly at the beam stop. If this assumption is not met, typically for a waiting time of hundreds of milliseconds, it is necessary to account for the kinetics behavior of DN emission, which leads to additional uncertainties in the estimation of $\overline{{\nu }_{d}}$. Moreover, the model does not have any predictability on the energy dependence and the DN abundances from different fissionable nucleus are considered independent, while they share the same DN precursors.

During the 1970s, with the much better understanding of the physics of DN, a microscopic approach was introduced to overcome the limitation occurring in the measurement of the shortest-lived DN groups and to extend the calculation of group parameters to other fissionable isotopes. It is also referred as the “summation method”, as the DN yield is the sum of all individual neutron precursors’ contributions, as follows:

$$\overline{{\nu }_{d}}=\sum_{precursor\, k}{P}_{nk}{Y}_{nk}$$

(4)

${P}_{nk}$ is the neutron emission probability of DN precursor $k$ and ${Y}_{nk}$ the cumulative fission yield of precursor $k$. For summation calculations of DN group parameters, a more elaborate equation must be written, taking into account the kinetics of precursor decays and their build-up by β⁻ and/or (β,n) decay of their parent nuclides.

The CRP report [2] presents the most recent summation calculations from the recommended JEFF-3.1.1 library for fission yields and ${P}_{n}$ data from the evaluation work of IAEA. While the computed values are mostly consistent with the ones obtained from the macroscopic approach, the uncertainty is at least twice larger (> 5%), essentially because of the uncertainty on fission yields. Due to this, summation calculations are still far from reaching the target uncertainty required for $\overline{{\nu }_{d}}$ in most reactor calculation studies (typically 1–2%). However, the microscopic approach is a powerful method to add physical constraints in the evaluation of macroscopic quantities such as: number of groups to represent the DN decay, energy dependence with the neutron energy, estimation of DN properties for highly radioactive or rare materials (²³²U, ²⁴²Cm, ^241mAm…). Indeed, assuming that a consistent set of P_n data could be defined to calculate the standard actinides (²³⁵U, ²³⁹Pu, ²³⁸U….), and that calculation codes like FREYA [9], FIFRELIN [10] or GEF [11] could be used to calculate the fission yield of exotic actinides, the microscopic approach is the only way to provide DN properties with a reasonably good precision. The reverse approach could also be applied as a way to constrain the fission models, based on the prediction of fission observables [2, 3]. For instance, the fission yield energy dependence of ²³⁵U could be benchmarked with DN yield measurements for different neutron energies [3], for which the macroscopic approach provides an extensive set of data covering the 0–20 MeV energy range. The step-change of DN yield due to the multiple-chance fission is also a relevant way to constraint nuclear models of several fissionable systems in a simultaneous and consistent way.

2.2 Equation basics

2.2.1 Single irradiation equations

The measurement of DN yield and group parameters by the macroscopic approach is divided in two phases. The first one is the irradiation of the sample, in order to build-up DN precursors. The second one is the measurement of DN emission, when the neutron irradiation and the prompt neutron emission have stopped. Assuming a constant fission rate $F$ during an irradiation time ${t}_{i}$, and the use of a neutron detector with efficiency $\varepsilon (E)$ with the neutron energy $E$, then the counting rate of DN, noted $c(t)$, can be obtained as follows:

$$c\left(t\right)=b\left(t\right)+F\overline{{\nu }_{\text{d}}} \sum_{k=1}^{n}{\varepsilon }_{d,k}{a}_{k}(1-{e}^{-{\lambda }_{k}{t}_{i}}){e}^{-{\lambda }_{k}t}$$

(5)

$b\left(t\right)$ is the background counting rate, ${\varepsilon }_{d,k}$ is the efficiency averaged by the DN group spectra of the k-th group:

$${\varepsilon }_{d,k}=\frac{{\int }_{0}^{\infty }\varepsilon \left(E\right){\chi }_{d,k}\left(E\right)dE}{{\int }_{0}^{\infty }{\chi }_{d,k}\left(E\right)dE}$$

(6)

Equation (5) and (6) contain measured terms ($c(t)$ and$b(t)$), a normalization factor$F$, an efficiency function $\varepsilon (E)$ and 3n + 1 unknown parameters ($\overline{{\nu }_{\text{d}}}$,${\chi }_{d,k}$, ${a}_{k}$ and${\lambda }_{k}$). In this general formulation, all the DN parameters are strongly correlated and cannot be evaluated independently. In order to remove these correlations, it is possible to define measurement conditions in which some terms vanish. To do so, three important conditions must be met:

• ${\varepsilon }_{d,k}$ terms should be energy independent for the different DN group spectra, so that the n terms can be factorized outside of the sum of exponential terms into a single term ${\varepsilon }_{d}$,

• ${t}_{i}$ should be large enough so that ${\lambda }_{k}{t}_{i}$ > > 1,

• $c(t)$ should be measured as close as possible to $t=0.$

Under these assumptions, Eq. (3) is simplified as follows:

$$c\left(t\sim 0\right)=b\left(t\sim 0\right)+F{\nu }_{d}{\varepsilon }_{d}$$

(7)

Then $\overline{{\nu }_{\text{d}}}$ can be determined by measuring the DN instantaneous counting rate at the irradiation stop $c\left(t\sim 0\right)$, without the prior knowledge of (${a}_{k}$, ${\lambda }_{k},$ ${\chi }_{d,k}$) parameters.

Another asymptotic situation could be used to determine ${\nu }_{d}$ based on pulse-type irradiations. In such conditions where ${\lambda }_{k}{t}_{i}\ll 1$, the integration of Eq. 5 over a long counting time ${t}_{c}$ (${\lambda }_{k}{t}_{c}\gg 1$) ends up to:

$${C}_{0}=\underset{\begin{subarray}{c}{t}_{i}\to 0 \\ {t}_{c}\to \infty \end{subarray}}{\text{lim}}{\int }_{0}^{{t}_{c}}c\left(t\right)dt={\int }_{0}^{{t}_{c}}b\left(t\right)dt+F\overline{{\nu }_{\text{d}}} {\varepsilon }_{d}{t}_{i}$$

(8)

This alternative method usually involves higher uncertainties because of the reduction of the irradiation time. Moreover, the method requires a very robust irradiation system to repeat short irradiation cycles, as the precision on $\overline{{\nu }_{\text{d}}}$ is linked to the one on ${t}_{i}$. This is why this method is rarely reported in the literature.

Once ${\nu }_{d}$ has been determined, it is possible to measure the DN counting rate as a function of time, and to fit the DN group parameters according to the following model:

$$c\left(t\right)=b\left(t\right)+F\overline{{\nu }_{\text{d}}} {\varepsilon }_{d}\sum_{k=1}^{n}{a}_{k}(1-{e}^{-{\lambda }_{k}{t}_{i}}){e}^{-{\lambda }_{k}t}$$

(9)

In this equation,${\nu }_{d}$ appears as a normalisation factor, independent of the (${a}_{k}$, ${\lambda }_{k}$) terms. By modulating the DN build-up by short (${t}_{i}\le 5$ s) to long (${t}_{i}\ge 50$ s) irradiation times, one can emphasize some exponential terms and reduce others. The combination of several DN decay measurements helps to reduce the degrees of freedom in the fitting process, and lower correlations between group parameters.

Similarly to the Eq. (8), an asymptotic situation can be defined in which we define an almost infinite irradiation time (${t}_{i}\to \infty )$. In such situation, the integral of the counting rate is written as:

$$\begin{aligned}{C}_{\infty }&=\underset{{t}_{i}\to \mathit{\infty }; {t}_{c}\to \infty }{\text{lim}}{\int }_{0}^{{t}_{c}}c\left(t\right)dt\\ &={\int }_{0}^{{t}_{c}}b\left(t\right)dt+F\overline{{\nu }_{\text{d}}} {\varepsilon }_{d}\sum_{k=1}^{n}\frac{{a}_{k}}{{\lambda }_{k}}\end{aligned}$$

(10)

2.2.2 Periodic irradiation equations

The previous equations are related to a single irradiation phase followed by a single cooling phase. In practice, irradiation / cooling phases are repeated several times in order to improve the counting statistics and to approach DN saturation by a repetition of long irradiation time versus cooling time (typically in a ratio > 10).

Indeed, let’s consider a repetition of $p$ cycles composed of beam on (irradiation) / beam off (cooling) phases of respective durations ${t}_{on}$ and ${t}_{off}$. By summing Eq. (5) over the p cycles, the counting rate in the cooling phase becomes:

$$\begin{aligned}c\left(t\right)&=b\left(t\right)+F\overline{{\nu }_{\text{d}}} \sum_{j=0}^{p}\sum_{k=1}^{n}{\varepsilon }_{d,k}{a}_{k}(1-{e}^{-{\lambda }_{k}{t}_{on}})\\ &\qquad\quad {e}^{-{\lambda }_{k}\left[(j-1)\left({t}_{on}+{t}_{off}\right)+t\right]}\end{aligned}$$

(11)

Considering the asymptotic behavior when $p\to \infty$, we end up with the following equation:

$$c\left(t\right)=b\left(t\right)+F\overline{{\nu }_{\text{d}}} \sum_{k=1}^{n}\frac{1-{e}^{-{\lambda }_{k}{t}_{on}}}{1-{e}^{-{\lambda }_{k}({t}_{on}+{t}_{off})}}{\varepsilon }_{d,k}{a}_{k}{e}^{-{\lambda }_{k}t}$$

(12)

We understand from this equation that if $\frac{{t}_{off}}{{t}_{on}}\ll 1,$ the ratio term of Eq. (12) tends to unity. Let’s consider a typical cycle of 5 s irradiation followed by 0.5 s cooling: such cycle provides a saturation rate of 92% on the longest-lived DN group, which considering a single irradiation, would need 200 s. We understand that for a fixed time of measurement, it is possible to record much more statistics in such short irradiation cycles than using long irradiations. The only drawback of the approach is that it is required to discard a transient period of 5 to 10 min before the asymptotic behavior of Eq. (13) can be verified.

2.2.3 Averaging equations

Once the saturation regime is reached, repeated cycles can be considered equivalent and we may sum them in order to increase the counting statistics. Let ${c}_{i}\left(t\right)$ be the counting rate of DN of the i-th cycle over a total of ${n}_{c}$ cycles. If the neutron flux remains stable during the cycle irradiations, then the distribution of ${\left[{c}_{i}\left(t\right)\right]}_{i=1..{n}_{c}}$ can be considered as a random sample of the random variable $c$, with the mean noted $\overline{c }$ and the variance of the mean noted $var(\overline{c })$ calculated as follows:

$$\overline{c }\left(t\right)=\frac{1}{{n}_{c}}\sum_{i=1}^{{n}_{c}}{c}_{i}(t)$$

(13)

$$var(\overline{c }\left(t\right))=\frac{1}{{n}_{c}}\sum_{i=1}^{{n}_{c}}\frac{({c}_{i}\left(t\right)-\overline{c }\left(t\right))^{2}}{{n}_{c}-1}$$

(14)

2.3 Fission rate determination

One of the dominant uncertainty in the measurement of the DN yield comes from the fission rate $F$. We present below four different methods that can be used to measure it.

2.3.1 Activation foil method

The most common method for determining the sample fission rate relies on its definition:

$$F={n}_{i}\int {\sigma }_{f}\left(E\right)\phi \left(E\right)dE$$

(15)

where ${n}_{i}$ is the number of atoms of the fissile isotope, ${\sigma }_{f}\left(E\right)$ the microscopic fission cross section, $\phi \left(E\right)$ the neutron flux.

In this equation, ${n}_{i}$ is assumed to be known from the manufacturing process of the sample, ${\sigma }_{f}\left(E\right)$ is an input quantity taken for instance from the JEFF-3.3 library and the only unknown term is the neutron flux. The latter can be determined by using an activation foil, irradiated at the same place as the fissile sample. From the saturated activity of this foil, it is possible to determine $F$ as follows:

$$F=\frac{{n}_{i}{\int }{\sigma }_{f}\left(E\right)\phi \left(E\right)dE}{{n}_{f}{\int }\sigma \left(E\right)\phi \left(E\right)dE}{A}_{sat}$$

(16)

where ${n}_{f}$ is the number of atoms of the activation foil, $\sigma \left(E\right)$ the microscopic activation cross section, ${A}_{sat}$ the saturated activity of the activation foil, defined as:

$${A}_{sat}=\frac{\lambda {N}_{\gamma }{t}_{m}}{{\eta }_{\gamma }{I}_{\gamma }{t}_{a}(1-\text{exp}\left(-\lambda {t}_{m}\right))\text{exp}\left(-\lambda {t}_{c}\right)(1-\text{exp}\left(-\lambda {t}_{i}\right))}$$

(17)

where $\lambda$ is the decay constant of the activated nuclide, ${I}_{\gamma }$ the intensity of the measured γ-ray, ${\eta }_{\gamma }$ its photopeak efficiency, ${t}_{m}$ the actual measurement time, ${t}_{a}$ the active (dead-time corrected) measurement time, ${t}_{c}$ the cooling time from the end of the irradiation to the start of the measurement, ${t}_{i}$ the irradiation time.

The integral terms in Eq. (16) can be determined thanks to a Monte-Carlo model of the experimental set-up, in order to account for the actual shape of the neutron flux.

2.3.2 Active target signal method

If the fissile sample can be prepared in the form of a thin disk and put in a fission chamber (FC), the fission rate $F$ can be determined through the recording of the signal resulting from the charge collected in the slowing down of one or two fission fragments within the gas of the FC:

$$F=\varepsilon S$$

(18)

where $\varepsilon$ is the intrinsic efficiency of the FC, defined as the counting rate over the fission rate. This parameter depends strongly on the thickness of the fissile deposit, as well as the deposit geometry and the gas pressure. As this parameter cannot be easily estimated through simulation, it is usually determined using calibrated neutron fields, such like thermal columns or pure fission spectrum [22]. As these fields are usually calibrated using activation foils, this method is no more than a derivation of the previous one.

2.3.3 Post-irradiation spectroscopy method

The most usual method for fission rate determination is the spectroscopy of gamma rays emitted from fission products. The method has the advantage to obtain the fission rate, without the prior knowledge of the mass of fissile isotope. It is determined through the saturated activity of one of the fission products, divided by its cumulated fission yield ${Y}_{c}$ [23]:

$$F=\frac{{A}_{sat}}{{Y}_{c}}=\frac{\lambda {N}_{\gamma }{t}_{m}}{{Y}_{c}{\eta }_{\gamma }{I}_{\gamma }{t}_{a}(1-\text{exp}\left(-\lambda {t}_{m}\right))\text{exp}\left(-\lambda {t}_{c}\right)(1-\text{exp}\left(-\lambda {t}_{i}\right))}$$

(19)

Note that the method applies preferentially to fission products for which the parent nuclide has a significantly shorter half-life compared to the measured radionuclide, so that its decay can be approximated by a single exponential term. The most common fission products that meet these requirements are: ⁹²Sr, ¹⁰³Ru, ¹³¹I, ¹⁴⁰La. The latter are selected because of their well-known decay schemes, the most intense gamma rays having uncertainties of 1% or less on their emission probability.

In the case of large fissile samples, the determination of the photopeak efficiency ${\eta }_{\gamma }$ may require self-attenuation and solid angle corrections (also referred as “efficiency transfer corrections”). They can be obtained through a Monte-Carlo model of the set-up [24].

2.3.4 Neutron emission rate method

An alternative rarely used method for fission rate determination is the counting of total (prompt + delayed) neutron emission during the irradiation of the target [25]. In this case, the DN yield is actually estimated relatively to the prompt neutron yield. Similarly to the DN Eq. (12) in cycle irradiations, the counting rate measurement of prompt + delayed neutrons is written as:

$$c\left(t\right)=b\left(t\right)+\overline{{\nu }_{\text{p}}} {\varepsilon }_{p}F+\overline{{\nu }_{\text{d}}} F\sum_{k}{a}_{k}{\varepsilon }_{d,k}\left[\left(1-{e}^{-{\lambda }_{k}t}\right)+\sum_{j=0}^{p}\left(1-{e}^{-{\lambda }_{k}{t}_{on}}\right){e}^{-{\lambda }_{k}(t+{t}_{off}+j{(t}_{on}+{t}_{off})}\right]$$

(20)

${\varepsilon }_{p}$ is the efficiency for prompt neutron detection, ${t}_{on}$ and ${t}_{off}$ are respectively the irradiation and cooling times.

Then the fission rate is obtained by the integral of this equation over the irradiation time ${t}_{on}$:

$$F=\frac{{c}_{on}-{b}_{on}}{\begin{array}{c}\overline{{\nu }_{\text{p}}} {\varepsilon }_{p}+\overline{{\nu }_{\text{d}}} \sum_{k}{a}_{k}{\varepsilon }_{d,k} \\ \left[1-\frac{1-{e}^{-{\lambda }_{k}{t}_{on}}}{{\lambda }_{k}{t}_{on}} \frac{1-{e}^{-{\lambda }_{k}{t}_{off}}}{1-{e}^{-{\lambda }_{k}{{(t}_{on}+t}_{off})}} {e}^{-{\lambda }_{k}{(t}_{off}+{t}_{on})})\right]\end{array}}$$

(21)

${c}_{on}$ and ${b}_{on}$ are respectively the average counting rate of the fissile target and of the counting rate due to the background.

In a steady-state situation where the DN precursors are close to saturation, the term in brackets tends to unity and the fission rate equation can be simplified into:

$$F=\frac{{c}_{on}-{b}_{on}}{{\epsilon }_{p}\overline{{\nu }_{\text{p}}} +{\epsilon }_{d}\overline{{\nu }_{\text{d}}}}$$

(22)

By applying Eq. (22) in Eq. (7), we obtain:

$$c\left(t=0\right)={b}_{off}+({c}_{on}-{b}_{on})\frac{{\varepsilon }_{d}\overline{{\nu }_{\text{d}}} }{{\epsilon }_{p}\overline{{\nu }_{\text{p}}} +{\epsilon }_{d}\overline{{\nu }_{\text{d}}}}$$

(23)

${b}_{off}$ is the background counting rate in the “beam off” situation.

The advantage of the method lies in the fact that it makes use of a ratio of efficiencies between delayed and prompt spectrum. Indeed, many sources of systematic errors in the determination of the detection efficiency may vanish when considering relative values instead of absolute ones. However, the precision of the method is related to the maximization of ${c}_{on}$ against ${b}_{on}$. In thermal neutron irradiation experiments, the use of neutron filter materials like boron or cadmium can reduce drastically ${b}_{on}$, while having minor impact on the measurement of delayed and prompt neutrons with mean energies of respectively 500 keV and 2 MeV. This is the strategy adopted in the set-up we will detail in Sect. 3.

2.4 Efficiency determination

The determination of $\overline{{\nu }_{\text{d}}}$ from Eqs. (7) and (23) requires the knowledge of the absolute efficiency for prompt and delayed neutron counting. As it is not possible to use calibrated neutron sources with the same spectrum, the usual method is to build a Monte-Carlo model of the neutron detector and to validate it with appropriate experiments.

One method can use calibrated neutron sources of radioactive materials [26]. This can be done for instance with Am-Li sources of mean energy of 470 keV, close to the one of delayed neutrons and with ²⁵²Cf sources of mean energy 2.1 MeV, close to the one of prompt neutrons. These sources are usually small, with a low anisotropy factor, and are characterized in emission rate with low uncertainties (typically 1% or less), making them very appropriate for this application. However, they provide integrated values of the efficiency over wide energy regions due to the shape of the source neutron spectrum.

It is also possible to use calibrated neutron fields from accelerators [26]. These facilities can produce neutrons from accelerated charged particle beams (protons, deutons, tritons…) sent to a target (deuterium, tritium, lithium, scandium…). Depending on the reaction type and energy of the charged particles, the neutron fields can be highly anisotropic, and have usually a strong energy / angle dependence. The neutron flux is usually calibrated at (1 m, 0°) with an uncertainty of about 3%. The advantage of using accelerators instead of neutron sources lies in the possibility of having quasi mono-energetic beams, as well as in the flexibility of accessible energies (from a few keV to 20 MeV).

3 Description of the experimental set-up

3.1 The PF1B instrument of ILL

Our experiment takes place at the PF1B instrument of the Institute Laue Langevin (ILL). This is a versatile facility used for particle and nuclear physics experiments. It delivers cold neutron beams (E_n = 5 meV), in variable shapes and polarized states, with a flux up to 2.10¹⁰ n.cm⁻².s⁻¹. It is composed of a casemate area where the neutron beam characteristics are adjusted, and an experimental zone downstream of it where the set-up is installed. The beam characteristics are described in more details in [28].

3.2 The LOENIEv2 “long counter”

Our detector for DN measurement is an upgrade of a previously designed long counter for P_n (neutron probability) measurement at ILL [29]. This new version, called LOENIEv2, is composed of sixteen proportional counters (PCs) filled with 10 bars of ³He, placed in a cylindrical high density polyethylene (HDPE) matrix, covered by a 10 mm layer of boron rubber. The HDPE matrix has a central hole, covered with 7 mm boron rubber, at the center of which the fissile target is installed for irradiation. Sectional views of the detector are presented in Fig. 1.

Fig. 1

Radial (left-side) and axial (right side) sectional views of the LOENIEv2

An optimization of the number and position of PCs inside the HDPE was performed thanks to TRIPOLI-4® Monte-Carlo calculations, in order for the sum of their individual efficiencies to reach a constant behavior versus energy for a wide neutron energy range. Based on the simulation results, PCs are arranged in three rings: one close to the center at 5.3 cm (4 detectors represented in green), one at 15 cm (8 detectors represented in blue) and the last one at 16 cm (4 detectors represented in red). In the neutron energy range of interest [0.1–1 MeV], the absolute efficiency for the sum of the sixteen PCs is close to 20% and the relative variation is 2%. This is obtained thanks to a balance of efficiencies between the inner ring, with a maximum value for 10–100 keV neutrons, and the outer rings, with a maximum value for 3–4 MeV neutrons (see Fig. 2). A π/4 rotation symmetry between the different PC is of interest for reproducibility verifications and as a way to minimize positioning errors of the fissile target in the central channel.

Fig. 2

Efficiency of the LOENIEv2 based on TRIPOLI-4.® calculations (in blue: sum of the 16 tubes; in red sum of 4 inner tubes; in violet: sum of the 8 intermediate tubes; in yellow: sum of the 4 outer tubes)

The system is mounted at the exit of the beam line and surrounded by concrete blocks for biological protections (see Fig. 3).

Fig. 3

LOENIEv2 long counter, during the assembling of the HDPE matrix (left-side) and final installation in the PF1B experimental area (right side)

3.3 Fissile target

The fissile target is a miniature fission chamber (MFC) manufactured by CEA (CFP12 type). It is composed of a Ti backing disk, on which the fissile material is electro-deposited, forming a spot of 8 mm in diameter. The latter is embedded into a Ti body of 12 mm outer diameter. A miniature coaxial connector of 4 mm in diameter made it possible to plug the detector onto a coaxial cable (see Fig. 4).

Fig. 4

Photos of the MFC (left-side) and the airtight tubing (right side) in which it is enclosed

The ²³⁵U mass in the fissile deposit was chosen so that the maximum counting rate in a PC (due to prompt + delayed neutrons) does not reach more than 2.10⁴ c/s, in order to minimize the dead time corrections. Gamma spectroscopy of the MFC was performed in the MADERE facility of CEA [30], prior to irradiation, to measure the activity of the 185.7 keV gamma-ray from ²³⁵U decay and thus control the mass of the actinide. An activity of 16.34(25) Bq was obtained, which corresponds to 204.3(30) µg of ²³⁵U.

The MFC is placed under low pressure in a closed airtight tubing system of 1 mm in thickness, which acts as a safety barrier, monitored by a pressure gauge. It is made of an aluminum pipe and tore joint links which allows connecting the elements (pump and pressure gauge). The signal transmission cable from the fission chamber is connected to an airtight BNC feedthrough (see Fig. 4).

3.4 Neutron shutter systems

The shutter system is an important device for accurate DN measurements. It has to be fast enough to cut the incoming neutron beam in a few milliseconds and efficient enough to reduce the background as low as possible compared to the DN counting. Two systems were developed to meet these two requirements.

The first one is a turning brushless motor supporting an aluminum plate on which 2 neutron absorbers are placed (see Fig. 5). When correctly aligned and parallel to the neutron beam, neutrons fly through the gap between the screens. By means of a rotation of 90°, the screens go perpendicular to the beam and capture thermal neutrons. The size, the thickness, and the absorbing materials were chosen in such a way to reduce the fission rate in the target by a factor of 10⁸. The screens were made of a 2 mm-layer of B₄C followed by 1 mm-layer of Cd. The two absorbing layers were designed to minimize the energetic gamma rays that would be produced in the case of using only Cd for the beam shutter. At the same time, they guarantee a better absorption than a screen entirely made of B₄C. A video-recording of the shutter rotating is used to estimate the rotation time from an angle where the beam is fully absorbed to an angle where it is fully opened: it was measured to be approximatively 4 ms.

Fig. 5

Picture of the two neutron shutters placed inside the PF1B casemate

The very high efficiency for thermal neutron absorption in the fast shutter has a counterpart: the high ¹⁰B(n,α)⁷Li reaction rate in the B₄C plates produce parasitic reactions of ¹⁰B(α,n)¹³N and ¹¹B(α,n)¹⁴N. They result in a fast neutron source that can travel up to the LOENIEv2 long counter, located about 2 m after the fast shutter, and are indistinguishable from the DN neutrons from the target. This is why a second system was placed after the first one, in order to minimize the contribution of this fast neutron source. It consists of a square block of 10 × 10x10cm of borated polyethylene (BPE), mounted on a vertical piston. When the beam is on, the system is shifted 5 cm below the beam centre. As soon as the fast shutter is controlled to interrupt the beam, the second shutter is activated. The translation over the 10 cm of vertical amplitude takes about 100 ms. As this transient time is quite long compared to the one of the fast shutter, this second system was only used for DN counting over long periods, typically up to 500 s after the irradiation interruption, where the measurement of the longest-lived DN groups rely on the minimization of the neutron background.

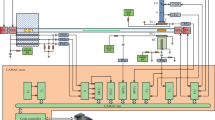
3.5 Data acquisition system

A diagram of the data acquisition system is presented in Fig. 6.

Fig. 6

Diagram of the Data Acquisition System

The ³He PCs were plugged to charge sensitive preamplifiers (CSPA) which shape the short current pulses delivered by the detectors into integrated and exponentially tailed voltage pulses. The latter were fed to two synchronized digitizer cards (CAEN V1724), running a real time digital pulse processing embedded program to process the data flow, detect events and record their arrival time and energy (i.e. the amplitude of the pulses). Raw data buffers were stored into binary files in “list mode” for further data processing. In the case an event was fully processed by the Digitial Pulse Processing (DPP) algorithm, then the energy and time could be assigned non-zero values on the data file. On the contrary, when an event could be identified as flawed or incorrectly processed (due to pile up or any error in the algorithm), its energy was set to zero by convention.

Given the large counting rate delivered by the MFC under irradiation, it was not possible to process the corresponding signal like the others. This is the reason why an analog amplifying stage based on a Canberra ADS7820 as broadband amplifier-discriminator was used. It shaped the current pulses and issued 0–5 V 100 ns TTL pulses thanks to its discriminator stage. The TLL signal was then fed to a scaler module (MDPA Ioxos 1210) which processes the signal to calculate the number of counts per time interval (with a maximum 2¹⁶ time bins).

A third digitizer card (CAEN V1751) was used to record signals from the two shutters. A photodiode was installed in the casemate, perpendicularly to the neutron beam. Its signal was sent to a channel of the V1751 card to provide the time stamp related to the “beam off” situations. For the slow shutter, limit switches were used to record the time stamps of the two situations, with the BPE block at the lowest and highest positions.

All acquisitions schemes were synchronized and the time trigger is issued by a CAEN V1818 controler card and then shared to the CAEN digitizers. In parallel, the beam shutter monitoring and control system was handled thanks to a driver developed by ILL and installed within the monitoring software NOMAD [31]. It is an ILL-developed multi-purpose tool that can handle setting up acquisition modules, collect data and transfer it to a remote storage server. Conveniently, it has also powerful capabilities of sequencing commands in acquisition loops thanks to user-defined scripts.

4 Data processing and efficiency calibration

4.1 Data processing

The overall detection rate issued by the sixteen PCs is the main physical quantity of interest taken as observable in the analytical models. A cycle of irradiations is split into numerous short irradiation runs. Basically, the data reduction consists in processing the numerous raw signals in a consistent manner so as to produce a time series proportional to the target’s neutron detection rate.

Thanks to the symmetries of the LOENIEv2 detection system (four symmetrical quadrants of 4 sub-detectors), it is possible to analyze the signals of each quadrant independently. This allows assessing the quality of the measurement by calculating a dispersion among the four quadrants and, possibly, to exclude outlier values.

The data reduction includes the following steps:

• 1. Conversion of the binary files into a (n × 3) matrix (events stored in raws, time stamp, energy and channel number in columns), thanks to a C +  + dedicated tool;

• 2. Synchronization of time stamps of each run using either the photodiode signal (if exists) or a statistical method based on a counting rate threshold critera: the closure of the beam is taken as the reference time (t = 0);

• 3. Energy rescaling and selection of the neutron events to be processed, by applying a region of Interest (ROI) in the energy range;

• 4. Calculation of the neutron detection rates versus time (by taking the histograms of the events arrival times) of each channel and for each run;

• 5. Correction for counts loss (pile-up and dead time) using an analytical non-extendable dead time model of each channel and for each run;

• 6. Calculation of total and quadrant detection rates for each run;

• 7. Calculation of means and standard deviations of the detection rates over all runs

The final decay curves are fed to the CONRAD nuclear data evaluation tool [33] (version 02_02_2022) to estimate the delayed neutron physical quantities expressed as parameters in the models: DN yield and group abundances. Ad hoc MATLAB functions were built for converting the reduced experimental data into CONRAD input files. We now present a short description for each of these steps.

Step 1: data conversion

First, the binary files recorded by NOMAD are processed by the ALPROC tool (v16), developed in C +  + , based on low levels function libraries provided by ILL. ALPROC collects the unsorted detection events (channel, time stamp, energy), and then stores them into an ASCII file in chronological order. If needed, it also applies a time stamp correction to events which were stored with an incorrect time stamp (in case of data loss for instance). Second, a Matlab routine uploads the ASCII file and stores the raw events into a data structure.

Step 2: time synchronizing

During a measurement, the events are timestamped by the acquisition card itself, the clock of which is not synchronized with the one of NOMAD. In the data file, the reference time (t = 0) is the beginning of the measurement itself, and there is no simple way to synchronize two consecutive measurements.

Since it would be unpractical to record an entire experiment in one datafile (its size would be tens of GB), the choice is made to start a new run of measurement for each sequence of irradiation and stop it at the end of the counting period. This is the reason why a key point in the data processing is to correct the timestamps, meaning to have a reference time synchronized to the beam shutter’s motion. In the first ILL experimental campaign, the synchronization was performed by detecting the edge of the PC counting rate drop, which takes a few milliseconds to be reduced by a factor 10³. For the second and third ILL campaign, a photodiode signal is recorded to have a more precise evaluation of the beam cutting. The time stamp of this signal is used to synchronize the different cycles to a common time reference (t = 0).

Step 3: selecting events of interest

It is known that the 16 detectors do not have exactly the same response in energy. A procedure is applied for rescaling the energy distribution of each detector, so that the neutron peak energy (around 550 LSB) is the same for all detectors (E = 764 keV).

The signal to noise ratio (SNR) is highly dependent on the acquisition parameters, especially the trigger threshold (TT). Ideally, the SNR would be independent on the detector. This would ensure that the region of interest used to discard background noise from neutrons does not change the efficiency between detectors. Practically, it is possible to set the TT parameters so that the background noise is visible but low enough on all channels (see discussion on Sect. 4.2).

Step 4: neutron detection rates time series

After the cut in energy, time series are generated to produce a histogram of arrival times for each detector. For DN yield experiments, the bin width is set constant at 1 ms. For long cycles, the bin width is progressively adapted to follow the DN decay.

Step 5: correction of count losses

An analytical dead time correction is applied on each time series. A so-called non-extendable model is chosen, associated to a dead time parameter τ = 7.6 µs (cf. more details in Sect. 4.3).

Note that the correction factor applied to the counting rate has a significant effect on the counting of prompt neutrons during the irradiation phase and practically no effect on the counting of DN during the decay phase.

Step 6 and 7: group average and generation of CONRAD input files

The physical observable to be fitted by CONRAD is the summed counting rate over the 16 PCs, as a function of time. It is produced by averaging equivalent individual time series. Indeed, when starting a series of beam on / beam off cycles, a transient period appears in which the DN precursors are progressively reaching an asymptotic behavior before all the cycles can be considered “equivalent” (i.e. referring to the same theoretical model). Depending on the cycle characteristics, this transient period can take up to 10 min. As we usually repeat cycles over periods of few hours, we usually discard these first minutes in order to account only for cycles in quasi steady-state behavior.

The uncertainties given to CONRAD correspond to the experimental standard deviation of the mean, assuming that the distribution of counting rates are independent.

4.2 Calibration of PC and settings

It is convenient to consider the long counter as a single detector, the signal of which is simply the sum of the sixteen signals from the PCs. The efficiency of the system could then be obtained by simulations in which the ³He capture rates in the PCs are calculated and summed. The validity of the method relies on two assumptions:

• The detectors should be identical (i.e. same technological parameters like the gas volume and pressure) and thus react the same way to neutrons and gamma rays.

• The signals recorded by the acquisition system should actually give access to the ³He capture rate.

These assumptions were carefully assessed by analyzing the signals of the PCs at several neutron flux levels and for different configurations. They were alternatively loaded in the same hole of the HDPE, with an AmBe source placed in the center of the long counter (Fig. 7).

Fig. 7

Efficiency measurements of each ³He tube, alternatively loaded in the same hole of the HDPE

The spread of individual efficiencies was shown to be less than 1.5%, confirming that the PC can be considered equivalent. The small differences in the detection sensitivity may be attributed to small variations in the gas pressure.

Then, the analysis of the Pulse Height distribution (PHA) exhibits very similar behaviors, whatever the PC and whatever its location in the LOENIEv2 (Fig. 8). The ROI is determined at low flux to be from 10³ LSB to 3.10⁴ LSB. The lower bound was chosen so that it does not cut the neutron distribution, even with high count rates. The upper energy bound allows cutting higher energy parasitic events due to spurious detection in the baseline.

Fig. 8

Energy distribution (pulse height spectrum) of the sixteen PCs. Some background due to gamma rays is visible at the left of the dotted line. A second peak due to neutron interactions is due to pile up

A careful analysis of the Trigger Threshold (TT) setting and its impact on the spectrum shape was also conducted. If it is set to low (TT < 400 LSB), the digitalizer triggers in the baseline, resulting in degrading the signal to noise ratio at low energy (see Fig. 9). If it is set too high (> 600 LSB), the spectrum associated to ³He + n interaction is truncated, resulting in loss of counts that can reach up to 10%. Optimum values were adopted for each PC, ranging from 450 to 550 LSB.

Fig. 9

Impact of the TT on the energy spectrum of one PC of the inner ring

4.3 Dead time correction model

A dedicated experimental campaign was undertaken at LPSC Grenoble to study the dead-time effect in ³He PCs. The experiment uses the 14 MeV neutron source provided by the GENEPI-2 accelerator of the GENESIS neutron facility, through Deuterium/Tritium (D/T) reaction [38]. Two independent methods were applied to estimate the dead-time based on the modulation of the neutron source intensity.

4.3.1 Si-detector method

A silicon detector is mounted 60 cm below the Tritium target, for fusion reaction monitoring, based on the detection of alpha or proton particles (Fig. 10).

Fig. 10

Schematic of the Si detector mounted in the GENEPI-2 accelerator

Such detector has a low sensitivity, resulting in a maximum counting rate of 4.10³ c/s with a dead-time window of the order of 100 ns. The counting loss due to dead-time is negligible over the range of available beam intensities. By correlating the counting rate of this silicon detector for beam intensity No. i, noted ${S}_{i}$, to the one of ³He PC of LOENIEv2, noted ${N}_{i}$, it is possible to estimate a model for dead-time correction according to the following relationship:

$${N}_{i}={N}_{1}\frac{{S}_{i}}{{S}_{1}}$$

(24)

In the following, ${N}_{i}$ is called “rescaled counting rate”.

Our LOENIEv2 long counter was installed about 5 m from the accelerator, in order to cover a range of observed counting rates from 0 to 5.10⁴ c/s. Four PCs, with different efficiencies, were tested independently. 42 different neutron flux values from 0 to 100% were considered and the PC counting rate was measured for each of them. Two models for dead-time correction were tested:

• a non-extendable model with the measured counting rate $M$ being related to the real one $N$ as:

  $$M=\frac{N}{1+\tau N}$$

  (25)

• an extendable model with the measured counting rate $M$ being related to the real one $N$ as:

  $$M=Nexp(-\tau N)$$

  (26)

  Then, introducing Eq. (24) in Eqs. (25) and  (26), we end up with:

• non-extendable model:

  $${S}_{i}=\frac{{M}_{i}}{1-\tau {M}_{i}}\frac{{S}_{1}(1-\tau {M}_{1})}{{M}_{1}}$$

  (27)

• extendable model:

  $${S}_{i}={S}_{1}\frac{1-\tau {M}_{1}}{{M}_{1}}{M}_{1}\text{exp}(\tau {M}_{i})$$

  (28)

  ${S}_{i}$ and ${M}_{i}$ are experimental observables while $\tau$ is the unknown parameter. Applying these models to the data acquired at GENESIS, we obtain the following estimations (see Table 1).

Table 1 Dead-time estimation (in µs) for extendable and non-extendable models over the range [0–2.5 10⁴ c/s] of observed counting rate

We illustrate the agreement between the corrected counting rate and the estimated rescaled counting rate based on the Si detector (see Fig. 11).

Fig. 11

Corrected counting rate against rescaled counting rate for the extendable and non-extendable models (fast neutrons from the D/T reaction of GENESIS)

We observe that none of the two models can correct counting losses due to dead-time over the full range of measured counting rate. As our applications in ILL are limited to a maximum counting rate of 2 10⁴ c/s, we have considered a maximum value of 2.5 10⁴ c/s for the fitting of the $\tau$ parameter in both models. Both models produce similar corrections on the [0–2.5 10⁴ c/s] counting range, without deviations from experimental uncertainties. However, for higher counting rate, the non-extendable models works slightly better and remains consistent within 2σ with the reference curve up to 4 10⁴ c/s. Moreover, values from Table 1 present consistent results from the four selected PCs, confirming that the same value can be attributed to all the PCs. Moreover, the 7.71 ± 0.25 µs value for the non-extendable model is consistent with the first estimate 7.48 ± 0.17 µs obtained from a pulser method, as published in [3].

4.3.2 Ring ratio method

A second method is tested, considering the ratio between the most and least efficient counting tubes, denoted as the ring ratio (noted RR) method. As the counting loss fraction due to dead-time is almost linear with the counting rate, then

Noting ${M}_{l}$ and ${M}_{h}$ the lowest and highest counting the RR decreases almost linearly with respect to the observed counting rate.rates among the 16 PCs and applying a non-extendable model for dead-time correction with a constant value $\tau$ for all the PCs, we can express the observed RR (noted $R$) as a function of the true RR (noted ${R}_{0})$:

$$R=\frac{{M}_{h}}{{M}_{l}}\approx {R}_{0}+\tau {M}_{h}\left(1-\frac{1}{{R}_{0}}\right)$$

(29)

Fitting the experimental observable $R$ as a function of ${M}_{h}$ (here it is for PC No. 16), it is possible to determine the unknown parameters ${R}_{0}$ and $\tau$. Results are given in Table 2.

Table 2 Dead-time and true RR values, resulting from the fitting of experimental data

Similarly to the previous method, it was not possible to fit the RR data on the full counting range. Indeed, the model does not properly correct the counting loss after 3 10⁴ c/s. As a consequence, it was decided to limit the fitting range up to 2.5 10⁴ c/s. The $\tau$ value fitted from this method is consistent with the one of the Si detector method, with a much lower uncertainty. This value was kept as the reference dead-time estimation hereafter.

4.4 Efficiency calibration & validation of Monte Carlo simulations with TRIPOLI-4

4.4.1 NPL calibration measurements

The use of calibrated neutron sources is a suitable method for determining the detector efficiency. Performing the calibration campaign in NPL [39] was motivated by the availability of low energy neutron sources like AmLi, with an average energy similar to the one of delayed neutrons (~ 500 keV). A diversity of higher energy sources allowed coverage of a range from 1.3 to 4.2 MeV as well. Several AmBe sources with different emission rates were used to test the robustness of the dead-time correction. We summarize in Table 3 the characteristics of the neutron sources used for the NPL campaign.

Table 3 Neutron source characteristics

Anisotropy measurements from 0 to 180° were determined by NPL for each source, due to the neutron attenuation in the source material and source container.

Neutron sources were placed at the center of LOENIEv2 for the calibration of the detector efficiency (see Fig. 12).

Fig. 12

Positioning of neutron sources inside the LOENIEv2 detector for efficiency calibration

The absolute efficiency for the source of mean energy E was derived from the following equation:

$$\varepsilon \left(E\right)=\frac{\sum_{k=1}^{16}{c}_{k}\left(E\right)/(1-\tau {c}_{k}\left(E\right))}{N\left(E\right)}$$

(30)

where ${c}_{k}\left(E\right)$ denotes the observed counting rate for the PC No. k, $N\left(E\right)$ the source total emission rate at the time of the experiment, $\tau$ the dead-time parameter adopted in Sect. 4.3.2.

Experimental uncertainties on the determination of the efficiency accounts for:

-Statistics uncertainty due to counting (<0.2%),

-Source emission rate (0.4-0.9%),

-Positioning errors (±2mm axially and ±5mm radially)

The experimental efficiency values are reported in Table 4. They confirm the small variation of efficiency between the AmLi and AmF sources (less than 2%), as expected from the design calculations. The consistency of the results between the 3 AmBe sources (less than 0.4%), with intensities ranging from 1 to 30, is excellent and confirms once again the relevance of the dead-time correction model.

Table 4 Results of efficiency measurements

4.4.2 Validation of the Monte-Carlo model of the LOENIEv2

A Monte-Carlo model of the LOENIEv2 was developed, using the TRIPOLI-4® calculation code [42] using the JEFF-3.3 nuclear data library [44]. The geometry was built based on the mechanical drawings of the HPDE block and datasheets of the ³He tubes from the LNE manufacturer (Fig. 13). The atomic density of ³He was obtained from the ideal gas law. Knowing that the tubes are filled with 3% CO₂, and assuming $T$ = 294 K, we ended up with the following atomic densities:

• ³He: 2.421 × 10²⁰ at/cm.³

• CO₂: 7.487 × 10¹⁸ at/cm.³

Fig. 13

Radial (left-side) and axial (right-side) cuts of the TRIPOLI-4® model of LOENIEv2 in the PF1B configuration for DN measurement—the neutron beam is orientated downwards in the left picture

The neutron source was homogeneously distributed in the inner volume of the source container. The anisotropy of the source emission was distributed over 18 angular directions, according to tabulated values given by NPL. The energy spectra of the different sources were taken from the reference, based on ISO standards [43] (AmBe, AmB, AmF, Cf sources) or from NPL spectrum measurement (AmLi source).

The individual efficiency of each PC was estimated from the ³He(n,p) reaction rate in the active volume of each tube. We present in Table 5 the comparison of the simulated and measured efficiency.

Table 5 Comparison of the simulated efficiency with the measured values (TRIPOLI-4/JEFF-3.3)

The calculated efficiencies $\varepsilon \left(E\right)$ compare very well with the measured values for all the neutron sources, the average [C/E-1] being less than 0.3%. The standard deviation of [C/E-1] values is consistent with [C/E-1] uncertainties, mostly due to the source emission rate calibration.

4.4.3 Calculation of efficiencies for prompt and delayed neutron emission for ²³⁵U thermal fission

The Monte-Carlo model of LOENIEv2 was applied to compute the absolute efficiency for the measurement of delayed and prompt neutron resulting from the thermal fission of ²³⁵U. A detailed model of the MFC target, as well as its connector and cable have been described, in order to account for its scattering and capture effects (see Fig. 19).

Depending on the method used for fission rate calibration, we may require the absolute efficiency ${\varepsilon }_{d}$ from the delayed neutron emission (activation foil, active target or spectroscopy of fission product, see Sects. 2.3.1 to 2.3.3) or the ratio of efficiencies ${{\varepsilon }_{p} /\varepsilon }_{d}$ between the prompt and delayed neutron emission (prompt neutron emission method, see Sect. 2.3.4). Calculations were performed using the energy distributions of delayed and prompt neutrons from the JEFF-3.3 library.

For the uncertainty estimation on ${\varepsilon }_{d}$ and ${\varepsilon }_{p}$, in addition to the 0.6% uncertainty on $\varepsilon \left(E\right)$ resulting from the NPL calibration, we have also accounted for spectrum uncertainties from delayed and prompt neutron emissions. To do so, we apply a Total Monte Carlo approach. Based on the covariance matrix associated to the prompt neutron spectrum, 128 independent ENDF files were produced with a sampling method. These files are loaded in 128 independent runs to estimate the impact of prompt neutron spectrum on the computed efficiency. For delayed neutron emission, as no covariance data exists, we have fitted the equilibrium spectrum (i.e. average of DN group spectra) with a simplified Watt spectrum and have estimated the uncertainty on the ${E}_{a}$ and ${E}_{b}$ parameters from a fit obtained with the CONRAD code. Then 128 independent runs were computed with 128 independent source definitions, based on the sampling of the model parameters. Results of this uncertainty propagation study are presented in Table 6.

Table 6 Uncertainty of the simulated efficiency for prompt and delayed neutron spectra

Due to the almost flat behavior of the efficiency curve between 100 keV and 1 MeV, the propagated uncertainty due to the equilibrium delayed neutron spectrum is negligible and the one of prompt neutron spectrum remains very low. This uncertainty is dominated by the NPL calibration. For the efficiency ratio ${{\varepsilon }_{p} /\varepsilon }_{d}$, the systematic contribution from NPL vanishes and only the uncertainty due to the spectra remains.

In order to account for the small variation of the efficiency curve in the energy range of delayed neutron spectrum, we have computed group-dependent correction factors as ratios ${f}_{k}={\varepsilon }_{d,k}/{\varepsilon }_{d}$, so that Eq. (5) becomes:

$$c\left(t\right)=b\left(t\right)+F\overline{{\nu }_{\text{d}}} {\varepsilon }_{d}\sum_{k=1}^{n}{f}_{k}{a}_{k}(1-{e}^{-{\lambda }_{k}{t}_{i}}){e}^{-{\lambda }_{k}t}$$

(31)

We summarize in Table 7 the values needed for the different methods of fission rate calibration.

Table 7 Efficiency values for prompt neutron emission, equilibrium and group-spectra delayed neutron emission

5 Experimental results at ILL with a 235U target

Once LOENIEv2 was calibrated in efficiency and a valid dead time correction was determined, we can present the DN measurement performed at ILL. Among the important parameters that drive the determination of the physical quantities of interest, we have:

• the background counting rate,

• the irradiation and cycle times,

• the fission rate.

These different key ingredients of the DN equations are discussed in the next sections.

5.1 Background measurements

Two types of background are considered in the analysis.

The first type of background corresponds to the “beam on” situation, noted ${b}_{on}$. The latter is obtained with a dummy MFC instead of the fissile one, irradiated by the neutron beam. This background source is mostly due to the interaction of thermal neutrons with the beam stop of the PF1B experimental area and with the boron rubber covering the LOENIEv2. Indeed, ¹⁰B(n_th,α) reactions can be followed by ¹⁰B(α,n) and ¹¹B(α,n) reactions, which produce fast neutrons of mean energy ~ 2 MeV [25, 39]. In addition to this, TRIPOLI-4 calculations were performed to verify that the contribution of the fissile deposit does not provide an additional background counting rate, especially due to neutron elastic scattering. While 5 meV neutrons can be up-scattered to a higher energy, they still have a huge probability to be stopped by the boron rubber covering the inner channel of LOENIEv2.

Results of background measurements with the dummy MFC are reported in Table 8. A statistical analysis of the background counting rate with time was conducted. The latter was shown to be stable, without any significant drift. As a consequence, we may consider the standard deviation of the mean as the uncertainty estimate of the mean value for ${b}_{on}$.

Table 8 “Beam on” background counting rate measurement

The difference of counting rate between the two campaigns is due to a change in the experimental configuration regarding the position of the beam stop, which is placed closer to the LOENIEv2 in the ALDEN-3 campaign than in the ALDEN-2 one. However, these values remain small compared to the counting rate due to prompt + delayed neutrons in the irradiation of the MFC (~ 10⁵ c/s).

The second type of background component corresponds to the “beam off” situation, noted ${b}_{off}$. The latter is due to fast neutrons from similar (α,n)-type reactions, on materials used upstream of the experimental set-up, especially the fast shutter composed of B₄C plates and the slow shutter made of borated PE. This background can be determined with the dummy MFC or with the fissile one, as long as the measurement is performed after a sufficient time to let the DN precursors decay. We summarize in Table 9 the results for the “beam off” background counting rate, acquired with the dummy MFC.

Table 9 “Beam off” background counting rate measurement

Under stable conditions of the reactor power, we observe that the background counting rate measured with the MFC, long after the irradiation phase, matches the one measured with the dummy target. However it is determined with a much higher uncertainty, as only 5 s of the 100 s/550 s cycles are used for this purpose.

For the analysis of long DN decays, it is important to ensure that the background counting rate is stable with time. In practice, variations of the background counting rate can occur due to the physics of the reactor (slow power drift, power drops due to unexpected events…) or due to electromagnetic perturbations of the surrounding instruments in the same hall. One way to control the stability of the background is to analyze the last seconds in experiments of long counting times. Indeed, for decay periods higher than 400 s, the DN counting rate reaches less than 1% of the background counting rate. Based on a rough estimation of the remaining DN and subtracting it from the overall counting rate, it is possible to have an estimation of the background counting rate dependence with time, in time intervals corresponding to the cycle time. In Fig. 14, an example of this analysis is illustrated for two sets of data.

Fig. 14

Background counting rate as a function of time (each point is recorded after a cycle time of 500 s)

While runs [4738–4797] show a stable behavior with time, we observe a slow drift in the [6241–6279] series. Considering the amount of recorded data with many redundant cycles, it is chosen to discard this second series in order to keep the data for which a stable background counting rate is observed.

5.2 Irradiation and cycle time determination

Irradiation times (${t}_{on}$) and cycle times (${t}_{on}+ {t}_{off})$ were accurately measured thanks to the time stamp recording of the photodiode signal, generated at each rotation of the fast shutter (open or close). These values directly impact the determination of the $\overline{{\nu }_{\text{d}}}$ from Eq. (8), as well as the fission rate through Eq. (20).

We summarize in Table 10 the results obtained for the two experiments for DN yield measurement and in Table 11 the ones for the DN group parameter measurement. Average values and standard deviations for the irradiation and cycle times are determined from the probability distribution of ${t}_{on}$ and ${t}_{on}+{t}_{off}$ over the distribution of cycles.

Table 10 Irradiation and cycle times in ${\upnu }_{d}$ measurements

Table 11 Irradiation and cycle times in $({\uplambda }_{k},{a}_{k})$ measurements

5.3 Fission rate measurement

We summarize in Table 12 the run numbers associated to the different fission rate measurement methods.

Table 12 Run list for fission rate measurements

Three of the four methods are associated to the same experiment (run No. 3892) and can be directly compared. For the post-irradiation spectroscopy realized only in the ALDEN-1 campaign, fission rate results are rescaled to the irradiation flux of the ALDEN-3 campaign.

5.3.1 Active target signal method

The measurement of the MFC in run No. 6892 provided a raw counting rate of 2.35 10⁵ c/s. This value was corrected by three factors:

• (a) a dead time correction based on a non-extendable model,

• (b) non-linearity effects between the ³He counting rate and the MFC counting rate,

• (c) an intrinsic efficiency factor to account for the charge collection deficit and fission product self-attenuation within the fissile deposit.

Factor (a) was computed with τ = 100 ± 10 ns, which correspond to the duration of the TTL signal generated from the pulse processing of the MFC signal. The uncertainty on this correction is 0.24%.

Factor (b) was determined lately during the ALDEN-3 experimental campaign by modulating the incoming neutron flux from 3 to 100%, thanks to the fast shutter. A correction factor was determined between the ³He counting rate measured for Run No. 3892, and its extrapolation for a counting rate of 0 in ideal conditions. It is determined to be $C=1+{c}_{NL}=$ 1.077. We arbitrary assume a 10% relative uncertainty on the ${c}_{NL}$ term.

Factor (c) was the hardest one to determine. It is usually the result of a complex calibration procedure, using a standard neutron field in a thermal column or in a pure fission spectrum, like the ones provided by the BR-1 facility [46]. For the MFC used in this experiment, the deposited mass is quite low (400 µg / cm²) and we can try to estimate this efficiency based on the extrapolation of the PHA spectrum (see Fig. 15).

Fig. 15

PHA distribution of the signal provided by the ²³⁵U MFC at low counting rate (2.25 10.³ c/s)

The intrinsic efficiency measures the fraction of detected signal for each fission event. It can be determined from the ratio between the peak integral ($I$) and the overall spectrum integral ($I+A$), including the discarded counts. Below an amplitude value of 80 channels, we observed a significant increase of the counting rate due to a mix of alpha and gamma detections, on top of electronic noise. The fission product spectrum is assumed to tend to 0, as presented in the figure. As the exact form of the extrapolation is unknown, we determine an intrinsic factor 0.984 with an arbitrary uncertainty of 1%.

Combining the three factors, we end up with a corrected fission rate estimation for Run No. 3892 of 2.631 10⁵ s⁻¹ with an uncertainty of 1.3%.

5.3.2 Activation foil method

An activation foil of Al-Au alloy, containing 0.1% in ¹⁹⁷Au was fixed to the front edge of the MFC (see Fig. 16). It is 8 mm in diameter (same as the fissile deposit), 100 µm thick. The corresponding total weight is 13.946 ± 0.001 mg.

Fig. 16

Photo of the Al-Au activation foil for neutron flux calibration

The MFC and its activation foil were irradiated for 4 h. The foil was sent to the LBA (Low Activity Laboratory) of LPSC Grenoble, shortly after the irradiation. The activity was determined to be (1.2480 ± 0.034)10⁴ Bq/g. Accounting for the irradiation time, we estimate a saturated activity (2.97347 ± 0.081)10⁵ Bq/g.

A Monte-Carlo model of the experiment was built, describing the incoming neutron flux as a beam of diameter 15 mm, with the energy distribution provided by [28]. The MFC and its cable were accurately described. The ratio of macroscopic reaction rate of Eq. (17) is determined to be:

$$\frac{{n}_{U235}{\int }{\sigma }_{f,U235}\left(E\right)\phi \left(E\right)dE}{{n}_{Au}{\int }{\sigma }_{c,Au}\left(E\right)\phi \left(E\right)dE} = 70.60 \pm 0.01. $$

Multiplying this ratio with the saturated activity of the activation dosimeter, we determined the fission rate for Run No. 3892 to be 2.928 10⁵ s⁻¹ with an uncertainty of 3.2%. This uncertainty combines the contribution of ²³⁵U mass estimation (± 1.6%), the cross sections uncertainties of ²³⁵U and ¹⁹⁷Au at the mean energy of 5 meV (± 0.7% and ± 0.2% respectively), and the measurement of the post-irradiation gold activity (± 2.7%).

5.3.3 Post-irradiation spectroscopy method

A few weeks after the end of the first ILL campaign, the MFC was shipped to the MADERE platform at Cadarache. A gamma spectrometry of the MFC was performed to measure the activity of long-lived Fission Products (FP) that were accumulated during the whole campaign. Three FP with appropriate properties (half-life of a few tens of days, existence of at least one intense γ-ray with a good knowledge of its emission probability, well-known cumulative fission yield): ¹⁰³Ru (T_1/2 = 39.3 d), ¹⁴⁰Ba (T_1/2 = 12.8 d) and ¹⁴¹Ce (T_1/2 = 32.5 d).

The activity of each FP can be related to the integral of the fission rate during the campaign. As the irradiation flux has been modified after the first day of experiment to improve the counting statistics, and because the reactor of ILL has some power fluctuations to adjust continuously, it is important to describe the actual profile of fission rate with time. Discretizing the irradiation time in different irradiation steps of fission rate ${F}_{k}$ and duration ${t}_{i,k}$, then, the numbers of counts ${N}_{\gamma }$ recorded in the FP photopeak during a live time ${t}_{a}$ is given by:

$$\begin{aligned}\frac{{N}_{\gamma }}{{t}_{a}}&={Y}_{c}{\eta }_{\gamma }{I}_{\gamma }\frac{1-\text{exp}\left(-\lambda {t}_{m}\right)}{\lambda {t}_{m}}\sum_{k}{F}_{k}\\ &\qquad \text{exp}\left(-\lambda {t}_{d,k}\right)(1-\text{exp}\left(-\lambda {t}_{i,k}\right))\end{aligned}$$

(32)

By normalizing this equation to the fission rate $F$ during the activation foil experiment (Run No. 3892), we obtain:

$$F=\frac{\frac{{N}_{\gamma }}{{t}_{a}}}{{Y}_{c}{\eta }_{\gamma }{I}_{\gamma }\frac{1-\text{exp}\left(-\lambda {t}_{m}\right)}{\lambda {t}_{m}}\sum_{k}\frac{{F}_{k}}{F}\text{exp}\left(-\lambda {t}_{d,k}\right)(1-\text{exp}\left(-\lambda {t}_{i,k}\right))}$$

(33)

The $\frac{{F}_{k}}{F}$ terms can be approximated by the MFC signal counting rate ratio $\frac{{S}_{k}}{S}$, corrected from the three terms detailed in the previous section.

Then the fission rate estimate of Run No. 3892 becomes:

$$F=\frac{\frac{{N}_{\gamma }}{{t}_{a}}}{{Y}_{c}{\eta }_{\gamma }{I}_{\gamma }\frac{1-\text{exp}\left(-\lambda {t}_{m}\right)}{\lambda {t}_{m}}\sum_{k}\frac{{S}_{k}}{S}\text{exp}\left(-\lambda {t}_{d,k}\right)(1-\text{exp}\left(-\lambda {t}_{i,k}\right))}$$

(34)

$S$ and ${S}_{k}$ are respectively the MFC signal counting rate, corrected for dead-time and non-linearity effects, for Run No. 3892 and for Runs from No. 1590 to 2556.

We summarize in Table 13 the fission rate results obtained for the three FP. Cumulative fission yields were taken from the JEFF-3.1.1 library.

Table 13 Fission rate estimate based on the post-irradiation spectroscopy FP

The three FP are consistent within 2σ uncertainty. Due to the strong correlation arising from the efficiency calibration in the data reduction of these 3 FP, a conservative approach is adopted, by considering the results are 100% correlated. Then the weighted average ends up with an uncertainty equal the lowest of the three results.

The fission rate from this method is determined to be 2.904 10⁵ s⁻¹ with an uncertainty of 2.8%.

5.3.4 Neutron emission rate method

The last method we considered is the measurement of the prompt + delayed neutron counting rate from the sixteen PC. Similarly to the DN equations, the measurement of prompt + delayed neutron is written:

$$c\left(t\right)={b}_{on}+\overline{{\nu }_{\text{p}}} {\varepsilon }_{p}F+\overline{{\nu }_{\text{d}}} F\sum_{k}{a}_{k}{\varepsilon }_{k}\left[\left(1-{e}^{-{\lambda }_{k}t}\right)+(1-{e}^{-{\lambda }_{k}{t}_{on}})\frac{1-{e}^{-{\lambda }_{k}({t}_{off}+t)}}{1-{e}^{-{\lambda }_{k}{(t}_{on}+{t}_{off})}}\right]$$

(35)

Then the fission rate is obtained by the integral of this equation over a time range of ${t}_{on}$:

$$F=\frac{{c}_{on}-{b}_{on}}{\begin{array}{c}\overline{{\nu }_{\text{p}}} {\varepsilon }_{p}+\overline{{\nu }_{\text{d}}} \sum_{k}{a}_{k}{\varepsilon }_{k}\\ \left[1-\frac{1-{e}^{-{\lambda }_{k}{t}_{on}}}{{\lambda }_{k}{t}_{on}}(1-\frac{1-{e}^{-{\lambda }_{k}{t}_{on}}}{1-{e}^{-{\lambda }_{k}{(t}_{on}+{t}_{off})}}{e}^{-{\lambda }_{k}{t}_{off}})\right]\end{array}}$$

(36)

${c}_{on}$ and ${b}_{on}$ are the average counting rate during the time range ${t}_{on}$, corrected for dead-time, for respectively the fissile MFC and the dummy one. They are respectively evaluated from Run No. 3892 and Run No. 6420. From this method, we determine a fission rate of (2.901 ± 0.019)10⁵ s⁻¹.

Obviously the fission rate is correlated to the knowledge of $\overline{{\nu }_{\text{d}}}$, while $F$ is supposed to be determined first to obtain $\overline{{\nu }_{\text{d}}} .$ However the impact of any error on $\overline{{\nu }_{\text{d}}}$ remains very low as $\overline{{\nu }_{\text{d}}}$ is roughly 0.65% of the value of $\overline{{\nu }_{\text{p}}}$. A conservative 5% uncertainty was adopted on $\overline{{\nu }_{\text{d}}}$. $\overline{{\nu }_{\text{p}}}$ was taken from JEFF-3.3: 2.409 ± 0.006.

5.3.5 Final recommended fission rate value

The four estimates of the fission rate are compared together on Fig. 17. The horizontal grey line represent the weighted average of the three last methods. The uncertainty is the combined standard deviation of the mean, assuming the three results are independent. The MFC signal method provides a fission rate value lower by 10% compared to the other methods.

Fig. 17

Comparison of fission rate methods

The other methods are 1σ consistent and conclude that the prompt neutron emission method is the most accurate one. It is also the most robust method as it provides a way to record the fission rate fluctuation in real time, contrary to the two other methods. As the weighted average is very close to the prompt neutron emission method, the latter will be kept as the reference value afterwards.

5.4 Determination of delayed neutron decay curves

The production of DN decay curve is realized with MATLAB scripts, chaining the steps described in §4.1. The processing can be easily automatized but the time structure depends on which type of irradiation is considered.

For short decay times dedicated to DN yield measurement (300 or 500 ms), we consider a time structure with a constant δt = 1 ms. For long decay cycles dedicated to DN group parameter measurement, a variable time structure is defined so that relative derivate of the DN counting rate is constant for any time bin $[{t}_{i};{t}_{i+1}]$:

$${t}_{i+1}={t}_{i}+\delta \frac{{\sum }_{k=1}^{8}{a}_{k}\cdot \left(1-{e}^{-{\uplambda }_{k}{t}_{on}}\right)\cdot {e}^{-{\uplambda }_{k}{t}_{i}}}{{\sum }_{k=1}^{8}{a}_{k}\cdot {\uplambda }_{k}.\left(1-{e}^{-{\uplambda }_{k}{t}_{on}}\right)\cdot {e}^{-{\uplambda }_{k}{t}_{i}}}$$

(37)

The parameter ${\varvec{\updelta}}$ is the relative change of DN counting rate from one bin to the next. The lower it is, the larger the time grid will be. This parameter is adjusted as a compromise between a sufficiently large number of points to correctly follow the decay of the 8 exponential terms of the DN model and a sufficiently low one to avoid numerical convergence issues in the fitting performed by the CONRAD code. Typical values for $\updelta$ are 1 to 2%, resulting in a few hundreds of time bins.

We present in Fig. 18 two examples of DN decay curves for short-type cycles (5 s / 0.5 s for DN yield measurement) and long-type cycles (100 s / 500 s for DN group constant measurements). In both cases, a δt = 1 ms was chosen in the transient period between the instant of the beam shutter closing and the start of the DN recording (usually 30 ms). This period corresponds to the time of flight of a tail of very low energy neutrons (typically < 100 µeV) from the shutter position to LOENIEv2 (around 2 m downstream).

Fig. 18

Decay curve for DN counting rate, in 5 s / 0.5 s cycles (left-side) and 100 s / 500 s cycles (right side)

5.5 Delayed neutron yield estimation

The fitting of the DN curve was performed according to the following theoretical model, combining Eqs. (12) and (36):

$$c\left(t\right)={b}_{off}+\overline{{\nu }_{\text{d}}} \frac{\frac{{c}_{on}-{b}_{on}}{\sum_{k=1}^{n}{a}_{k}}\sum_{k=1}^{n}\frac{1-{e}^{-{\lambda }_{k}{t}_{on}}}{1-{e}^{-{\lambda }_{k}({t}_{on}+{t}_{off})}}{\varepsilon }_{d,k}{a}_{k}{e}^{-{\lambda }_{k}t}}{\overline{{\nu }_{\text{p}}} {\varepsilon }_{p}+\overline{{\nu }_{\text{d}}} \sum_{k}{a}_{k}{\varepsilon }_{k}\left[1-\frac{1-{e}^{-{\lambda }_{k}{t}_{on}}}{{\lambda }_{k}{t}_{on}}(1-\frac{1-{e}^{-{\lambda }_{k}{t}_{on}}}{1-{e}^{-{\lambda }_{k}{(t}_{on}+{t}_{off})}}{e}^{-{\lambda }_{k}{t}_{off}})\right]}$$

(38)

The processed data were formatted in a CONRAD input file, in a matrix of time, counting rate and standard deviation. 30 ms following the beam interruption data were discarded, based on the measurement of time needed to reach the background counting rate for the dummy MFC. The experimental values $c\left(t\right)$ are assumed to be independent within one cycle, as well as from one cycle to the next, a reasonable assumption as the only systematic contribution is due to the dead-time correction which is negligible for DN counting.

The fitting was performed with three sets of $({\uplambda }_{{\varvec{k}}}, {\text{a}}_{{\varvec{k}}})$ parameters, in order to test their influence on the determination of $\overline{{\nu }_{\text{d}}}$ : the Keepin data in 6-group [21], the JEFF-3.1.1 data based on the same source but expanded in 8-group [47] and the Foligno 8-group set based on summation calculations [3].

A sensitivity analysis was performed to adjust the fitting range, as a compromise between the maximization of the counting statistics and the minimization of the model correction due to DN decay. The CONRAD uncertainty analysis based on the marginalization technique is used to propagate the systematic uncertainty due to $({\uplambda }_{{\varvec{k}}}, {\text{a}}_{{\varvec{k}}})$, in comparison with the statistical uncertainty due to the counting statistics [48]. Results of this analysis are reported in Table 14.

Table 14 Sensitivity analysis of the fitting range on the determination of ${\upnu }_{d}$ (runs [3868–4658])

The change of ${\nu }_{d}$ value is consistent with the combination of statistical and systematic uncertainties. The best compromise in this study is the 30–130 ms range for which the systematic uncertainty reaches a minimum. Then we present in Table 15 the finalized results for ${\nu }_{d}$.

Table 15 Fitting of the delayed neutron yield

The values derived from the two campaigns are consistent regarding the statistical uncertainties of each one. Although the TT settings were quite different between the two campaigns (800 LSB in ALDEN-2 versus 450–550 LSB in ALDEN-3), the auto-normalisation provided by the prompt neutron emission method ensures a high reproducibility in the estimated DN yield. The following value is finally adopted:

$\overline{{\nu }_{\text{d}}}=$ (1.625 ± 0.010) %.

5.6 Estimation of the delayed neutron group parameters

The decay curves were fitted according to the same model as Eq. (36) with the following modification:

$$c\left(t\right)={b}_{off}+\overline{{\nu }_{\text{d}}}\frac{\frac{{c}_{on}-{b}_{on}}{\sum_{k=1}^{n}{a}_{k}}\sum_{k=1}^{n}\frac{1-{e}^{-{\lambda }_{k}{t}_{on}}}{1-{e}^{-{\lambda }_{k}({t}_{on}+{t}_{off})}}{\varepsilon }_{d,k}{a}_{k}{e}^{-{\lambda }_{k}t}}{\overline{{\nu }_{\text{p}}}{\varepsilon }_{p}+\overline{{\nu }_{\text{d}}}\sum_{k}{a}_{k}{\varepsilon }_{k}\left[1-\frac{1-{e}^{-{\lambda }_{k}{t}_{on}}}{{\lambda }_{k}{t}_{on}}(1-\frac{1-{e}^{-{\lambda }_{k}{t}_{on}}}{1-{e}^{-{\lambda }_{k}{(t}_{on}+{t}_{off})}}{e}^{-{\lambda }_{k}{t}_{off}})\right]}\left(1+A(1-\sum_{k=1}^{n}\left|{a}_{k}\right|)\right)$$

(39)

The additional term in the right bracket provides a constraint in the fitting algorithm to ensure that the ${a}_{k}$ parameters remain always positive and that the sum tends to unity. $A$ is a constant term, selected to adjust the constrain of the ${a}_{k}$ sum to unity. It is taken arbitrary to $A$=10³. This method is an alternative to the common approach of removing one ${a}_{k}$ value (index $j$) among the 8 fitted parameters, and replacing by ${a}_{j}$= $1-\sum_{k\ne j}{a}_{k}$. Our approach has the advantage to avoid an arbitrary choice of which parameter should be removed.

Guess values for the ${a}_{k}$ fitted were taken to 0.125. By avoiding to give an initial guess close to the final fitted values, we can test the robustness of the fitting procedure and how much the final values depend on the initial conditions.

The fitting of the 10 experimental files can be done in two different ways by the CONRAD code:

• By an iterative approach: this method consists of fitting each decay curve successively, by passing the output fitted parameters of experimental file i as input parameters to fit the experimental file i + 1,

• By a combined approach: this method consists of fitting the decay curves altogether, minimizing the sum 10 of the χ² values.

Both approaches were compared, showing minor differences on the final ${a}_{k}$ fitted values, covered by standard deviations. However, the combined approach is preferred to the iterative one because it avoids a more complex uncertainty propagation for the correlated parameters used in the fitting of each decay curve. For instance, the normalization uncertainty due to $\overline{{\nu }_{\text{d}}}$ may be counted several times in the iterative approach while it is shared among the different decay curves in the combined approach.

We present in Figs. 19, 20, 21 various examples of fitted models compared with experimental data for three different decay curves. The plot for normalized residuals do not exhibit any trend, meaning that a consistent set of.

Fig. 19

Fitting of the 100 s / 500 s decay curve (ALDEN-3, runs [3451–3719])

Fig. 20

Fitting of the 15 s / 350 s decay curve (ALDEN-2, runs [4951–5048])

Fig. 21

Fitting of the 1 s/1 s decay curve (ALDEN-2, runs [5059–5298])

${a}_{k}$ parameters was found to fit the 10 different decay curves.

Final estimated values for ${a}_{k}$ with their standard deviation and correlation matrix are presented in Table 16.

Table 16 Fitted group parameters and correlations

5.7 Discussions

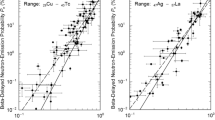
Our DN yield values are compared with the reported data, summarized by the IAEA CRP-group [2] on beta-delayed neutron emission (see Fig. 22). The red shaded line corresponds to the Tuttle evaluation [49], based on the experimental available in 1979, from which the following value was recommended:

$$\overline{{\nu }_{\text{d}}}= (1.621 \pm 0.050) \%$$

Fig. 22

DN yields from the literature compared to values issued by the ALDEN collaboration (Foligno et al. and this work)

Among the nuclear data community, this value is still referred as the most reliable evaluation for the DN yield in ²³⁵U thermal neutron induced fission. Indeed, Tuttle did a comprehensive and careful analysis of the different available data at that time, revising normalization factors and potential errors in reported values. More recent reported values from Blachot or Parish are only other evaluation exercises, without any new measured data.

The value derived from this work matches perfectly with the Tuttle recommendation with a significant reduction of the uncertainty. This was possible thanks to our precise fission rate measurement (< 1%), which is usually the dominant source of uncertainty in other DN yield measurements.

DN group parameters are plotted against datasets from different origins:

• the CRP recommended values [2], which are based on the measurement performed by Piksaikin et al. at IPPE Obninsk [50],

• the CRP estimation based on up-to-date summation calculations [2], using the CRP + ENDF/BVIII.0 decay data for neutron emission probability and half-life, in combination with the JEFF-3.1.1 fission yields,

• the evaluation from the JEFF-3.3 nuclear data library, which is based on the Keepin et al. measurement [51], expending in 8 groups with the Spriggs technique.

The comparison is plotted in Fig. 23

Fig. 23

Comparison of the ²³⁵U group parameters from this work, compared with evaluated values

The group parameters derived from this work match the CRP recommended evaluation within 2σ uncertainty, as well as the results from the summation method. Group values are also very close to the JEFF-3.3 evaluated data, based on Keepin results. While the standard deviations are mostly higher than CRP or JEFF-3.3 evaluations, the propagation of these uncertainties by taking into account the correlation matrix ends up to a much lower uncertainty on the average lifetime ${T}_{1/2}$, as can be seen in Table 17.

Table 17 Comparison of ${T}_{1/2}$ values derived from various evaluations

The ENDF/B-VIII.0 value comes without uncertainty as it is derived from summation calculations by Brady & England from the 1980s [52]. The JEFF-3.3 value has a 5.7% relative uncertainty, essentially due to the lack of correlation matrix between the group parameters. Our ${T}_{1/2}$ value is consistent with the CRP recommended evaluation, within 1σ uncertainty. Note that the values from our work was derived with a 8-group model while the CRP value results from an expansion of the 6-group data in 8-group, using the Spriggs technique. The relevance of this method for uncertainty estimation is questionable and was pointed out by the author of this technique [8] under the terms “It should be noted, however, that the uncertainty of the individual abundances in the LSF may not be physically meaningful”.

6 Conclusions

An experimental setup was settled within a collaborative framework for an accurate measurement of both the DN yield and group parameters. It consists in long counter detector surrounding a fissile target in the form of a MFC, coupled with two fast and efficient beam shutters that can produce cycle irradiations of various durations.

The current paper sums up the methodology of data reduction, from the acquisition of the raw data up to the derivation of the DN macroscopic data. It was applied to the case of the thermal neutron induced fission of ²³⁵U, obtained with the PF1B instrument of ILL.

Among the main achievements of this work, we may emphasize the following points:

• The dead-time of each ³He PC was accurately measured, thanks to dedicated experiments using the D/T accelerator of the GENESIS platform at LPSC, and later confirmed using the ring ratio method at ILL. A value of τ= 7.61 ± 0.07 µs was adopted.

• The LOENIEv2 long counter efficiency was measured thanks to calibrated neutron sources at the NPL. The latter were used to validate a Monte-Carlo model of the long counter, for which a bias as low as 0.2% was obtained, with an uncertainty of 0.6%, using the JEFF-3.3 nuclear data library. The application of this model to estimate the efficiency for DN leads to efficiency values of 20.3% for DN counting and 19.2% for PN counting. The relative variation from one DN group to another is less than 1%, confirming the design calculations of LOENIEv2 in order to flatten the efficiency curve over the 100 keV – 1 MeV energy range

• Four independent techniques were used to measure the fission rate of the ²³⁵U sample. Three of them, i.e. prompt neutron counting, gamma spectrometry of FP and activation foil method, provide consistent results within 1σ uncertainty. The fourth one, based on the MFC counting rate, provides a 10% lower value, due to a rough estimation of the intrinsic efficiency. The prompt neutron counting method provides a much lower uncertainty (0.7%), compared with the two other techniques which are commonly used in other similar experiments. The success of this method and its robustness is the key for a reliable DN yield value estimation and low uncertainty.

The final adopted value for the DN yield in the thermal neutron induced fission of ²³⁵U is $\overline{{\nu }_{\text{d}}}$ = (1.625 ± 0.010) %. This value matches perfectly the Tuttle evaluation of (1.62 ± 0.05) %, and comes with a much lower uncertainty. The group parameters in the 8-group model of Spriggs matches the most recent IAEA recommendations, providing an average lifetime of DN of ${T}_{1/2}$ = (8.87 ± 0.10) s. The significantly reduced uncertainty on this parameter, will be of benefit to the dynamic reactivity estimation based on the inhour equation, for which an uncertainty of 5 to 6% is currently obtained for instance with the latest JEFF-3.3 evaluation.

More results will be published in the near future, based on the same experimental set-up and methodology for the thermal neutron induced fission of ²³⁹Pu and ²³³U and fast neutron induced fission of ²³⁸U. These results will support revised evaluation for the future release of the JEFF-4.0 library, including covariance data on both the DN yield and group constants, which are currently missing from most international nuclear data libraries.