Abstract
The electroweak (EW) sector of the Minimal Supersymmetric Standard Model (MSSM) can account for variety of experimental data. The lighest supersymmetric particle (LSP), which we take as the lightest neutralino, \({\tilde{\chi }}_{1}^0\), can account for the observed Dark Matter (DM) content of the universe via coannihilation with the next-to-LSP (NLSP), while being in agreement with negative results from Direct Detection (DD) experiments. Owing to relatively small production cross-sections a comparably light EW sector of the MSSM is also in agreement with the unsuccessful searches at the LHC. Most importantly, the EW sector of the MSSM can account for the persistent \(3-4\,\sigma \) discrepancy between the experimental result for the anomalous magnetic moment of the muon, \((g-2)_\mu \), and its Standard Model (SM) prediction. Under the assumption that the \({\tilde{\chi }}_{1}^0\) provides the full DM relic abundance we first analyze which mass ranges of neutralinos, charginos and scalar leptons are in agreement with all experimental data, including relevant LHC searches. We find an upper limit of \(\sim 600 \,\, \mathrm {GeV}\) for the LSP and NLSP masses. In a second step we assume that the new result of the Run 1 of the “MUON G-2” collaboration at Fermilab yields a precision comparable to the existing experimental result with the same central value. We analyze the potential impact of the combination of the Run 1 data with the existing \((g-2)_\mu \) data on the allowed MSSM parameter space. We find that in this case the upper limits on the LSP and NLSP masses are substantially reduced by roughly \(100 \,\, \mathrm {GeV}\). This would yield improved upper limits on these masses of \(\sim 500 \,\, \mathrm {GeV}\). In this way, a clear target could be set for future LHC EW searches, as well as for future high-energy \(e^+e^-\) colliders, such as the ILC or CLIC.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
One of the most important tasks at the LHC is to search for physics beyond the Standard Model (SM). This includes the production and measurement of the properties of Cold Dark Matter (CDM). These two (related) tasks will be among the top priority in the future program of high-energy particle physics.
The high-energy searches are complemented by low-energy experiments that search either for rare beyond the SM (BSM) decays, or for small deviation of known SM processes from their SM prediction. Concerning the latter the anomalous magnetic moment of the muon, \((g-2)_\mu \) plays a prominent role. The experimental result deviates from the SM prediction by \(3-4\sigma \) [1, 2]. Improved experimental results are expected in the course of 2020 by the publication of the Run 1 data of the “MUON G-2” experiment [3].
Another clear sign for BSM physics is the precise measurement of the CDM relic abundance [4]. A final set of related constraints comes from CDM Direct Detection (DD) experiments. The LUX [5], PandaX-II [6] and XENON1T [7] experiments provide stringent limits on the spin-independent DM scattering cross-section, \(\sigma _p^{\mathrm{SI}}\).
Among the BSM theories under consideration the Minimal Supersymmetric Standard Model (MSSM) [8,9,10,11] is one of the leading candidates. Supersymmetry (SUSY) predicts two scalar partners for all SM fermions as well as fermionic partners to all SM bosons. Contrary to the case of the SM, in the MSSM two Higgs doublets are required. This results in five physical Higgs bosons instead of the single Higgs boson in the SM. These are the light and heavy \({\mathcal{CP}}\)-even Higgs bosons, h and H, the \({\mathcal{CP}}\)-odd Higgs boson, A, and the charged Higgs bosons, \(H^\pm \). The neutral SUSY partners of the (neutral) Higgs and electroweak gauge bosons gives rise to the four neutralinos, \({\tilde{\chi }}_{1,2,3,4}^0\). The corresponding charged SUSY partners are the charginos, \({\tilde{\chi }}_{1,2}^\pm \). The SUSY partners of the SM leptons and quarks are the scalar leptons and quarks (sleptons, squarks), respectively.
The electroweak (EW) sector of the MSSM, consisting of charginos, neutralinos and scalar leptons can account for a variety of experimental data. Concerning the CDM relic abundance, the MSSM offers a natural candidate, the Lightest Supersymmetric Particle (LSP), the lightest neutralino, \({\tilde{\chi }}_{1}^0\) [12, 13], while being in agreement with negative results from DD experiments. On the other hand, the unsuccessful searches at the LHC can be attributed to the rather small production cross-sections, keeping a relatively light EW sector of the MSSM well alive. Most importantly, the EW sector of the MSSM can account for the persistent \(3-4\,\sigma \) discrepancy of \((g-2)_\mu \).
Various articles have investigated (part of) this interplay. The impact of LHC Run I searches in particular on the chargino/neutralino sector of the MSSM have been discussed, among others, in [14,15,16], and including Run II prospects in [17, 18]. A combination of Run I and (then) current \((g-2)_\mu \) data can be found in [19, 20] while the \((g-2)_\mu \) without the LHC constraints were discussed in [21, 22]. Compressed chargino/neutralino spectra that are difficult to access at the LHC in the context of DM bounds were discussed in [23]. The direct searches at the LHC Run I, the (then) current \((g-2)_\mu \) deviation from its SM prediction, the measurement of the CDM relic abundance and the limits from CDM DD experiments have been analyzed in a global fit to the phenomenological MSSM with 11 parameter (pMSSM11 [24]) in [25]. It was found that this model “easily” satisfies all the constraints together. LHC Run II data, the (then) current bound from \((g-2)_\mu \) as well as DM constraints were analyzed in several benchmark planes in [26,27,28] and in two benchmark scenarios w.r.t. the DM relic abundance in [29]. In the latter the relevant LHC searches have been applied without a proper re-casting. All Run II data, again without proper re-casting, but with DM data, was taken into account in [30], favoring models with relatively heavy sleptons. Run II data for chargino/neutralino searches with some DM implications has also been presented in [31, 32].
The aim of the paper is two-fold. Under the assumption that the \({\tilde{\chi }}_{1}^0\) provides the full DM relic abundance we first analyze which mass ranges of neutralinos, charginos and sleptons are in agreement with all relevant experimental data. Concerning the LHC searches we include all relevant existing data, mostly relying on re-casting via CheckMATE [33,34,35]. In a second step we assume that the new result of the Run 1 of the “MUON G-2” collaboration at Fermilab yields a precision comparable to the existing experimental result with the same central value. We analyze the potential impact of the combination of the Run 1 data with the existing result on the allowed MSSM parameter space. The results will be discussed in the context of the upcoming searches for EW particles at the HL-LHC. We will also comment on the discovery prospects for these particles at possible future \(e^+e^-\) colliders, such as the ILC [36, 37] or CLIC [37,38,39,40].
2 The electroweak sector of the MSSM
Here we briefly review the EW sector of the MSSM, consisting of charginos, neutralinos and scalar leptons. The scalar quark sector is assumed to be heavy and not to play a relevant role in our analysis. Throughout this paper we also assume that all parameters are real, i.e. the absence of \(\mathcal{CP}\)-violation.
MSSM neutralinos are the linear superpositions of the neutral \(SU(2)_L\) and \(U(1)_Y\) gauginos and neutral higgsinos \({\tilde{B}}, \tilde{W^3}\), \({\tilde{H}}_{u}^{0}\) and \({\tilde{H}}_{d}^{0}\), respectively. Their masses and mixings are determined by \(U(1)_Y\) and \(SU(2)_L\) gaugino masses \(M_1\) and \(M_2\), the Higgs mixing parameter \(\mu \) and \(\tan \beta \), the ratio of the two vacuum expectation values (vevs) of the two Higgs doublets of MSSM, \(\tan \beta = v_2/v_1\). The neutralino mass matrix in the basis \((-i {\tilde{B}}, -i {\tilde{W}}^3, {\tilde{H}}_{u}^{0}, {\tilde{H}}_{d}^{0} )\) is given by
where \(c_\beta (s_\beta )\) denotes \(\cos \beta (\sin \beta )\) and \(c_\mathrm {w}= \sqrt{1 - s_\mathrm {w}^2} = M_W/M_Z\) denotes effective weak leptonic mixing angle, with \(M_W(M_Z)\) being the mass of the W (Z) boson. After diagonalization, the four eigenvalues of the matrix give the four neutralino masses \(m_{{\tilde{\chi }}_{1}^0}< m_{{\tilde{\chi }}_{2}^0}< m_{{\tilde{\chi }}_{3}^0} <m_{{\tilde{\chi }}_{4}^0}\). As discussed above, the lightest neutralino, \({\tilde{\chi }}_{1}^0\) is the LSP and is assumed to yield the full CDM relic density, see Sect. 3.3 below.
The chargino mass eigenstates result as a mixing between the charged winos and higgsinos \((\tilde{W^\pm }, {\tilde{H}}_{u/d}^{\pm })\) respectively with their mass matrix given by,
Diagonalizing \(M_C\) with a bi-unitary transformation, two chargino-mass eigenvalues \(m_{{\tilde{\chi }}_{1}^\pm } < m_{{\tilde{\chi }}_{2}^\pm }\) can be obtained.
For the sleptons, as will be discussed below, we choose common soft SUSY-breaking parameters for all three generations. The charged slepton mass matrix can be written as,
where
Here \(l = e, \mu , \tau \) and \(m_{{\tilde{l}}_L}\) and \(m_{{\tilde{l}}_R}\) are the left- and right-slepton mass input parameters, \(I^{3L}_l\) and \(Q_l\) denote the weak isospin and electric charge of the lepton \(l = e, \mu , \tau \). We take the trilinear coupling \(A_l\) to be zero for all the three generations of leptons. Thus the off-diagonal term \(m_l X_l\) is given by \(m_l \mu \tan \beta \), and hence the mixing is significant only for the third generation. Thus, for the first two generations, the mass eigenvalues can be approximated as \(m_{{\tilde{l}}_{1}} \simeq m_{LL}, m_{{\tilde{l}}_{2}} \simeq m_{RR}\). In general we follow the convention that \({\tilde{l}}_1\) (\({\tilde{l}}_2\)) has the large “left-handed” (“right-handed”) component. Besides the symbols equal for all three generations, we also explicitly use the scalar electron, muon and tau masses, \(m_{{\tilde{e}}_{1,2}}\), \(m_{\tilde{\mu }_{1,2}}\) and \(m_{\tilde{\tau }_{1,2}}\).
The sneutrino and slepton masses are connected by the usual MSSM mass relation:
Thus, overall the EW sector at the tree level can be described with the help of six parameters: \(M_1,M_2,\mu , \tan \beta , m_{{\tilde{l}}_L}, m_{{\tilde{l}}_R}\). Throughout our analysis we neglect \({\mathcal{CP}}\)-violation and assume \(\mu , M_1, M_2 > 0 \). From general considerations, even sticking to real parameters, one could choose some (or all) of the mass parameters negative. However, it should be noted that the results for physical observable are affected only by certain combinations of signs (or phases in general). It is possible, for instance, to rotate the phase of \(M_2\) away, i.e. choose (real and) \(M_2 > 0\). This leaves in principle the signs of \(M_1\) and \(\mu \) free. However, one of the main constraints we will take into account is the anomalous magnetic moment of the muon, \(a_\mu := (g-2)_\mu /2\), see Sect. 3.2. Having \(M_1\), \(M_2\) and \(\mu \) positive yields in general a positive contribution to \(a_\mu \), as it is required by experimental data (see Sect. 3.2). Changing one or both signs of \(M_1\) and \(\mu \) negative yields a substantially reduced or even negative contribution to \(a_\mu \). Consequently, having this constraint in mind, our choice of only positive values is justified (see, however, the discussion in Sect. 7).
2.1 The other MSSM sectors
Following the stronger experimental limits from the LHC [41, 42], we assume that the colored sector of the MSSM is sufficiently heavier than the EW sector, and does not play a role in this analysis. For the Higgs-boson sector we assume that the radiative corrections to the light \({\mathcal{CP}}\)-even Higgs boson (largely originating from the top/stop sector) yield a value in agreement with the experimental data, \(M_h\sim 125 \,\, \mathrm {GeV}\). This naturally yields stop masses in the TeV range [43], in agreement with the above assumption. Concerning the Higgs-boson mass scale, as given by the \({\mathcal{CP}}\)-odd Higgs-boson mass, \(M_A\), we employ the existing experimental bounds from the LHC. In the combination with other data, this results in a non-relevant impact of the heavy Higgs bosons on our analysis, as will be discussed below.
3 Relevant constraints
In this section we briefly review the experimental constraints that are relevant for the EW sector of the MSSM. They consist of direct searches at the LHC, the \((g-2)_\mu \) deviation from its SM prediction, the measurement of the CDM relic abundance and the limits from CDM DD experiments. A review about the combination of these effects in SUSY (after LHC Run 1) can be found in [25].
3.1 Constraints from the LHC
In the absence of color-sector SUSY particles within the LHC reach, the production of electroweak gauginos (\({\tilde{\chi }}_{1}^+ {\tilde{\chi }}_{1}^-, {\tilde{\chi }}_{1}^\pm {\tilde{\chi }}_{2}^0\)) and sleptons (\({\tilde{l}}_{L,R} {\tilde{l}}_{L,R}\)) are the most important search channels at the LHC. The ATLAS and CMS collaborations have searched for these processes in a variety of final states. The LHC searches are usually interpreted in terms of “simplified” models with specific assumptions on the compositions and branching ratios of the SUSY particles. For example, all the searches described through Eqs. (5)–(9) assume \({\tilde{\chi }}_{1}^\pm / {\tilde{\chi }}_{2}^0\) and \({\tilde{\chi }}_{1}^0\) to be purely wino- and bino-like respectively so that \(m_{{\tilde{\chi }}_{2}^0} = m_{{\tilde{\chi }}_{1}^\pm }\). However, the sensitivity of the searches may vary significantly with the variation of the gaugino-composition as well as mass hierarchy among the SUSY particles.
In this section we summarize the LHC Run-II results that are most relevant for our analyses. A graphical “comparison” of the reach of these various LHC constraints is shown in Fig. 1, as described in detail below. In the left plot we show the different search modes in the \(m_{{\tilde{\chi }}_{1}^0}\)-\(m_{{\tilde{\chi }}_{1}^\pm }\) plane as given in the respective references. In the right plot of Fig. 1, we depict the limits on the \(m_{{\tilde{\chi }}_{1}^0}\)-\(m_{{\tilde{l}}_{1}}\) plane.Footnote 1 As will be argued in Sect. 4.1 and shown explicitly in Sect. 5 we focus on parameter ranges, where either the light chargino or the sleptons are close in mass to \({\tilde{\chi }}_{1}^0\) (\({\tilde{\chi }}_{1}^\pm \)- or \({\tilde{l}}^{\pm }\)-coannihilation).
-
Decay via sleptons (\(\mathbf{3}{{\varvec{l}}}\))
The pair production of electroweak gauginos decaying via the process of Eq. (5) to 3l final states is one of the most promising search channels to look for electroweak SUSY particles at the LHC. Exclusion limits from the ATLAS searches [44] at 36 fb\(^{-1}\) luminosity are based on a “simplified model” assuming that the decay of \({\tilde{\chi }}_{1}^\pm / {\tilde{\chi }}_{2}^0\) proceeds via an intermediate \({\tilde{l}}_L\) or \({\tilde{\nu }}_L\) with 100% branching ratio, with \(m_{{\tilde{l}}_L}= m_{{\tilde{\nu }}_{l}}= (m_{{\tilde{\chi }}_{2}^0} + m_{{\tilde{\chi }}_{1}^0})/2\). This search excludes upto \(m_{{\tilde{\chi }}_{1}^0} \sim 1100 \,\, \mathrm {GeV}\) for \(m_{{\tilde{\chi }}_{2}^0} \lesssim 550 \,\, \mathrm {GeV}\). However, it is sensitive to mass splittings \((m_{{\tilde{\chi }}_{1}^\pm }-m_{{\tilde{\chi }}_{1}^0}) \gtrsim 70 \,\, \mathrm {GeV}\). Thus, this limit is not sensitive to \({\tilde{\chi }}_{1}^\pm \)-coannihilation region which corresponds to much smaller mass-splitting between \({\tilde{\chi }}_{1}^\pm \) and \({\tilde{\chi }}_{1}^0\). We impose this limit on the \(m_{{\tilde{\chi }}_{1}^\pm }-m_{{\tilde{\chi }}_{1}^0}\) plane of \({\tilde{l}}\)-coannihilation region. We show the exclusion contour from ATLAS in Fig. 1a as a red dashed line.
 (5)
(5) -
Decay via sleptons (\(\mathbf{2}{{\varvec{l}}}\))
The decay chain in Eq. (6) refers to the ATLAS searches [45] at 139 fb\(^{-1}\) for \({\tilde{\chi }}_{1}^\pm \)-pair production with subsequent decays through \({\tilde{l}}/{\tilde{\nu }}\). The ATLAS analysis is performed for the specific parameter choice \(m_{{\tilde{l}}} = (m_{{\tilde{\chi }}_{2}^0} + m_{{\tilde{\chi }}_{1}^0})/2\) and is sensitive to mass differences \(\Delta m = (m_{{\tilde{\chi }}_{1}^\pm } - m_{{\tilde{\chi }}_{1}^0}) \gtrsim 50 \,\, \mathrm {GeV}\). Thus, it is not possible to probe the \({\tilde{\chi }}_{1}^\pm \)-coannihilation region with the help of these constraints. As above, we impose these limits on the \(m_{{\tilde{\chi }}_{1}^\pm }-m_{{\tilde{\chi }}_{1}^0}\) plane of the \({\tilde{l}}^{\pm }\)-coannihlation scenario. In Fig. 1a this exclusion limit is shown as a magenta line.
 (6)
(6)The ATLAS limit for the same production and decay mode as in Eq. (6) at 36 fb\(^{-1}\) luminosity given in [44] is shown as a gray dashed line in Fig. 1a. However, this provides a much weaker limit for this scenario. The CMS searches for gaugino-pair production with decay via sleptons/sneutrinos to final states containing two or more leptons can be found in [46].
-
Decay via gauge bosons
The ATLAS searches described by Eqs. (7a)–(8) [44, 45] look for decays of gaugino pairs through on-shell gauge bosons. Thus, for these searches to be effective, the mass difference between \({\tilde{\chi }}_{1}^\pm \) and \({\tilde{\chi }}_{1}^0\) should at least be \(\sim \) electroweak scale, i.e. an on-shell gauge boson is required, which makes them practically insensitive to the \({\tilde{\chi }}_{1}^\pm \)-coannihilation region. On the other hand, these limits can in principle be applied to the \(m_{{\tilde{\chi }}_{1}^\pm }-m_{{\tilde{\chi }}_{1}^0}\) plane of the \({\tilde{l}}^{\pm }\)-coannihlation region. It should be noted that these searches are most effective for scenarios where \(m_{{\tilde{l}}_L}, m_{{\tilde{l}}_R}\) lie above \(m_{{\tilde{\chi }}_{2}^0}, m_{{\tilde{\chi }}_{1}^+}\), so that gaugino-decay via on-shell sleptons are not kinematically accessible.
Reference [44] provides an exclusion contour at 36 fb\(^{-1}\) combining the two channels given in Eq. (7a) and Eq. (7b). This is by far the strongest limit for this kind of scenario. We show the combined contour from ATLAS in Fig. 1a by a cyan dashed line. The various multi-lepton based searches are subdivided as:
-
(a)
3l: The production and decay of the gauginos are expected to proceed as in Eq. (7a).
 (7a)
(7a) -
(b)
\(2l + jets\): The search demands the presence in the signal of two leptons of same flavour and opposite sign (SFOS) from the Z-boson and two or more jets from hadronic decays of the W, following Eq. (7b).
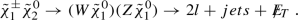 (7b)
(7b) -
(c)
2l: Apart from the above exclusion limit, there exists ATLAS exclusion contours [45] at 139 fb\(^{-1}\) for decay processes like Eq. (8) in final states containing two opposite sign leptons. This is shown by a blue line in Fig. 1a. However, this is much weaker compared to the combined limit mentioned above.
 (8)
(8)Similar searches performed by the CMS collaboration are described in [47].
-
(a)
-
Decay via Higgs boson (\({{\varvec{l, b}}}\)-jets)
There are searches performed by ATLAS [48] at 139 fb\(^{-1}\) (and CMS [49] at 35.1 fb\(^{-1}\)) which look for decays of gaugino pairs through on-shell gauge and Higgs bosons as in Eq. (9). These searches assume 100 % \(\text {BR}\) for the decay mode \({\tilde{\chi }}_{2}^0 \rightarrow h {\tilde{\chi }}_{1}^0\), for a purely wino-like \({\tilde{\chi }}_{2}^0\). This limit is shown as a yellow-dashed line in Fig. 1a.
 (9)
(9) -
\({\tilde{{{\varvec{l}}}}}\) pair production (\(\mathbf{2}{{\varvec{l}}}\))
The ATLAS limit from the searches of slepton pair production in the dilepton final state [45] as described in Eq. (10) is sensitive for mass differences of \((m_{{\tilde{l}}} - m_{{\tilde{\chi }}_{1}^0}) \gtrsim 80 \,\, \mathrm {GeV}\), making it inefficient for \({\tilde{l}}^{\pm }\)-coannihilation region. On the other hand, these limits can give constraints in the \(m_{{\tilde{l}}}-m_{{\tilde{\chi }}_{1}^0}\) plane of our \({\tilde{\chi }}_{1}^\pm \)-coannihilation region. We show this as a magenta line in Fig. 1b. For the same search channel a weaker limit at 36 fb\(^{-1}\) luminosity comes from Ref. [44] which is shown as a red dashed line in Fig. 1b. Corresponding CMS search is described in [50].
 (10)
(10) -
Compressed scenario
Apart from the standard searches mentioned above, there are also dedicated analyses [51] to investigate parameter spaces with compressed mass spectra, where the mass-splittings between \({\tilde{\chi }}_{1}^\pm ,{\tilde{\chi }}_{2}^0,{\tilde{l}}^{\pm }\) and \({\tilde{\chi }}_{1}^0\) can be very low. The ATLAS searches [51] at 139 fb\(^{-1}\) are sensitive to mass-splittings as low as \(\sim \) 1.5 GeV for \(m_{{\tilde{\chi }}_{2}^0} \sim 100 \,\, \mathrm {GeV}\) whereas for sleptons the mass-splitting goes down to \(\sim 550 \,\, \mathrm {MeV}\) for \(m_{{\tilde{l}}_{}} \sim 70 \,\, \mathrm {GeV}\). In these cases, \({\tilde{\chi }}_{1}^\pm \) and \({\tilde{\chi }}_{2}^0\) are expected to decay via off-shell W and Z bosons to final states containing two leptons and
 (i.e. requiring a leptonic
\(Z^*\) decay and a hadronic
\(W^*\) decay), see Eq. (11), whereas for the sleptons the decay process is given in Eq. (12). In both cases, because of the small mass splitting, the two same-flavor opposite-charge leptons in the final state come out to be very soft. Thus, to increase the sensitivity of the searches, the presence of initial-state radiation (ISR) is also required which gives the system some amount of boost. The searches for
\({\tilde{l}}^+{\tilde{l}}^- ({\tilde{\chi }}_{1}^\pm {\tilde{\chi }}_{2}^0)\)-pair production can be applied to constrain
\({\tilde{l}}~({\tilde{\chi }}_{1}^\pm )\)-coannihilation regions. These limits are shown in green both in Fig. 1a, b. Sirunyan et al. [52] describes the corresponding CMS searches targeting the compressed mass spectrum.
(i.e. requiring a leptonic
\(Z^*\) decay and a hadronic
\(W^*\) decay), see Eq. (11), whereas for the sleptons the decay process is given in Eq. (12). In both cases, because of the small mass splitting, the two same-flavor opposite-charge leptons in the final state come out to be very soft. Thus, to increase the sensitivity of the searches, the presence of initial-state radiation (ISR) is also required which gives the system some amount of boost. The searches for
\({\tilde{l}}^+{\tilde{l}}^- ({\tilde{\chi }}_{1}^\pm {\tilde{\chi }}_{2}^0)\)-pair production can be applied to constrain
\({\tilde{l}}~({\tilde{\chi }}_{1}^\pm )\)-coannihilation regions. These limits are shown in green both in Fig. 1a, b. Sirunyan et al. [52] describes the corresponding CMS searches targeting the compressed mass spectrum.  (11)
(11)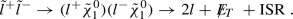 (12)
(12) -
Searches involving stau
The ATLAS collaboration has looked for direct production of \({\tilde{\tau }}\)-pairs in final states involving hadronically decaying \(\tau \)-leptons [53], yielding almost negligible limits for \(m_{{\tilde{\chi }}_{1}^0} > 100 \,\, \mathrm {GeV}\). Although there exists searches by the CMS collaboration [46] looking for decays of \({\tilde{\chi }}_{1}^\pm \) and \({\tilde{\chi }}_{2}^0\) to \(\tau \)-rich final states, there are no similar searches by ATLAS so far. Such limits are effective mostly for parameter regions where decays of \({\tilde{\chi }}_{1}^\pm / {\tilde{\chi }}_{2}^0\) via first two generations of sleptons are not kinematically allowed. As we will see in Sect. 4, in our analysis the mass of the lighter stau lies closely below \(m_{\tilde{e}_{1}}, m_{\tilde{\mu }_{1}}\) and/or \(m_{\tilde{e}_{2}}, m_{\tilde{\mu }_{2}}\) depending on the coannihilation scenario being considered. Therefore the limits from the pair-production of the first two generations of sleptons (Eq. (10)) already put sufficiently stringent limits on the parameter space relevant for stau searches. Moreover, the CMS exclusion limits are sensitive only for mass differences \((m_{{\tilde{\tau }}} - m_{{\tilde{\chi }}_{1}^0}) \gtrsim 30 \,\, \mathrm {GeV}\). Therefore, this limit will not be very sensitive to parameter regions relying solely on stau-coannihilation mechanism to achieve the right relic density value. Keeping these facts in mind we do not explicitly take into account these limits in our analysis.
The constraints imposed on the parameter space of our analysis are summarized in Table 1 and represented “graphically” in Fig. 1 above. As also discussed above, the exclusion contours published by experimental collaborations are based on “simplified model” approach. However, for the SUSY scenarios discussed in our work, the kinematic configurations as well as gaugino-compositions may be significantly different from those analyses, leading to notable change in some of the exclusion limits. Here, we use an independent implementation of the ATLAS analyses Refs. [44, 45] with the use of the program package CheckMATE[33,34,35]. Below, we give a brief description of our implementation.
CheckMATE is an analysis tool to test BSM scenarios against LHC constraints. We implemented the searches of Ref. [44] and Ref. [45] using the AnalysisManager framework of CheckMATE. We validated our implementation against the cutflow tables for various signal regions provided by the ATLAS collaboration. For the validation, events with upto two additional partons were generated using MadGraph5_aMC@NLO [54], while showering and hadronization were performed with PYTHIA8 [55]. We used the PDF set NNPDF2.3LO [56] and CKKW-L prescription [57] for jet-parton matching following the ATLAS analyses. These events are then passed on to CheckMATE which uses Fastjet [58, 59] for jet reconstruction and Delphes [60] (which selects the ATLAS detector card) for fast detector simulation. After the preparation of final detector-level objects, CheckMATE performs a statistical evaluation for every signal region of each analysis. It compares the results of the simulation with the actual experimental data by computing the parameter r defined as,
where S denotes the expected number of signal events, \(\Delta S\) is the \(1~\sigma \) uncertainty on this number and \(S^{95}_{\mathrm{exp}}\) is the 95% confidence level upper limit on the signal cross-section quoted by the experimental collaboration. Thus, a parameter point is deemed to be excluded by the analysis provided the value of r exceeds 1.
Here, one should note that for the parameter region where compressed searches [51] are most sensitive, the difference between the “simplified model” and our scenario is rather mild. Therefore we impose these constraints directly onto our parameter space, keeping in mind that this provides a conservative exclusion limit. On the other hand, as mentioned earlier, the searches [48] described by Eq. (9) assume 100 % \(\text {BR}\) for the decay mode \({\tilde{\chi }}_{2}^0 \rightarrow h {\tilde{\chi }}_{1}^0\) (implying a predominantly wino-like \({\tilde{\chi }}_{2}^0\)). In practice, however, the \(\text {BR}\) for this decay mode is always smaller than 100% because of the presence of \({\tilde{\chi }}_{2}^0 \rightarrow Z {\tilde{\chi }}_{1}^0\) modeFootnote 2 (see also the discussion in [14, 15]). Thus, it is expected that this already sub-dominant limit will effectively be even substantially weaker for all practical SUSY scenarios. Therefore we do not apply this limit and accordingly did not implement this analysis independently in CheckMATE.
3.2 Constraints from measurements of \((g-2)_\mu \)
The experimental result for \(a_\mu := (g-2)_\mu /2\) is dominated by the measurements made at the Brookhaven National Laboratory (BNL) [61], resulting in a world average of [62]
where the first uncertainty is statistical and the second systematic. The SM prediction of \(a_\mu \) is given by [1]Footnote 3
Comparing this with the current experimental measurement in Eq. (14) results in a deviation of [1]
corresponding to a \(3.8\,\sigma \) discrepancy. This “current” result will be used below with a hard cut at \(2\,\sigma \) uncertainty.
Efforts to improve the experimental result at Fermilab by the “MUON G-2” collaboration [3] and at J-PARC [64] aim to reduce the experimental uncertainty by a factor of four compared to the BNL measurement. For the second step in our analysis we consider the upcoming Run 1 result from the Fermilab experiment. The Run 1 data is expected to have roughly the same experimental uncertainty as the current result in Eq. (14). We furthermore assume that the Run 1 data yields the same central value as the current result. Consequently, we anticipate that the combined uncertainty very roughly shrinks by \(1/\sqrt{2}\), yielding a future value of
corresponding to a \(5.4\,\sigma \) discrepancy. Thus, the combination of Run 1 data with the existing experimental \((g-2)_\mu \) data has the potential to establish the “discovery” of BSM phyics. This “anticipated future” result will be used below with a hard cut at \(2\,\sigma \) uncertainty.
Recently a new lattice calculation for the leading order hadronic vacuuum polarization (LO HVP) contribution to \(a_\mu ^{\mathrm{SM}}\) [65] has been reported. Their claim is that using their new lattice result, and in particular their strongly improved uncertainty estimate, the discrepancy of the SM prediction with the experimental result effectively disappears, in clear contrast to the evaluations based on experimental data [1, 2, 66]. Subsequently, in [67] it was argued that the uncertainty estimate of the LO HVP contribution obtained in [65] is far too optimistic, confirming earlier lattice based estimates. Furthermore, in Ref. [68] it was analyzed that the lattice evaluation of the LO HVP contribution creates a severe tension in the overall SM EW fit (see also [69, 70]). Consequently, while being aware of the theoretical developments of the LO HVP contributions, we stick to the central value of the deviation of \(a_\mu \) as given in Eq. (16) (in agreement with [63]). On the other hand, we are also aware that our conclusions would change substantially if the result presented in [65] turned out to be correct.
In MSSM the main contribution to \((g-2)_\mu \) at the one-loop level comes from diagrams involving \({\tilde{\chi }}_{1}^\pm -{\tilde{\nu }}\) and \({\tilde{\chi }}_{1}^0-{\tilde{\mu }}\) loops. The contributions are approximated as [71,72,73]
where the loop functions f are as given in Ref. [73]. In our analysis MSSM contribution to \((g-2)_\mu \) at two loop order is calculated using GM2Calc [74], implementing two-loop corrections from [75,76,77] (see also [78, 79]).
3.3 Dark matter relic density constraints
The mean density of CDM in the Universe is tightly constrained by Planck measurements of the cosmic microwave background and other observations [4]:
In an R-parity conserving scenario of MSSM, the lightest supersymmetric particle (LSP) becomes a candidate for DM. Depending on the hierarchy among the parameters \(M_1, M_2\) and \(\mu \) the LSP can be a bino-, wino- or higgsino-like state or an admixture of them. It is well-understood that with the current bounds on slepton masses from the LHC, a predominantly bino-like LSP is unable to achieve correct amount of relic density in the absence of some kind of coannihilation mechanism [12, 13]. A higgsino (wino) -like LSP, on the other hand is underabundant upto the mass of \(\sim \) 1 \(\,\, \mathrm {TeV}\) (3 \(\,\, \mathrm {TeV}\)) [80,81,82,83,84]. Thus, in the absence of sfermion-coannihilation, a well-tempered admixture of higgsino-bino or higgsino-wino states can give rise to the whole relic density of the universe single-handedly [85]. We assume here that the dominant source of the cold DM is the LSP, the lightest neutralino, \({\tilde{\chi }}_{1}^0\), so that \(\Omega _{\chi } h^{2}\simeq \Omega _{\mathrm{CDM}} h^2\). For the calculation of the DM relic density we use MicrOMEGAs [86,87,88,89].
3.4 Direct detection constraints of Dark matter
We evaluate the constraint on the spin-independent DM scattering cross-section \(\sigma _p^{\mathrm{SI}}\) from XENON1T [7] experiment, evaluating the theoretical prediction for \(\sigma _p^{\mathrm{SI}}\) using MicrOMEGAs [86,87,88,89]. While a combination with other DD experiments would yield slightly stronger limits, this would have no relevant impact on our results, as will be discussed below.
The leading contribution to \(\sigma _p^{\mathrm{SI}}\) in MSSM comes from t-channel Higgs exchange and s-channel squark exchange diagrams. Since, in our analysis the squarks and non-SM-like Higgses are taken to be significantly heavy, the contribution from the lightest CP-even Higgs exchange will be the dominant one. The \(h-{\tilde{\chi }}_{1}^0-{\tilde{\chi }}_{1}^0\) coupling arises as a result of mixing of the bino/wino and higgsino states [90]. Thus, in the parameter region \(\mu \simeq M_1, M_2\), the coupling can become significantly large. Moreover, since the coupling is \(\sim 1/m_{{\tilde{\chi }}_{1}^0}\), a smaller \(\sigma _p^{\mathrm{SI}}\) is expected for larger values of \(m_{{\tilde{\chi }}_{1}^0}\).
The scenario of \({\tilde{\chi }}_{1}^\pm /{\tilde{\chi }}_{2}^0\)-coannihilation analyzed in our work can arise from a mixed bino-wino or a bino-higgsino type of LSP. A bino-dominated LSP, on the other hand is expected to undergo \({\tilde{l}}^{\pm }\)-coannihilation to achieve the right relic density. Because of the tiny coupling of a bino with the Higgs, a predominantly-bino or a bino-wino mixed DM tend to have rather small \(\sigma _p^{\mathrm{SI}}\), often going below the neutrino floor [91,92,93,94]. However, as the higgsino component in the LSP increases, its \(\sigma _p^{\mathrm{SI}}\) can become large, thus receiving stringent bounds from the direct detection experiments. However, we must note that even a bino-higgsino well-tempered LSP can evade the direct detection bounds in some fine-tuned regions of parameter space dubbed as the ’blind spots’, where the \({\tilde{\chi }}_{1}^0\)-\({\tilde{\chi }}_{1}^0\)-h coupling at tree level becomes exactly equal to zero [95,96,97], and the signal can go below the neutrino floor [91,92,93]. There are in principle, constraints on \(\sigma _p^{\mathrm{SD}}\) as well [98, 99]. However, these limits are in general weaker than the \(\sigma _p^{\mathrm{SI}}\) ones.
4 Parameter scan and analysis flow
4.1 Parameter scan
We scan the relevant MSSM parameter space to obtain lower and upper limits on the relevant neutralino, chargino and slepton masses. In order to achieve the correct DM relic density, see Sect. 3.3, by the lightest neutralino, \({\tilde{\chi }}_{1}^0\), some mechanism such as a specific co-annhihilation or pole annihilation has to be active in the early universe. At the same time \(m_{{\tilde{\chi }}_{1}^0}\) must not be too high, such that the EW sector can provide the contribution required to bring the theory prediction of \(a_\mu \) into agreement with the experimental measurement, see Sect. 3.2. The combination of these two requirements yields the following possibilities. (The cases present a certain choice of favored possibilities, upon which one can expand, as will briefly discussed in Sect. 7.)
-
(A) \({\tilde{{\varvec{\chi }}}}_{\mathbf{1}}^{\pm }\) -coannihilation region
In order to achieve \({\tilde{\chi }}_{1}^\pm \)-coannihilation \(m_{{\tilde{\chi }}_{1}^0} \sim m_{{\tilde{\chi }}_{1}^\pm }\) is required. This can be achieved by
-
1.
\(M_1 \lesssim M_2~(\ll \mu )\) (bino-like LSP, or mixed bino-wino LSP)
-
2.
\(M_1 \lesssim \mu ~(\ll M_2)\) (bino-like LSP, or mixed bino-higgsino LSP)
-
3.
\(M_2 < M_1, \mu \) (wino-like LSP)
-
4.
\(\mu < M_1, M_2\) (higgsino-like LSP)
It is known [80,81,82,83,84] that a wino-like (higgsino-like) LSP fulfilling the relic density constraint, Eq. (20), results in \(m_{{\tilde{\chi }}_{1}^0} \sim 2.9 (1.1) \,\, \mathrm {TeV}\), which yields a SUSY spectrum too heavy to fulfil the \((g-2)_\mu \) constraint. On the other hand, the possibility of mixed bino-higgsino LSP is strongly constrained by the DD experiments, as discussed in Sect. 3.4. Consequently, we are left with the bino or mixed bino-wino like LSP. We choose the parameters according to,
$$\begin{aligned}&100 \,\, \mathrm {GeV}\le M_1 \le 1 \,\, \mathrm {TeV}, \quad M_1 \le M_2 \le 1.1 M_1, \nonumber \\&\quad 1.1 M_1 \le \mu \le 10 M_1, \; \quad 5 \le \tan \beta \le 60, \; \nonumber \\&\quad 100 \,\, \mathrm {GeV}\le m_{{\tilde{l}}_L}\le 1 \,\, \mathrm {TeV}, \; \quad m_{{\tilde{l}}_R}= m_{{\tilde{l}}_L}~. \end{aligned}$$(21)Here we choose one soft SUSY-breaking parameter for all sleptons together. While this choice should not have a relevant effect in the \({\tilde{\chi }}_{1}^\pm \)-coannihilation case, this have an impact in the next case. In our scans we will see that the chosen lower and upper limits are not reached by the points that meet all the experimental constraints. This ensures that the chosen intervals indeed cover all the relevant parameter space.
-
1.
-
\({\tilde{{{\varvec{l}}}}}^{\pm }\) -coannihilation region
Another well-known mechanism to bring the relic density of the \({\tilde{\chi }}_{1}^0\) into agreement with the experimental data is slepton coannihilation. As above we choose only one soft SUSY-breaking parameter for all slepton generations. This links automatically, stau-coannihilation and \(a_\mu \), which in principle are unrelated, see, e.g., [43, 100]. However, to keep the number of free parameters at a manageable level, we keep this restriction in our analysis and leave the case with different possible masses for different generations for future work. On the other hand, we cover the two distinct cases that either the SU(2) doublet sleptons, or the singlet sleptons are close in mass to the LSP.
- (B):
-
Case-L: SU(2) doublet
$$\begin{aligned}&100 \,\, \mathrm {GeV}\le M_1 \le 1 \,\, \mathrm {TeV}\;, \quad M_1 \le M_2 \le 10 M_1, \nonumber \\&\quad 1.1 M_1 \le \mu \le 10 M_1, \; \quad 5 \le \tan \beta \le 60, \; \nonumber \\&\quad M_1 \,\, \mathrm {GeV}\le m_{{\tilde{l}}_L}\le 1.2 M_1, \quad M_1 \le m_{{\tilde{l}}_R}\le 10 M_1~. \end{aligned}$$(22) - (C):
-
Case-R: SU(2) singlet
$$\begin{aligned}&100 \,\, \mathrm {GeV}\le M_1 \le 1 \,\, \mathrm {TeV}, \quad M_1 \le M_2 \le 10 M_1 \;, \nonumber \\&\quad 1.1 M_1 \le \mu \le 10 M_1, \; \quad 5 \le \tan \beta \le 60, \; \nonumber \\&\quad M_1 \,\, \mathrm {GeV}\le m_{{\tilde{l}}_R}\le 1.2 M_1,\; \quad M_1 \le m_{{\tilde{l}}_L}\le 10 M_1~. \end{aligned}$$(23)
In all three scans we choose flat priors of the parameter space and generate \(\mathcal{O}(10^7)\) points.
In particular in the Case-L up to six sleptons can be close in mass, the three charged “left-handed” sleptons as well as their respective neutralinos. To give an idea of the still present mass splitting we show in Fig. 2 the mass difference between the light smuon and (left) the muon sneutrino, or (right) the light stau. In green we show the points fulfilling the \((g-2)_\mu \) constraint (Eq. (16)), in dark blue the points that additionally give the correct DM relic density. The SU(2) relation enforces that the sneutrino is slightly lighter than the light smuon, with a mass difference ranging from \(\sim 25 \,\, \mathrm {GeV}\) for light smuons to about \(\sim 5 \,\, \mathrm {GeV}\) for heavy smuons. The non-zero splitting in the scalar tau sector, for equal soft SUSY-breaking parameters, makes the stau somewhat lighter than the smuon. Here the mass difference can go up to \(\sim 50 \,\, \mathrm {GeV}\). Consequently, depending on the parameter point, the NLSP can either be a sneutrino (the mass differences between the three generations are negligible) or the light scalar tau. For Case-R (not shown), taking also the DD limits into account, the “left-handed” sleptons being heavy, \({\tilde{\tau }_{2}}\) remains as the NLSP.
The mass parameters of the colored sector have been set to high values, such that the resulting SUSY particle masses are outside the reach of the LHC, the light \({\mathcal{CP}}\)-even Higgs-boson is in agreement with the LHC measurements, where the concrete values are not relevant for our analysis. \(M_A\) has also been set to be above the TeV scale. Consequently, we do not include explicitly the possibility of A-pole annihilation, with \(M_A\sim 2 m_{{\tilde{\chi }}_{1}^0}\). As we will discuss below the combination of direct heavy Higgs-boson searches with the other experimental requirements constrain this possibility substantially (see, however, also Sect. 7). Similarly, we do not consider h- or Z-pole annihilation, as such a light neutralino sector likely overshoots the \((g-2)_\mu \) contribution (see, however, the discussion in Sects. 6.2 and 7).
It should be kept in mind that while our three scenarios are “designed” to yield a certain coannihilation mechanism, the scan over the EW parameters is quite extensive. This ensures in particular that no “possibilities” to generate the required contribution to \((g-2)_\mu \) are overlooked.
4.2 Analysis flow
The data sample is generated by scanning randomly over the input parameter range mentioned above, using a flat prior for all parameters. We use SuSpect [101] as spectrum and SLHA file generator. The points are required to satisfy the \({\tilde{\chi }}_{1}^\pm \) mass limit from LEP [102]. The SLHA output files from SuSpect are then passed as input to GM2Calc and MicrOMEGAs for the calculation of \((g-2)_\mu \) and the DM observables, respectively. The parameter points that satisfy the current \((g-2)_\mu \) constraint, Eq. (16), the DM relic density, Eq. (20), and the direct detection constraints are then taken to the final step to be checked against the latest LHC constraints implemented in CheckMATE, as described in Sect. 3.1.Footnote 4 The branching ratios of the relevant SUSY particles are computed using SDECAY [104] and given as input to CheckMATE.
5 Results
5.1 \(\tilde{{\varvec{\chi }}}_{\mathbf{1}}^{\pm }\)-coannihilation region
We start our discussion with \({\tilde{\chi }}_{1}^\pm \)-coannihilation, as discussed in Sect. 4.1. We follow the analysis flow as described in Sect. 4.2 and denote the points surviving certain constraints with different colors.
-
grey (round): all scan points.
-
green (round): all points that are in agreement with \((g-2)_\mu \), taking into account the current or anticipated future limits, see Eqs. (16) and (17), respectively.
-
blue (triangle): points that additionally give the correct relic density, see Eq. (20).
-
cyan (diamond): points that additionally pass the DD constraints, see Sect. 3.4.
-
red (star): points that additionally pass the LHC constraints, see Sect. 3.1.
In Fig. 3 we show our results in the \(m_{{\tilde{\chi }}_{1}^0}\)–\(m_{{\tilde{\chi }}_{1}^\pm }\) plane for the current (left) and future (right) \((g-2)_\mu \) constraint, see Eqs. (16) and (17), respectively. By definition of \({\tilde{\chi }}_{1}^\pm \)-coannihilation the points are clustered in the diagonal of the plane. Starting with the \((g-2)_\mu \) constraint (green points) one can observe a clear upper limits from \((g-2)_\mu \) of about \(700 \,\, \mathrm {GeV}\) for the current limits and about \(600 \,\, \mathrm {GeV}\) from the anticipated future accuracy. Applying the CDM constraints reduce the upper limit further to about \(600 \,\, \mathrm {GeV}\) and \(450 \,\, \mathrm {GeV}\), respectively. Applying the LHC constraints, corresponding to the “surviving” red points (stars), does not yield a further reduction from above, but cuts always (as anticipated) only points in the lower mass range, see the discussion below. The LHC constraint which is effective in this parameter plane is the one designed for compressed spectra as given in Eq. (11) and shown as a green line in Fig. 1a. Thus, the experimental data set an upper as well as a lower bound, yielding a clear search target for the upcoming LHC runs, and in particular for future \(e^+e^-\) colliders, as will be discussed in Sect. 6. In particular, this collider target gets (potentially) sharpened substantially by the improvement in the \((g-2)_\mu \) measurements.
The impact of the DD experiments is demonstrated in Fig. 4. We show the \(m_{{\tilde{\chi }}_{1}^0}\)-\(\sigma _p^{\mathrm{SI}}\) plane for current (left) and anticipated future limits (right) from \((g-2)_\mu \). The color coding of the points (from yellow to dark green) denotes \(\mu /M_1\), whereas in blue (red) we show the points fulfilling the relic density (and additionally the LHC) constraints. The black line indicates the current DD limits, here taken for sake of simplicity from Xenon1T [7], as discussed in Sect. 3.4. It can be seen that a slight downward shift of this limit, e.g. due to additional DD experimental limits from LUX [5] or PANDAX [6], would not change our results in a relevant way. The scanned parameter space extends from large \(\sigma _p^{\mathrm{SI}}\) values, given for the smallest scanned \(\mu /M_1\) values to the smallest ones, reached for the largest scanned \(\mu /M_1\), i.e. the \(\sigma _p^{\mathrm{SI}}\) constraints is particularly strong for small \(\mu /M_1\). One can also see that the relic density constraint is fulfilled in nearly the whole scanned parameter space, except for the largest \(\sigma _p^{\mathrm{SI}}\) values. Given both CDM constraints and the LHC constraints, shown in red, the smallest \(\mu /M_1\) value we find is 2 for the current and 2.3 for the anticipated future \((g-2)_\mu \) bound. This result depends mildly on the assumed \((g-2)_\mu \) constraint, as this cuts away the largest \(m_{{\tilde{\chi }}_{1}^0}\) values.
Scan results in the \(m_{{\tilde{\chi }}_{1}^0}\)-\(\sigma _p^{\mathrm{SI}}\) plane for current (left) and anticipated future limits (right) from \((g-2)_\mu \). The color coding of the points denotes \(\mu /M_1\) and the black line indicates the DD limits (see text). In blue (red) we show the points fulfilling the relic density (and additionally the LHC) constraints
The results of our parameter scan in the \(m_{{\tilde{\chi }}_{1}^0}\)-\(m_{{\tilde{l}}_{1}}\) plane in the \({\tilde{\chi }}_{1}^\pm \)-coannihilation case (current (left) and anticipated future limits (right) from \((g - 2)_\mu \)). The color coding is as in Fig. 3
The distribution of the lighter slepton mass (where it should be kept in mind that we have chosen the same masses for all three generations, see Sect. 2) is presented in the \(m_{{\tilde{\chi }}_{1}^0}\)-\(m_{{\tilde{l}}_{1}}\) plane in Fig. 5, with the same color coding as in Fig. 3. The \((g-2)_\mu \) constraint places important constraints in this mass plane, since both types of masses enter into the contributing SUSY diagrams, see Sect. 3.2. The constraint is satisfied in a triangular region with its tip around \((m_{{\tilde{\chi }}_{1}^0}, m_{{\tilde{l}}_{1}}) \sim (700 \,\, \mathrm {GeV}, 800 \,\, \mathrm {GeV})\) in the case of current \((g-2)_\mu \) constraints, and around \(\sim (600 \,\, \mathrm {GeV}, 700 \,\, \mathrm {GeV})\) in the case of the anticipated future limits, i.e. the impact of the anticipated improved limits is clearly visible as an upper limit. Since no specific other requirement is placed on the slepton sector in the \({\tilde{\chi }}_{1}^\pm \)-coannihilation case the slepton masses are distributed over the \((g-2)_\mu \) allowed region. This also holds when the DM constraints are taken in to account, as can be seen in the distribution of the blue and cyan points (triangle/diamond).
The LHC constraints cut out lower slepton masses, going up to \(m_{{\tilde{l}}_{1}} \lesssim 400 \,\, \mathrm {GeV}\), as well as part of the very low \(m_{{\tilde{\chi }}_{1}^0}\) points nearly independent of \(m_{{\tilde{l}}_{1}}\). Here the latter “cut” is due to the searches for compressed spectra in Eq. (11), shown as green line in Fig. 1a. The first “cut” is mostly a result of the searches described in Eq. (10). It can be compared to the “naive” bound as given by the magenta line in Fig. 1b, where this bound extended up to \(m_{{\tilde{l}}_{1}} \lesssim 700 \,\, \mathrm {GeV}\), a strong reduction is observed. The reason for this reduction can be understood as follows. The ATLAS exclusion contour [45] for the mode in Eq. (10) is derived under the assumption that \({\tilde{e}}_L, {\tilde{\mu }}_L\) and \({\tilde{e}}_R, {\tilde{\mu }}_R\) are all mass-degenerate and sufficiently light to contribute to the signal cross-section. However, the right-sleptons can be significantly heavier for large parts of our parameter scan, with a correspondingly reduced production cross-section as compared to the ATLAS analysis. Moreover, \({\tilde{e}}_L\) has significant \(\text {BR}({\tilde{e}}_L \rightarrow {\tilde{\chi }}_{1}^\pm \nu _e)\) and similarly for \({\tilde{\mu }}_L\). This also reduces the number of signal leptons. Thus, a combination of these two factors leads to a substantially weaker exclusion limit. To illustrate this point better, in Table 2 we show the mass spectra and the relevant \(\text {BR}\)s of two representative points taken from the parameter space of \({\tilde{\chi }}_{1}^\pm \)-coannihilation scenario.
This emphasizes the importance of recasting using CheckMATE, rather than the “naive” application. Overall we can place an upper limit on the light slepton mass of about \(\sim 850 \,\, \mathrm {GeV}\) and \(750 \,\, \mathrm {GeV}\) for the current and the anticipated future accurary of \((g-2)_\mu \), respectively. Since larger values of slepton masses are reached for lower values of \(m_{{\tilde{\chi }}_{1}^0}\), the impact of \((g-2)_\mu \) is relatively weaker than in the case of chargino/neutralino masses. The phenomenological implications of these limits will be discussed in Sect. 6.
The results of our parameter scan in the \(m_{{\tilde{\chi }}_{1}^0}\)-\(\tan \beta \) plane for the \({\tilde{\chi }}_{1}^\pm \)-coannihilation scenario (current (left) and anticipated future limits (right) from \((g - 2)_\mu \)). The color coding is as in Fig. 3. The black line indicates the current exclusion bounds for heavy MSSM Higgs bosons at the LHC (see text)
The results of our parameter scan in the \(m_{\tilde{\mu }_{1}}-m_{{\tilde{\chi }}_{1}^0}\) plane for the \({\tilde{l}}^{\pm }\)-coannihilation Case-L (current (left) and anticipated future limits (right) from \((g - 2)_\mu \)). The color coding as in Fig. 3
We finish our analysis of the \({\tilde{\chi }}_{1}^\pm \)-coannihilation case with the \(m_{{\tilde{\chi }}_{1}^0}\)-\(\tan \beta \) plane presented in Fig. 6 with the same color coding as in Fig. 3. The \((g-2)_\mu \) constraint is fulfilled in a triangular region with largest neutralino masses allowed for the largest \(\tan \beta \) values (where we stopped our scan at \(\tan \beta = 60\)), following the analytic dependence of the \((g-2)_\mu \) contributions in Sect. 3.2, \(a_\mu \propto \tan \beta /m_{\mathrm{EW}}^2\) (where we denote with \(m_{\mathrm{EW}}\) an overall EW mass scale. In agreement with the previous plots, the largest values for the lightest neutralino masses are \(\sim 600 \,\, \mathrm {GeV}\) \((\sim 450 \,\, \mathrm {GeV})\) for the current (anticipated future) \((g-2)_\mu \) constraint. The points allowed by the DM constraints (blue/cyan) are distributed all over the allowed region. The LHC constraints cut out points at low \(m_{{\tilde{\chi }}_{1}^0}\), but nearly independent on \(\tan \beta \).
The results of our parameter scan in the \(\sigma _p^{\mathrm{SI}}-m_{{\tilde{\chi }}_{1}^0}\) plane for the \({\tilde{l}}^{\pm }\)-coannihilation Case-L (current (left) and anticipated future limits (right) from \((g - 2)_\mu \)). The color coding as in Fig. 4
The results of our parameter scan in the \(m_{{\tilde{\chi }}_{1}^\pm }-m_{{\tilde{\chi }}_{1}^0}\) plane for the \({\tilde{l}}^{\pm }\)-coannihilation Case-L (current (left) and anticipated future limits (right) from \((g - 2)_\mu \)). The color coding as in Fig. 7
In Fig. 6 we also show as black lines the current bound from LHC searches for heavy neutral Higgs bosons [105] in the channel \(pp \rightarrow H/A \rightarrow \tau \tau \) in the \(M_h^{125}({\tilde{\chi }})\) benchmark scenario (based on the search data published in Refs. [106, 107] using \(36\, \text {fb}^{-1}\).).Footnote 5 In this scenario light charginos and neutralinos are present, suppressing the \(\tau \tau \) decay mode and thus yielding relatively weak limits in the \(M_A\)-\(\tan \beta \) plane (see Fig. 5 in [105]). The black lines correspond to \(m_{{\tilde{\chi }}_{1}^0} = M_A/2\), i.e. roughly to the requirement for A-pole annihilation, where points above the black lines are experimentally excluded. There are a few points passing the current \((g-2)_\mu \) constraint below the black A-pole line, reaching up to \(m_{{\tilde{\chi }}_{1}^0} \sim 280 \,\, \mathrm {GeV}\), for which the A-pole annihilation could provide the correct DM relic density. It can be expected that with the improved limits as given in [108] this possibility is further restricted. Taking into account the anticipated future \((g-2)_\mu \) accuracy (keeping in mind the hypothetical future central value is the same as the current one) also cuts away most of the points below the black A-pole line. The combination of these effects makes the A-pole annihilation in this scenario marginal.
5.2 \({\tilde{{{\varvec{l}}}}}^{\pm }\)-coannihilation region: Case-L
We now turn to the case of \({\tilde{l}}^{\pm }\)-coannihilation. As discussed in in Sect. 4.1 we distinguish two cases, depending which of the two slepton soft SUSY-breaking parameters is set to be close to \(m_{{\tilde{\chi }}_{1}^0}\). In Case-L we chose \(m_{{\tilde{l}}_{L}} \sim M_1\), i.e. the left-handed charged sleptons as well as the sneutrinos are close in mass to the LSP. We find that all six sleptons are close in mass and differ by less than \(\sim 50 \,\, \mathrm {GeV}\), see Fig. 2.
In Fig. 7 we show the results of our scan in the \(m_{\tilde{\mu }_{1}} -m_{{\tilde{\chi }}_{1}^0}\) plane. The color coding of the points is the same as in Fig. 3, see the description in the beginning of Sect. 5.1. The green points in the left plot satisfy the current \((g-2)_\mu \) constraints of Eq. (16) whereas in the right plot these points correspond to the anticipated future experimental bound of \((g-2)_\mu \) as given in Eq. (17). By definition of the scenario, the points are located along the diagonal of the plane. The present constraint from \((g-2)_\mu \) puts an upper bound of \(\sim 650 \,\, \mathrm {GeV}\) on the masses. With the projected sensitivity the upper limit is slightly reduced to \(\sim 550 \,\, \mathrm {GeV}\). Including the DM and LHC constraints, these bounds are reduced to \(\sim 550 \,\, \mathrm {GeV}\) and \(\sim 500 \,\, \mathrm {GeV}\) for the current and anticipated future \((g-2)_\mu \) accuracy, respectively. As in the case of \({\tilde{\chi }}_{1}^\pm \)-coannihilation the LHC constraints cut away only low mass points. The corresponding implications for the searches at future colliders are discussed in Sect. 6.
The impact of the DD experiments in the Case-L is demonstrated in Fig. 8. We show the \(m_{{\tilde{\chi }}_{1}^0}\)-\(\sigma _p^{\mathrm{SI}}\) plane for current (left) and anticipated future limits (right) from \((g-2)_\mu \). The color coding of the points is as in Fig. 4. As above, the black line indicates the current DD limits [7]. The general features are as in the \({\tilde{\chi }}_{1}^\pm \)-coannihilation scenario: the scanned parameter space extends from large \(\sigma _p^{\mathrm{SI}}\) values, given for the smallest scanned \(\mu /M_1\) values to the smallest ones, reached for the largest scanned \(\mu /M_1\). One can also see that the relic density constraint is fulfilled in nearly the whole scanned parameter space but spreading mostly towards higher \(\mu /M_1\) values. Given both CDM constraints and the LHC constraints, the smallest \(\mu /M_1\) value we find is 2.46 for both the current and the anticipated future \((g-2)_\mu \) bound.
In Fig. 9 we show the results in the \(m_{{\tilde{\chi }}_{1}^0}\)-\(m_{{\tilde{\chi }}_{1}^\pm }\) plane with the same color coding as in Fig. 7. The \((g-2)_\mu \) limits on \(m_{{\tilde{\chi }}_{1}^0}\) become slightly stronger for larger chargino masses, as expected from Eq. (19), and upper limits on the chargino mass are set at \(\sim 3 \,\, \mathrm {TeV}\) (\(\sim 2.5 \,\, \mathrm {TeV}\)) for the current (anticipated future) precision in \(a_\mu \). The LHC limits cut away a lower wedge going up to \(m_{{\tilde{\chi }}_{1}^\pm } \lesssim 600 \,\, \mathrm {GeV}\), driven by the bound in Eq. (5), shown as the red dashed line in Fig. 1a. As in the \({\tilde{\chi }}_{1}^\pm \)-coannihilation case, also here the upper limit on \(m_{{\tilde{\chi }}_{1}^\pm }\) is strongly reduced w.r.t. the “naive” application, which goes up to \(m_{{\tilde{\chi }}_{1}^\pm } \lesssim 1100 \,\, \mathrm {GeV}\) for negligible \(m_{{\tilde{\chi }}_{1}^0}\). The reason for the weaker limit can be attributed to two factors. First, the significant branching ratios of \(\text {BR}({\tilde{\chi }}_{1}^\pm \rightarrow {\tilde{\tau }_{1}} \nu _\tau )\) and \(\text {BR}({\tilde{\chi }}_{2}^0 \rightarrow {\tilde{\tau }_{1}} \tau )\) respectively, which are considered to be absent in the ATLAS analysis. Second, the notably large branching ratio of \({\tilde{\chi }}_{2}^0\) to the invisible modes \({\tilde{\chi }}_{2}^0 \rightarrow {\tilde{\nu }}\nu \). Table 3 gives an idea of the relevant \(\text {BR}\)s of two sample points taken from the parameter space of Case-L, with their mass spectra given in the same table. This again emphasizes the importance of the recasting of the LHC searches that we have applied.
The results of our parameter scan in the \(\tan \beta -m_{{\tilde{\chi }}_{1}^0}\) plane for the \({\tilde{l}}^{\pm }\)-coannihilation Case-L (current (left) and anticipated future limits (right) from \((g - 2)_\mu \)) . The color coding is as in Fig. 7
The results for the \({\tilde{l}}^{\pm }\)-coannihilation Case-L in the \(m_{{\tilde{\chi }}_{1}^0}\)-\(\tan \beta \) plane are presented in Fig. 10. The overall picture is similar to the \({\tilde{\chi }}_{1}^\pm \)-coannhiliation case shown above in Fig. 6. Larger LSP masses are allowed for larger \(\tan \beta \) values. On the other hand the combination of small \(m_{{\tilde{\chi }}_{1}^0}\) and large \(\tan \beta \) leads to a too large contribution to \(a_\mu ^{\mathrm{SUSY}}\) and is thus excluded. As in Fig. 6 we also show the limits from H/A searches at the LHC, where we set (as above) \(m_{{\tilde{\chi }}_{1}^0} = M_A/2\), i.e. roughly to the requirement for A-pole annihilation, where points above the black lines are experimentally excluded. In this case for the current \((g-2)_\mu \) limit substantially more points passing the \((g-2)_\mu \) constraint “survive” below the black line, i.e. they are potential candidates for A-pole annihilation. The masses reach up to \(\sim 320 \,\, \mathrm {GeV}\). As in the case of \({\tilde{\chi }}_{1}^\pm \)-coannihilation, see Fig. 6, these points are reduced in the case of the anticipated future \((g-2)_\mu \) accuracy with an upper limit of \(\sim 260 \,\, \mathrm {GeV}\). Together with the already stronger bounds on \(H/A \rightarrow \tau \tau \) [108] this does not fully exclude A-pole annihilation, but leaves it as a rather remote possibility with a clear upper bound on \(m_{{\tilde{\chi }}_{1}^0}\) (see the discussion in Sect. 6.2).
The results of our parameter scan in the \(m_{{\tilde{\chi }}_{1}^0}\)-\(m_{\tilde{\mu }_{2}}\) plane for the \({\tilde{l}}^{\pm }\)-coannihilation Case-R. The color coding as in Fig. 3
The results of our parameter scan in the \(m_{{\tilde{\chi }}_{1}^0}\)-\(m_{\tilde{\mu }_{1}}\) plane for the \({\tilde{l}}^{\pm }\)-coannihilation Case-R (current (left) and anticipated future limits (right) from \((g - 2)_\mu \)). The color coding as in Fig. 11
5.3 \({\tilde{{{\varvec{l}}}}}^{\pm }\)-coannihilation region: Case-R
We now turn to our third scenario, \({\tilde{l}}^{\pm }\)-coannihilation Case-R, where in the scan we require the “right-handed” sleptons to be close in mass with the LSP. It should be kept in mind that in our notation we do not mass-order the sleptons: for negligible mixing as it is given for selectrons and smuons the “left-handed” (“right-handed”) slepton corresponds to \({\tilde{l}}_1\) (\({\tilde{l}}_2\)). As it will be seen below, in this scenario all relevant mass scales are required to be relatively light by the \((g-2)_\mu \) constraint.
We start in Fig. 11 with the \(m_{{\tilde{\chi }}_{1}^0}\)-\(m_{\tilde{\mu }_{2}}\) plane with the same color coding as in Fig. 3. By definition of the scenario the points are concentrated on the diagonal. The current (future) \((g-2)_\mu \) bound yields upper limits on the LSP of \(\sim 700\, (600) \,\, \mathrm {GeV}\), as well as an upper limit on \(m_{\tilde{\mu }_{2}}\) (which is close in mass to the \({\tilde{e}}_{2}\) and \({\tilde{\tau }_{2}}\)) of \(\sim 800\, (700) \,\, \mathrm {GeV}\). Including the CDM and LHC constraints, these limits reduce to \(\sim 520\,(400) \,\, \mathrm {GeV}\) for the LSP for the current (future) \((g-2)_\mu \) bounds, and correspondingly to \(\sim 600\,(430) \,\, \mathrm {GeV}\) for \(m_{\tilde{\mu }_{2}}\), and \(\sim 530\,(410) \,\, \mathrm {GeV}\) for \(m_{\tilde{\tau }_{2}}\). The LHC constraints cut out some, but not all lower-mass points.
The distribution of the heavier slepton is displayed in the \(m_{{\tilde{\chi }}_{1}^0}\)-\(m_{\tilde{\mu }_{1}}\) plane in Fig. 12. Although the “left-handed” sleptons are allowed to be much heavier, the \((g-2)_\mu \) constraint imposes an upper limit of \(\sim 950~(800) \,\, \mathrm {GeV}\) in the case for the current (future) \((g-2)_\mu \) precision. This can be understood from the SUSY contributions to \(a_\mu \). If the “left-handed” slepton is heavy this suppresses both contributions, the chargino-sneutrino loop as given in Eq. (18), as well as the neutralino-slepton loop as given in Eq. (19). Consequently, in particular the “left-handed” slepton soft SUSY-breaking parameter must not be too large to give a relevant contribution to \(a_\mu ^{\mathrm{SUSY}}\). Valid parameter point with maximum \(m_{\tilde{\mu }_{1}}\) \(\sim 750 \,\, \mathrm {GeV}\) for both the current and future \((g-2)_\mu \) precision are obtained, even after the inclusion of DM and LHC constraints. This offers in principle very optimistic future collider prospects, as will be discussed in Sect. 6. In particular the LHC limits cut away lower mass points and set a lower limit of \(\sim 300 \,\, \mathrm {GeV}\) for the heavier sleptons in the Case-R. This is predominantly due to the LHC limits from slepton pair production following the decay pattern of Eq. (10) and shown as the magenta region in Fig. 1b. Unlike Case-L, the lighter masses for both the “left-” and “right-handed” sleptons contribute to larger production cross-section and lead to the exclusion. Additionally, the chargino, being mostly wino-like, prefers to decay via light “left-handed” sleptons in the kinematically allowed region. These points are further restricted by LHC searches for chargino production with a subsequent decay via sleptons as in Eqs. (5)–(6). These limits are depicted as red and magenta region in Fig. 1a. The masses and decay patterns of two sample points from the parameter space of Case-R scenario is given in Table 4.
The impact of the DD experiments in the Case-R is demonstrated in Fig. 13. We show the \(m_{{\tilde{\chi }}_{1}^0}\)-\(\sigma _p^{\mathrm{SI}}\) plane for current (left) and anticipated future limits (right) from \((g-2)_\mu \). The color coding of the points is as in Fig. 4. As above, the black line indicates the current DD limits from XENON1T [7]. The general features are similar to the \({\tilde{l}}^{\pm }\)-coannihilation Case-L scenario: the scanned parameter space extends from large \(\sigma _p^{\mathrm{SI}}\) values, given for the smallest scanned \(\mu /M_1\) values to the smallest ones, reached for the largest scanned \(\mu /M_1\). However, there is one important change w.r.t. Case-L: the \((g-2)_\mu \) bound tends to drive \(\mu \) to lower values, whereas larger values are preferred by the DD constraint. This “tension” results in more intricate relations among the parameters to be fulfilled in order to meet the various constraints at once. Although, one can also see that the relic density constraint is fulfilled in nearly the whole scanned parameter space. Given both CDM constraints and the LHC constraints, the smallest \(\mu /M_1\) value we find is smaller than in the Case-L: 1.7 and 2.0 for the current and the anticipated future \((g-2)_\mu \) bound.
The results of our parameter scan in the \(m_{{\tilde{\chi }}_{1}^0}\)-\(\sigma _p^{\mathrm{SI}}\) plane for the \({\tilde{l}}^{\pm }\)-coannihilation Case-R (current (left) and anticipated future limits (right) from \((g - 2)_\mu \)). The color coding as in Fig. 4
The results of our parameter scan in the \(m_{{\tilde{\chi }}_{1}^\pm }-m_{{\tilde{\chi }}_{1}^0}\) plane for the \({\tilde{l}}^{\pm }\)-coannihilation Case-R (current (left) and anticipated future limits (right) from \((g - 2)_\mu \)). The color coding as in Fig. 11
In Fig. 14 we show the results in the \(m_{{\tilde{\chi }}_{1}^0}\)-\(m_{{\tilde{\chi }}_{1}^\pm }\) plane with the same color coding as in Fig. 11. As in the Case-L the \((g-2)_\mu \) limits on \(m_{{\tilde{\chi }}_{1}^0}\) become slightly stronger for larger chargino masses, as expected from Eq. (19). The upper limits on the chargino mass, however, are substantially stronger as in the Case-L. They are reached at \(\sim 1.6 \,\, \mathrm {TeV}\) for the current and \(\sim 1.3 \,\, \mathrm {TeV}\) for the anticipated future precision in \(a_\mu \). On the other hand there are points with very low \(m_{{\tilde{\chi }}_{1}^\pm }\), which are not affected by the LHC searches, which can be understood as follows. The LHC-excluded points span in principle the entire parameter space allowed by \((g-2)_\mu \) constraint with the bounds coming from the searches discussed in the context of Fig. 12. The points with lowest \(m_{{\tilde{\chi }}_{1}^\pm }\) values, which are not cut away by the LHC searches correspond to the mass hierarchy \(m_{\tilde{e}_{1}}> m_{{\tilde{\chi }}_{1}^\pm }, m_{{\tilde{\chi }}_{2}^0}> m_{\tilde{e}_{2}} > m_{\tilde{\tau }_{2}}\), with \(m_{\tilde{e}_{1}}\) being relatively large. Such a configuration implies large \(\text {BR}({\tilde{\chi }}_{1}^\pm \rightarrow {\tilde{\tau }_{2}} \nu _\tau )\) and \(\text {BR}({\tilde{\chi }}_{2}^0 \rightarrow {\tilde{\tau }_{2}} \tau )\), leading to a substantially weaker LHC bounds, as discussed above. For these “allowed” points with low \(m_{{\tilde{\chi }}_{1}^\pm }\) also \({\tilde{\chi }}_{1}^\pm \)-coannihilation contributes relevantly to the CDM relic density.
The results of our parameter scan in the \(m_{{\tilde{\chi }}_{1}^0}\)-\(\tan \beta \) plane for the \({\tilde{l}}^{\pm }\)-coannihilation Case-R (current (left) and anticipated future limits (right) from \((g - 2)_\mu \)). The color coding is as in Fig. 11
We finish our analysis of the \({\tilde{l}}^{\pm }\)-coannihilation Case-R with the results in the \(m_{{\tilde{\chi }}_{1}^0}\)-\(\tan \beta \) plane, presented in Fig. 15. The overall picture is similar to the previous cases shown above in Figs. 6, 10. Larger LSP masses are allowed for larger \(\tan \beta \) values. On the other hand the combination of small \(m_{{\tilde{\chi }}_{1}^0}\) and very large \(\tan \beta \) values, \(\tan \beta \gtrsim 40\) leads to stau masses below the LSP mass, which we exclude for the CDM constraints. The LHC searches mainly affect parameter points with \(\tan \beta \lesssim 20\). Larger \(\tan \beta \) values induce a larger mixing in the third slepton generation, enhancing the probability for charginos to decay via staus and thus evading the LHC constraints, see the discussion in Sect. 3.1. As in Fig. 10 we also show the limits from H/A searches at the LHC, where we set (as above) \(m_{{\tilde{\chi }}_{1}^0} = M_A/2\), i.e. roughly to the requirement for A-pole annihilation, where points above the black lines are experimentally excluded. Comparing Case-R and Case-L, here for the current \((g-2)_\mu \) limit substantially less points are passing the current \((g-2)_\mu \) constraint below the black line, i.e. are potential candidates for A-pole annihilation. The masses reach only up to \(\sim 200 \,\, \mathrm {GeV}\). As in the two previous cases, see Figs. 6, 10, these points are reduced in the case of the anticipated future \((g-2)_\mu \) accuracy with an upper limit of \(\sim 180 \,\, \mathrm {GeV}\). Together with the already stronger bounds on \(H/A \rightarrow \tau \tau \) [108] this leaves A-pole annihilation as a quite remote possibility with a strict upper bound on \(m_{{\tilde{\chi }}_{1}^0}\) (see the discussion in Sect. 6.2).
5.4 Lowest and highest mass points
In this section we present some sample spectra for the three cases discussed in the previous subsections. For each case, \({\tilde{\chi }}_{1}^\pm \)-coannihilation, \({\tilde{l}}^{\pm }\)-coannihilation Case-L and Case-R, we present three parameter points that are in agreement with all constraints (red points): the lowest LSP mass, the highest LSP with current \((g-2)_\mu \) constraints, as well as the highest LSP mass with the anticipated future \((g-2)_\mu \) constraint. They will be labeled as “C1, C2, C3”, “L1, L2, L3”, “R1, R2, R3” for \({\tilde{\chi }}_{1}^\pm \)-coannihilation, \({\tilde{l}}^{\pm }\)-coannihilation Case-L and Case-R,respectively. While the points are obtained from “random sampling”, nevertheless they give an idea of the mass spectra realized in the various scenarios. In particular, the highest mass points give an clear indication on the upper limits of the NLSP mass.
In Table 5 we show the 3 parameter points (“C1, C2, C3”) from \({\tilde{\chi }}_{1}^\pm \)-coannihilation scenario, which are defined by the six scan parameters: \(M_1\), \(M_2\), \(\mu \), \(\tan \beta \) and the two slepton mass parameters, \(m_{{\tilde{l}}_{L}}\) and \(m_{{\tilde{l}}_{R}}\) (corresponding roughly to \(m_{{\tilde{e}}_1, {\tilde{\mu }}_1}\) and \(m_{{\tilde{e}}_2, {\tilde{\mu }}_2}\), respectively). Together with the masses and relevant \(\text {BR}\)s we also show the values of the DM observables and \(a_\mu ^{\mathrm{SUSY}}\). Since \({\tilde{\tau }}\) is the NLSP in these three cases, the contribution from \({\tilde{\tau }}\)-coannihilation together with \({\tilde{\chi }}_{1}^\pm \)-coannihilation brings the relic density to the ballpark value. For all of the three points, the decays of \({\tilde{\chi }}_{1}^\pm \) and \({\tilde{\chi }}_{2}^0\) to first two generations of sleptons are not kinematically accessible. Therefore they decay with 100% BR to third generation charged sleptons and sneutrinos. This makes them effectively invisible to the LHC searches looking for electrons and muons in the signal. LHC analyses designed to specifically look for \(\tau \)-rich final states can prove beneficial to constrain these points, which are much less powerful, as discussed above.
In Table 6 we show three parameter points (“L1, L2, L3”) taken from \({\tilde{l}}^{\pm }\)-coannihilation scenario Case-L, defined in the same way as in the \({\tilde{\chi }}_{1}^\pm \)-coannihilation case. For the point L1, \({\tilde{\chi }}_{1}^\pm \) and \({\tilde{\chi }}_{2}^0\) are higgsino-dominated with a significant wino component, they are almost mass-degenerate with \({\tilde{\chi }}_{3}^0\). For L2 and L3, on the other hand, \({\tilde{\chi }}_{1}^\pm \) and \({\tilde{\chi }}_{2}^0\) are wino-like. For this reason, L1 has a significant \(\text {BR}({\tilde{\chi }}_{2}^0 \rightarrow {\tilde{\chi }}_{1}^0 h)\) which is absent for L2 and L3. The large values of \(m_{\tilde{\mu }_{2}}\) for the three points implies that the dominant one-loop contribution to \((g-2)_\mu \) comes from the diagram involving \({\tilde{\chi }}_{1}^\pm -{\tilde{\nu }}\) in the loop.
The masses, \(\text {BR}\)s and values of the \((g-2)_\mu \) and DM observables of the three parameter points for the Case-R (“R1, R2, R3”) are shown in Table 7. Compared to the points C1 and L1 of the previous two cases, the point R1 needs a larger value of \(\tan \beta \) to satisfy \((g-2)_\mu \) constraint. The mass splitting between \({\tilde{\mu }}_{1}\) and \({\tilde{\mu }}_{2}\) is also seen to be smaller than that of Case-L, for reasons discussed in Sect. 5.3. The wino-dominated \({\tilde{\chi }}_{1}^\pm \) and \({\tilde{\chi }}_{2}^0\) preferably decay via \({\tilde{e}}_{1}/{\tilde{\mu }}_{1}\), which, however, are kinematically forbidden in these cases. The decays via \({\tilde{e}}_{2}/{\tilde{\mu }}_{2}\), on the other hand, are suppressed because of the tiny Yukawa couplings of the first two generations. Therefore, they decay entirely to final states involving third generation sleptons, making them harder to detect.
6 Prospects for future colliders
In this section we discuss the prospects of the direct detection of the (relatively light) EW particles at the approved HL-LHC and at a hypothetical future \(e^+e^-\) collider such as ILC [36, 37] or CLIC [37,38,39,40].
6.1 HL-LHC prospects
The projected (left) 95% exclusion limit and (right) a 5\(\sigma \) discovery reach in the \(m_{{\tilde{\chi }}_{1}^0}\)-\(m_{{\tilde{\chi }}_{1}^\pm }\) plane at the HL-LHC. The color coding for various decay modes are as in Fig. 1
The prospects for BSM phenomenology at the HL-LHC have been summarized in [109] for a 14 TeV run with 3 \(\text {ab}^{-1}\) of integrated luminosity. For the direct production of chargino and neutralino through EW interaction, the projected 95% exclusion reach as well as a 5\(\sigma \) discovery reach have been presented. For the non-compressed scenario, the electroweak gaugino production via on-shell gauge boson decays has been analyzed following Eqs. (7a) and (8). The corresponding limits in the \(m_{{\tilde{\chi }}_{1}^0}\)-\(m_{{\tilde{\chi }}_{1}^\pm }\) plane is shown in Fig. 16 with cyan and blue shaded regions respectively. The color coding follows the same convention as in Fig. 1. The projected exclusion reach for the cyan region will go twice as high in the chargino mass range, covering values as high as 1 TeV for \(m_{{\tilde{\chi }}_{1}^0} \lesssim 500 \,\, \mathrm {GeV}\). However, the most significant improvement can be observed in the gaugino productions via on-shell W and Higgs decays as in Eq. (9), shown as yellow shaded area. On the other hand, the same search channel has a projected \(5\,\sigma \) reach up to \(m_{{\tilde{\chi }}_{1}^\pm } \lesssim 1 \,\, \mathrm {TeV}\) and \(m_{{\tilde{\chi }}_{1}^0} \lesssim 500 \,\, \mathrm {GeV}\). Therefore, this search channel with an on-shell Higgs decaying to \(b{\bar{b}}\) combined with the future \((g-2)_\mu \) accuracy and DM constraints can conclusively probe “almost” the entire allowed parameter region of \({\tilde{l}}^{\pm }\)-coannihilation Case-R scenario and a significant part of the same parameter space for Case-L scenario (see Figs. 9, 14) at the HL-LHC. We note that no update was provided in [109] for the most relevant search channels, the decay of charginos/neutralinos via intermediate sleptons with 3l and 2l final states, see Eqs. (5), (6). A clearer picture of the HL-LHC prospects for the physics case under investigation could be drawn with an experimental analysis of these channels.
Similarly, no prospects for the scalar electron or muon production at the HL-LHC have been reported yet. However, the analysis for compressed higgsino-like spectra may exclude \(m_{{\tilde{\chi }}_{2}^0} \sim m_{{\tilde{\chi }}_{1}^\pm } \sim 350 \,\, \mathrm {GeV}\) with mass gap as low as 2 GeV for \(m_{{\tilde{\chi }}_{1}^\pm }\) around 100 GeV following the decay pattern of Eq. (11). Hence, a substantial parameter region can be curbed for the \({\tilde{\chi }}_{1}^\pm \)-coannihilation case (see Fig. 3) in the absence of a signal in the compressed scenario analysis with soft leptons at the final state.
6.2 ILC/CLIC prospects
Direct production of EW particles at \(e^+e^-\) colliders clearly profits from a higher center-of-mass energy, \(\sqrt{s}\). Consequently, we focus here on the two proposals for linear \(e^+e^-\) colliders, ILC [36, 37] and CLIC [37,38,39,40], which can reach energies up to \(1 \,\, \mathrm {TeV}\), and \(3 \,\, \mathrm {TeV}\), respectively. We evaluate the cross-sections for the various SUSY pair production modes for the energies currently foreseen in the run plans of the two colliders. The anticipated energies and integrated luminosities are listed in Table 8. The cross-section predictions are based on tree-level results, obtained as in [110, 111], where it was shown that the full one-loop corrections can amount up to 10–20%.Footnote 6 We do not attempt any rigorous experimental analysis, but follow the idea that to a good approximation final states with the sum of the masses smaller than the center-of-mass energy can be detected [113,114,115]. We also note that in case of several EW SUSY particles in reach of an \(e^+e^-\) collider, large parts of the overall SUSY spectrum can be measured and fitted [116].
In the following we show the results for certain EW-SUSY production cross-sections for a fixed \(\sqrt{s}\) (according to Table 8). We do not show the production cross-sections for the mono-photon signal \(e^+e^- \rightarrow {\tilde{\chi }}_{1}^0{\tilde{\chi }}_{1}^0 (+\gamma )\) (where the ISR photon is required to detect the invisible final state). From the upper limits on \(m_{{\tilde{\chi }}_{1}^0}\) as obtained in Sect. 5 (about \(570 \,\, \mathrm {GeV}\) for \({\tilde{\chi }}_{1}^\pm \)-coannihilation, about \(540 \,\, \mathrm {GeV}\) for \({\tilde{l}}^{\pm }\)-coannihilation Case-L and about \(520 \,\, \mathrm {GeV}\) in Case-R, for the current \((g-2)_\mu \) constraint), it can be inferred that with \(\sqrt{s} = 1000 \,\, \mathrm {GeV}\) a considerable part of the spectrum can be covered. The reach becomes even stronger in the case of the future anticipated \((g-2)_\mu \) constraint, where the upper limits on \(m_{{\tilde{\chi }}_{1}^0}\) go down to \(\sim 430, 500, 410 \,\, \mathrm {GeV}\), respectively, covering effectively the full spectrum at a \(1000 \,\, \mathrm {GeV}\) collider.
cross-section predictions for \(e^+e^- \rightarrow {\tilde{\chi }}_{1}^\pm {\tilde{\chi }}_{1}^\mp \) (left) and \(e^+e^- \rightarrow {\tilde{\mu }}_{1}{\tilde{\mu }}_{1}\) (right) in the \({\tilde{\chi }}_{1}^\pm \)-coannihilation case at the ILC and CLIC as a function of the sum of the final state masses. Open (filled) circles indicate agreement with \((g-2)_\mu \) at the current (anticipated future) accuracy
We start the numerical investigations in Fig. 17 with the cross-section predictions for \(e^+e^- \rightarrow {\tilde{\chi }}_{1}^\pm {\tilde{\chi }}_{1}^\mp \) (left) and \(e^+e^- \rightarrow {\tilde{\mu }}_{1}{\tilde{\mu }}_{1}\) (right) in the \({\tilde{\chi }}_{1}^\pm \)-coannihilation case as a function of the sum of the final state masses. The different shades of green (violet) indicate the cross-sections at the various ILC (CLIC) energies. Open (filled) circles indicate agreement with \((g-2)_\mu \) at the current (anticipated future) accuracy. It can be observed that the lower-energy stages of the ILC and CLIC, \(\sqrt{s} \le 500 \,\, \mathrm {GeV}\), cover only a very small part of the predicted mass spectrum. (\(\sqrt{s} = 250 \,\, \mathrm {GeV}\) does not yield any accessible parameter point in our analysis.) Higher energies, on the other hand, as can be reached in principle at future \(e^+e^-\) colliders cover part or even the full predicted spectrum. This holds particularly for the CLIC energies for the parameter points assuming the current \((g-2)_\mu \) constraint. On the other hand, even the ILC1000 can cover the full predicted \(m_{{\tilde{\chi }}_{1}^\pm }\) spectrum in the case of the future anticipated \((g-2)_\mu \) constraint. All obtained cross-section predictions for the kinematically accessible parameter points are above \(10^{-2}\) pb for chargino production and above \(10^{-3}\) pb for smuon pair production. For each \(\text {ab}^{-1}\) of integrated luminosity this corresponds to 10,000 (1000) events for chargino (smuon) pair production, which should make these particles easily accessible, see Table 8, if they are in the kinematic reach of the collider.
Cross-section predictions for \(e^+e^- \rightarrow {\tilde{\chi }}_{1}^0{\tilde{\chi }}_{2}^0\) (left) and \(e^+e^- \rightarrow {\tilde{\mu }}_{1}{\tilde{\mu }}_{1}\) (right) in the \({\tilde{l}}^{\pm }\)-coannihilation Case-L at the ILC and CLIC as a function of the sum of the final state masses. Symbols are as in Fig. 17
The situation is similar, but somewhat less encouraging for \({\tilde{l}}^{\pm }\)-coannihilation Case-L, as presented in Fig. 18. The left (right) plot shows the cross-section predictions for \(e^+e^- \rightarrow {\tilde{\chi }}_{1}^0{\tilde{\chi }}_{2}^0\) and \(e^+e^- \rightarrow {\tilde{\mu }}_{1}{\tilde{\mu }}_{1}\) with the same symbol/color coding as in Fig. 17. Here highest CLIC energies are needed to cover the full predicted spectrum. On the other hand, the lighter sleptons are closer in mass to the LSP in this scenario. Consequently, even the ILC500 can cover a substantial part of the predicted \(m_{\tilde{\mu }_{1}}\) spectrum, and \(\sqrt{s} \lesssim 1000 \,\, \mathrm {GeV}\) is sufficient to cover all predicted mass values.
Cross-section predictions for \(e^+e^- \rightarrow {\tilde{\chi }}_{1}^0{\tilde{\chi }}_{2}^0\) (left) and \(e^+e^- \rightarrow {\tilde{\mu }}_{2}{\tilde{\mu }}_{2}\) (right) in the \({\tilde{l}}^{\pm }\)-coannihilation Case-R at the ILC and CLIC as a function of the sum of the final state masses. Symbols are as in Fig. 17
Finally in Fig. 19 we show the \({\tilde{l}}^{\pm }\)-coannihilation Case-R. As argued in the previous subsection, in this case some EW SUSY particles are driven to relatively low mass values. This is visible in Fig. 19, where the left (right) plot shows the cross-section predictions for \(e^+e^- \rightarrow {\tilde{\chi }}_{1}^0{\tilde{\chi }}_{2}^0\) and \(e^+e^- \rightarrow {\tilde{\mu }}_{2}{\tilde{\mu }}_{2}\) with the same symbol/color coding as in Fig. 17. In the case of \({\tilde{\chi }}_{1}^0{\tilde{\chi }}_{2}^0\) production even with the current \((g-2)_\mu \) constraint a collider with \(\sqrt{s} = 1500 \,\, \mathrm {GeV}\) is sufficient to cover the full spectrum. With the anticipated future \((g-2)_\mu \) accuracy only mass sum values \(\lesssim 800 \,\, \mathrm {GeV}\) are reached, and even the ILC500 can cover a relevant part of the spectrum. Most cross-sections are at or above \(10^{-3}\) pb, i.e. at least 1000 events per \(\text {ab}^{-1}\) would be produced. The situation is similar for \({\tilde{\mu }}_{2}{\tilde{\mu }}_{2}\) production, although with even higher production cross-sections. The ILC1000 could cover the full spectrum corresponding to the anticipated future \((g-2)_\mu \) accuracy, and some part of the spectrum would be accessible even at the ILC350 (or circular \(e^+e^-\) colliders reaching this energy).
The above shown example cross-sections clearly show the anticipated future accuracy on \((g-2)_\mu \) has the power to sharpen the upper limits on EW SUSY particles sufficiently, such that at least some particles are guaranteed to be discovered at the higher-energy stages of the ILC and/or CLIC. (The LSP should be accessible in almost any case even with the current \((g-2)_\mu \) accuracy.) If the future \((g-2)_\mu \) constraint confirms the deviation of \(a_\mu ^{\mathrm{exp}}\) from the SM prediction, the case for future \(e^+e^-\) colliders is clearly strengthened.
As discussed in Sect. 4.1 we have not considered the possibility of Z or h pole annihilation to find agreement of the relic DM density with the other experimental measurements. However, it should be noted that in this context an LSP with \(M_1 \sim m_{{\tilde{\chi }}_{1}^0} \sim M_Z/2\) or \(\sim M_h/2\) would yield a detectable cross-section \(e^+e^- \rightarrow {\tilde{\chi }}_{1}^0{\tilde{\chi }}_{1}^0\gamma \) in any future high-energy \(e^+e^-\) collider. Furthermore, depending on the values of \(M_2\) and \(\mu \), this scenario likely yields other clearly detectable EW-SUSY production cross-sections at future \(e^+e^-\) colliders. We leave this possibility for future studies.
On the other hand, the possibility of A-pole annihilation was discussed for all three scenarios. While it appears a rather remote possibility, it cannot be fully excluded by our analysis. However, even in the “worst” case of \({\tilde{l}}^{\pm }\)-coannihilation Case-L an upper limit on \(m_{{\tilde{\chi }}_{1}^0}\) of \(\sim 260 \,\, \mathrm {GeV}\) can be set. While not as low as in the case of Z or h-pole annihilation, this would still offer good prospects for future \(e^+e^-\) colliders. We leave also this possibility for future studies.
7 Conclusions
The electroweak (EW) sector of the MSSM, consisting of charginos, neutralinos and scalar leptons can account for a variety of experimental data. Concerning the CDM relic abundance, the MSSM offers a natural candidate, the lightest neutralino, \({\tilde{\chi }}_{1}^0\), while satisfying the bounds from DD experiments which have yielded negative results so far. As a result of comparatively small production cross-sections, a relatively light EW sector of the MSSM is also in agreement with the latest experimental exclusion limits from the LHC. Most importantly, the EW sector of the MSSM can account for the long-standing \(3-4\,\sigma \) discrepancy of \((g-2)_\mu \). Improved experimental results are expected in the course of 2020 by the publication of the Run 1 data of the “MUON G-2” experiment.
In this paper, under the assumption that the \({\tilde{\chi }}_{1}^0\) provides the full DM relic abundance we first analyzed which mass ranges of neutralinos, charginos and sleptons are in agreement with all relevant experimental data: the current limit for \((g-2)_\mu \) , the relic density bounds, the DD experimental bounds, as well as the LHC searches for EW SUSY particles. Concerning the latter we included all relevant existing data, mostly relying on re-casting via CheckMATE, where several channels had to be newly implemented. We analyzed three scenarios, depending on the mechanism that brings the relic density in agreement with the experimental data: \({\tilde{\chi }}_{1}^\pm \)-coannihilation, \({\tilde{l}}^{\pm }\)-coannihilation with the mass of the “left-handed” (“right-handed”) slepton close to \(m_{{\tilde{\chi }}_{1}^0}\), Case-L (Case-R). We find in all three cases a clear upper limit on \(m_{{\tilde{\chi }}_{1}^0}\). While for \({\tilde{\chi }}_{1}^\pm \)-coannihilation this is \(\sim 570 \,\, \mathrm {GeV}\), for \({\tilde{l}}^{\pm }\)-coannihilation Case-L \(\sim 540 \,\, \mathrm {GeV}\) and for Case-R values up to \(\sim 520 \,\, \mathrm {GeV}\) are allowed. Similarly, upper limits to masses of the coannihilating SUSY particles are found as, \(m_{{\tilde{\chi }}_{1}^\pm } \lesssim 610 \,\, \mathrm {GeV}\), \(m_{{\tilde{l}}_{L}} \lesssim 550 \,\, \mathrm {GeV}\), \(m_{{\tilde{l}}_{R}} \lesssim 590 \,\, \mathrm {GeV}\). For the latter, in the \({\tilde{l}}^{\pm }\)-coannihilation case-R, the upper limit on the lighter \({\tilde{\tau }}\) is even lower, \(m_{\tilde{\tau }_{2}} \lesssim 530 \,\, \mathrm {GeV}\). The current \((g-2)_\mu \) constraint also yields limits on the rest of the EW spectrum, although much loser bounds are found. As an example, for \({\tilde{\chi }}_{1}^\pm \)-coannihilation we find \(m_{{\tilde{l}}_{L}} \lesssim 900 \,\, \mathrm {GeV}\), for \({\tilde{l}}^{\pm }\)-coannihilation Case-L \(m_{{\tilde{\chi }}_{1}^\pm } \lesssim 3 \,\, \mathrm {TeV}\) and \(m_{{\tilde{\chi }}_{1}^\pm } \lesssim 1 \,\, \mathrm {TeV}\) for Case-R. These upper bounds set clear collider targets for the HL-LHC and future \(e^+e^-\) colliders.
In a second step we assumed that the new result of the Run 1 of the “MUON G-2” collaboration at Fermilab yields a precision comparable to the existing experimental result with the same central value. We analyzed the potential impact of the combination of the Run 1 data with the existing result on the allowed MSSM parameter space. We find that the upper limits on the LSP mass are decreased to about \(425 \,\, \mathrm {GeV}\) for \({\tilde{\chi }}_{1}^\pm \)-coannihilation, \(500 \,\, \mathrm {GeV}\) for \({\tilde{l}}^{\pm }\)-coannihilation Case-L and \(400 \,\, \mathrm {GeV}\) in Case-R, sharpening the collider targets substantially. Similarly, the upper limits on the NLSP masses go down to about \(470 \,\, \mathrm {GeV}\), \(510 \,\, \mathrm {GeV}\) and \(410 \,\, \mathrm {GeV}\) in the three cases that we have explored.
For the HL-LHC we have briefly reviewed the anticipated future upper limits and \(5\,\sigma \) discovery regions. We find that the chargino/neutralino production at the HL-LHC via on-shell W and Higgs decays have a substantial impact on the allowed parameter space of \({\tilde{l}}^{\pm }\)-coannihilation scenarios. In particular, the fate of Case-R can be conclusively determined with only this search channel. On the other hand, the compressed spectrum searches for chargino-neutralino production may become important to probe the parameter space of \({\tilde{\chi }}_{1}^\pm \)-coannihilation region.
Concerning future high(er) energy \(e^+e^-\) colliders, we have evaluated the production cross-sections for the anticipated center-of-mass energies of ILC and CLIC. The LSP should be accessible in almost any case at \(\sqrt{s} = 1000 \,\, \mathrm {GeV}\) even with the current \((g-2)_\mu \) accuracy and can effectively be fully covered with the anticipated future accuracy. Moreover, since the anticipated future accuracy on \((g-2)_\mu \) has the potential to narrow down the upper limits on EW SUSY particles sufficiently, the analyzed example cross-sections show that at least some particles are guaranteed to be discovered at the higher-energy stages of the ILC and/or CLIC. Therefore, if the future \((g-2)_\mu \) constraints confirms the deviation of \(a_\mu ^{\mathrm{exp}}\) from the SM prediction, our findings strongly motivate the need of future \(e^+e^-\) colliders.
While we have attempted to cover nearly the full set of possibilities that the EW spectrum of the MSSM can fulfill all the various experimental constraints, our studies can be extended/completed in the following ways. One can analyze the cases of: (i) complex parameters in the chargino/neutralino sector (then also taking EDM constraints into account); (ii) different soft SUSY-breaking parameters in the three generations of sleptons, and/or between the left- and right-handed entries in the case of \({\tilde{\chi }}_{1}^\pm \)-coannihilation; (iii) A-pole annihilation, in particular in the case of \({\tilde{l}}^{\pm }\)-coannihilation for very low \(m_{{\tilde{\chi }}_{1}^0}\) and \(\tan \beta \) values; (iv) h- and Z-pole annihilation, which could be realized for sufficiently heavy sleptons; (v) requiring the CDM constraint only as upper limit. We leave these analyses for future work.
In this paper we have analyzed in particular the impact of \((g-2)_\mu \) measurements on the EW SUSY spectrum. While the current experimental and theoretical situation is clear, the upcoming measurements of the “MUON G-2” collaboration were shown to have the strong potential of sharpening the future collider experiment prospects. All this hinges, of course, on the central value the collaboration will observe (where we used the simplest assumption of the same central value as in the current experimental data). We are eagerly awaiting the new “MUON G-2” result to illuminate further the possibility of relatively light EW BSM particles.
Data Availability Statement
This manuscript has no associated data or the data will not be deposited. [Authors’ comment: There is no additional data or the data is already included in the manuscript].
Notes
In the context of LHC searches, we use leptons to imply only the first two generations unless otherwise mentioned.
The \(\text {BR}({\tilde{\chi }}_{2}^0 \rightarrow h {\tilde{\chi }}_{1}^0)\) increases from \(\sim \) 55% at the kinematic threshold \((m_{{\tilde{\chi }}_{2}^0}-m_{{\tilde{\chi }}_{1}^0}) \sim 125 \,\, \mathrm {GeV}\) to \(\sim 80\%\) for slightly larger mass splittings for a predominantly wino-like \({\tilde{\chi }}_{2}^0\).
We have also checked our points surviving all other constraints against vacuum stability, in particular taking into account the scalar tau sector [103], which can become relevant for large \(\mu \tan \beta \). We found that all our surviving points pass this constraint.
Stronger limits using \(139\, \text {fb}^{-1}\) have recently become available [108]. However, no evaluation in the \(M_h^{125}({\tilde{\chi }})\) is available yet.
References
A. Keshavarzi, D. Nomura, T. Teubner, Phys. Rev. D 101(1), 014029 (2020). arXiv:1911.00367 [hep-ph]
M. Davier, A. Hoecker, B. Malaescu, Z. Zhang, arXiv:1908.00921 [hep-ph]
J. Grange et al. [Muon g-2 Collaboration], arXiv:1501.06858 [physics.ins-det]
N. Aghanim et al. [Planck Collaboration], arXiv:1807.06209 [astro-ph.CO]
D.S. Akerib et al. [LUX Collaboration], Phys. Rev. Lett. 118(2), 021303 (2017). arXiv:1608.07648 [astro-ph.CO]
X. Cui et al. [PandaX-II Collaboration], Phys. Rev. Lett. 119(18), 181302 (2017). arXiv:1708.06917 [astro-ph.CO]
E. Aprile et al. [XENON Collaboration], Phys. Rev. Lett. 121(11), 111302 (2018).arXiv:1805.12562 [astro-ph.CO]
H. Nilles, Phys. Rep. 110, 1 (1984)
R. Barbieri, Riv. Nuovo Cim. 11, 1 (1988)
H. Haber, G. Kane, Phys. Rep. 117, 75 (1985)
J. Gunion, H. Haber, Nucl. Phys. B 272, 1 (1986)
H. Goldberg, Phys. Rev. Lett. 50, 1419 (1983)
J. Ellis, J. Hagelin, D. Nanopoulos, K. Olive, M. Srednicki, Nucl. Phys. B 238, 453 (1984)
A. Bharucha, S. Heinemeyer, F. von der Pahlen, Eur. Phys. J. C 73(11), 2629 (2013). arXiv:1307.4237 [hep-ph]
T. Han, S. Padhi, S. Su, Phys. Rev. D 88(11), 115010 (2013). arXiv:1309.5966 [hep-ph]
A. Choudhury, S. Mondal, Phys. Rev. D 94(5), 055024 (2016). arXiv:1603.05502 [hep-ph]
A. Datta, N. Ganguly, S. Poddar, Phys. Lett. B 763, 213–217 (2016). arXiv:1606.04391 [hep-ph]
M. Chakraborti, A. Datta, N. Ganguly, S. Poddar, JHEP 1711, 117 (2017). arXiv:1707.04410 [hep-ph]
K. Hagiwara, K. Ma, S. Mukhopadhyay, Phys. Rev. D 97(5), 055035 (2018). arXiv:1706.09313 [hep-ph]
T.T. Yanagida, W. Yin, N. Yokozaki, JHEP 06, 154 (2020). https://doi.org/10.1007/JHEP06(2020)154. arXiv:2001.02672 [hep-ph]
W. Yin, N. Yokozaki, Phys. Lett. B 762, 72–79 (2016). https://doi.org/10.1016/j.physletb.2016.09.024. arXiv:1607.05705 [hep-ph]
T.T. Yanagida, W. Yin, N. Yokozaki, JHEP 09, 086 (2016). https://doi.org/10.1007/JHEP09(2016)086. arXiv:1608.06618 [hep-ph]
M. Chakraborti, U. Chattopadhyay, S. Poddar, JHEP 1709, 064 (2017). arXiv:1702.03954 [hep-ph]
S. Abdus Salam et al., Eur. Phys. J. C 71, 1835 (2011). arXiv:1109.3859 [hep-ph]
E.A. Bagnaschi et al., Eur. Phys. J. C 75, 500 (2015). arXiv:1508.01173 [hep-ph]
A. Datta, N. Ganguly, JHEP 1801, 103 (2019). arXiv:1809.05129 [hep-ph]
P. Cox, C. Han, T.T. Yanagida, Phys. Rev. D 98(5), 055015 (2018). arXiv:1805.02802 [hep-ph]
P. Cox, C. Han, T.T. Yanagida, N. Yokozaki, JHEP 08, 097 (2019). arXiv:1811.12699 [hep-ph]
M. Abdughani, K. Hikasa, L. Wu, J.M. Yang, J. Zhao, JHEP 1911, 095 (2019). arXiv:1909.07792 [hep-ph]
M. Endo, K. Hamaguchi, S. Iwamoto, T. Kitahara, JHEP 2004, 165 (2020). arXiv:2001.11025 [hep-ph]
G. Pozzo, Y. Zhang, Phys. Lett. B 789, 582–591 (2019). arXiv:1807.01476 [hep-ph]
P. Athron et al. [GAMBIT], Eur. Phys. J. C 79(5), 395 (2019). arXiv:1809.02097 [hep-ph]
M. Drees, H. Dreiner, D. Schmeier, J. Tattersall, J.S. Kim, Comput. Phys. Commun. 187, 227–265 (2015). arXiv:1312.2591 [hep-ph]
J.S. Kim, D. Schmeier, J. Tattersall, K. Rolbiecki, Comput. Phys. Commun. 196, 535–562 (2015). arXiv:1503.01123 [hep-ph]
D. Dercks, N. Desai, J.S. Kim, K. Rolbiecki, J. Tattersall, T. Weber, Comput. Phys. Commun. 221, 383–418 (2017). arXiv:1611.09856 [hep-ph]
H. Baer et al., The International Linear Collider Technical Design Report, Vol. 2: Physics. arXiv:1306.6352 [hep-ph]
G. Moortgat-Pick et al., Eur. Phys. J. C 75, 8, 371 (2015). arXiv:1504.01726 [hep-ph]
L. Linssen, A. Miyamoto, M. Stanitzki, H. Weerts, arXiv:1202.5940 [physics.ins-det]
H. Abramowicz et al. [CLIC Detector and Physics Study Collaboration], arXiv:1307.5288 [hep-ex]
P. Burrows et al. [CLICdp and CLIC Collaborations], CERN Yellow Rep. Monogr. 1802, 1 (2018). arXiv:1812.06018 [physics.acc-ph]
See: https://twiki.cern.ch/twiki/bin/view/AtlasPublic/SupersymmetryPublicResults
See: https://twiki.cern.ch/twiki/bin/view/CMSPublic/PhysicsResultsSUS
E. Bagnaschi et al., Eur. Phys. J. C 78(3), 256 (2018). arXiv:1710.11091 [hep-ph]
M. Aaboud et al. [ATLAS], Eur. Phys. J. C 78(12), 995 (2018). arXiv:1803.02762 [hep-ex]
G. Aad et al. [ATLAS Collaboration], Eur. Phys. J. C 80(2), 123 (2020). arXiv:1908.08215 [hep-ex]
A. Sirunyan et al. [CMS], JHEP 2018, 166 (1803). arXiv:1709.05406 [hep-ex]
A. Sirunyan et al. [CMS], JHEP 2018, 160 (1803). arXiv:1801.03957 [hep-ex]
G. Aad et al. [ATLAS Collaboration], arXiv:1909.09226 [hep-ex]
A.M. Sirunyan et al. [CMS], JHEP 11, 029 (2017). arXiv:1706.09933 [hep-ex]
A.M. Sirunyan et al. [CMS], Phys. Lett. B 790, 140–166 (2019).arXiv:1806.05264 [hep-ex]
G. Aad et al. [ATLAS Collaboration], arXiv:1911.12606 [hep-ex]
A.M. Sirunyan et al. [CMS], Phys. Lett. B 782, 440–467 (2018). arXiv:1801.01846 [hep-ex]
G. Aad et al. [ATLAS], Phys. Rev. D 101(3), 032009 (2020). arXiv:1911.06660 [hep-ex]
J. Alwall, R. Frederix, S. Frixione, V. Hirschi, F. Maltoni, O. Mattelaer, H. Shao, T. Stelzer, P. Torrielli, M. Zaro, JHEP 1407, 079 (2014). arXiv:1405.0301 [hep-ph]
T. Sjöstrand, S. Ask, J.R. Christiansen, R. Corke, N. Desai, P. Ilten, S. Mrenna, S. Prestel, C.O. Rasmussen, P.Z. Skands, Comput. Phys. Commun. 191, 159–177 (2015). arXiv:1410.3012 [hep-ph]
R.D. Ball, V. Bertone, S. Carrazza, C.S. Deans, L. Del Debbio, S. Forte, A. Guffanti, N.P. Hartland, J.I. Latorre, J. Rojo, M. Ubiali, Nucl. Phys. B 867, 244–289 (2013). arXiv:1207.1303 [hep-ph]
L. Lönnblad, S. Prestel, JHEP 03, 166 (2013). arXiv:1211.7278 [hep-ph]
M. Cacciari, G.P. Salam, Phys. Lett. B 641, 57–61 (2006). arXiv:hep-ph/0512210 [hep-ph]
M. Cacciari, G.P. Salam, G. Soyez, Eur. Phys. J. C 72, 1896 (2012). arXiv:1111.6097 [hep-ph]
J. de Favereau et al. [DELPHES 3], JHEP 1402, 057 (2014). arXiv:1307.6346 [hep-ex]
G.W. Bennett et al. [Muon g-2 Collaboration], Phys. Rev. D 73, 072003 (2006). arXiv:hep-ex/0602035
M. Tanabashi et al. [Particle Data Group], Phys. Rev. D 98(3), 030001 (2018)
T. Aoyama et al., arXiv:2006.04822 [hep-ph]
T. Mibe [J-PARC g-2 Collaboration], Chin. Phys. C 34, 745 (2010)
S. Borsanyi et al., arXiv:2002.12347 [hep-lat]
F. Jegerlehner, EPJ Web Conf. 166, 00022 (2018). arXiv:1705.00263 [hep-ph]
C. Lehner, A.S. Meyer, arXiv:2003.04177 [hep-lat]
A. Crivellin, M. Hoferichter, C.A. Manzari, M. Montull, arXiv:2003.04886 [hep-ph]
A. Keshavarzi, W.J. Marciano, M. Passera, A. Sirlin, arXiv:2006.12666 [hep-ph]
E. de Rafael, arXiv:2006.13880 [hep-ph]
T. Moroi, Phys. Rev. D 53, 6565 (1996) [Erratum: Phys. Rev. D 56, 4424 (1997)]. arXiv:hep-ph/9512396
S.P. Martin, J.D. Wells, Phys. Rev. D 64, 035003 (2001). arXiv:hep-ph/0103067
M. Badziak, K. Sakurai, JHEP 1910, 024 (2019). arXiv:1908.03607 [hep-ph]
P. Athron et al., Eur. Phys. J. C 76(2), 62 (2016). arXiv:1510.08071 [hep-ph]
P. von Weitershausen, M. Schafer, H. Stockinger-Kim, D. Stockinger, Phys. Rev. D 81, 093004 (2010). arXiv:1003.5820 [hep-ph]
H. Fargnoli, C. Gnendiger, S. Paßehr, D. Stöckinger, H. Stöckinger-Kim, JHEP 1402, 070 (2014). arXiv:1311.1775 [hep-ph]
M. Bach, Jh Park, D. Stöckinger, H. Stöckinger-Kim, JHEP 1510, 026 (2015). arXiv:1504.05500 [hep-ph]
S. Heinemeyer, D. Stockinger, G. Weiglein, Nucl. Phys. B 690, 62–80 (2004). arXiv:hep-ph/0312264 [hep-ph]
S. Heinemeyer, D. Stockinger, G. Weiglein, Nucl. Phys. B 699, 103–123 (2004). arXiv:hep-ph/0405255 [hep-ph]
J. Hisano, S. Matsumoto, M. Nagai, O. Saito, M. Senami, Phys. Lett. B 646, 34 (2007). arXiv:hep-ph/0610249
M. Cirelli, A. Strumia, M. Tamburini, Nucl. Phys. B 787, 152 (2007). arXiv:0706.4071 [hep-ph]
A. Hryczuk, R. Iengo, P. Ullio, JHEP 1103, 069 (2011). arXiv:1010.2172 [hep-ph]
M. Beneke, A. Bharucha, F. Dighera, C. Hellmann, A. Hryczuk, S. Recksiegel, P. Ruiz-Femenia, JHEP 1603, 119 (2016). arXiv:1601.04718 [hep-ph]
E. Bagnaschi et al., Eur. Phys. J. C 77(4), 268 (2017). arXiv:1612.05210 [hep-ph]
N. Arkani-Hamed, A. Delgado, G.F. Giudice, Nucl. Phys. B 741, 108 (2006). arXiv:hep-ph/0601041
G. Belanger, F. Boudjema, A. Pukhov, A. Semenov, Comput. Phys. Commun. 149, 103–120 (2002). arXiv:hep-ph/0112278 [hep-ph]
G. Belanger, F. Boudjema, A. Pukhov, A. Semenov, Comput. Phys. Commun. 176, 367–382 (2007). arXiv:hep-ph/0607059 [hep-ph]
G. Belanger, F. Boudjema, A. Pukhov, A. Semenov, Comput. Phys. Commun. 177, 894–895 (2007). [87]
G. Belanger, F. Boudjema, A. Pukhov, A. Semenov, arXiv:1305.0237 [hep-ph]
J. Hisano, K. Nakayama, M. Yamanaka, Phys. Lett. B 684, 246 (2010). arXiv:0912.4701 [hep-ph]
J. Billard, L. Strigari, E. Figueroa-Feliciano, Phys. Rev. D 89(2), 023524 (2014). arXiv:1307.5458 [hep-ph]
P. Cushman et al., arXiv:1310.8327 [hep-ex]
N.W. Evans, C.A.J. O’Hare, C. McCabe, arXiv:1810.11468 [astro-ph.GA]
G.H. Duan, K.I. Hikasa, J. Ren, L. Wu, J.M. Yang, Phys. Rev. D 98(1), 015010 (2018). arXiv:1804.05238 [hep-ph]
C. Cheung, L.J. Hall, D. Pinner, J.T. Ruderman, JHEP 1305, 100 (2013). arXiv:1211.4873 [hep-ph]
T. Han, F. Kling, S. Su, Y. Wu, JHEP 1702, 057 (2017). arXiv:1612.02387 [hep-ph]
A. Crivellin, M. Hoferichter, M. Procura, L.C. Tunstall, JHEP 07, 129 (2015). arXiv:1503.03478 [hep-ph]
E. Aprile et al. [XENON], Phys. Rev. Lett. 122(14), 141301 (2019). arXiv:1902.03234 [astro-ph.CO]
C. Amole et al. [PICO], Phys. Rev. D 100(2), 022001 (2019). arXiv:1902.04031 [astro-ph.CO]
K.J. de Vries et al., Eur. Phys. J. C 75(9), 422 (2015). arXiv:1504.03260 [hep-ph]
A. Djouadi, J.L. Kneur, G. Moultaka, Comput. Phys. Commun. 176, 426 (2007). arXiv:hep-ph/0211331
Joint LEP2 SUSY Working Group, the ALEPH, DELPHI, L3 and OPAL Collaborations. http://lepsusy.web.cern.ch/lepsusy/
M. Endo, K. Hamaguchi, T. Kitahara, T. Yoshinaga, JHEP 11, 013 (2013). arXiv:1309.3065 [hep-ph]
M. Muhlleitner, A. Djouadi, Y. Mambrini, Comput. Phys. Commun. 168, 46 (2005). arXiv:hep-ph/0311167
E. Bagnaschi et al., Eur. Phys. J. C 79(7), 617 (2019). arXiv:1808.07542 [hep-ph]
M. Aaboud et al. [ATLAS], JHEP 1801, 055 (2018). arXiv:1709.07242 [hep-ex]
A.M. Sirunyan et al. [CMS], JHEP 1809, 007 (2018). arXiv:1803.06553 [hep-ex]
G. Aad et al. [ATLAS], arXiv:2002.12223 [hep-ex]
X Cid Vidal et al., CERN Yellow Rep. Monogr. 7, 585–865 (2019). arXiv:1812.07831 [hep-ph]
S. Heinemeyer, C. Schappacher, Eur. Phys. J. C 77(9), 649 (2017). arXiv:1704.07627 [hep-ph]
S. Heinemeyer, C. Schappacher, Eur. Phys. J. C 78(7), 536 (2018). arXiv:1803.10645 [hep-ph]
T. Fritzsche, T. Hahn, S. Heinemeyer, F. von der Pahlen, H. Rzehak, C. Schappacher, Comput. Phys. Commun. 185, 1529–1545 (2014). arXiv:1309.1692 [hep-ph]
M. Berggren, arXiv:1308.1461 [hep-ph]
M.T.N. Pardo de Vera, M. Berggren, J. List, arXiv:2002.01239 [hep-ph]
M. Berggren, arXiv:2003.12391 [hep-ph]
H. Baer, M. Berggren, K. Fujii, J. List, S.L. Lehtinen, T. Tanabe, J. Yan, Phys. Rev. D 101(9), 095026 (2020). arXiv:1912.06643 [hep-ex]
T. Barklow, J. Brau, K. Fujii, J. Gao, J. List, N. Walker, K. Yokoya, arXiv:1506.07830 [hep-ex]
K. Fujii et al., arXiv:1710.07621 [hep-ex]
A. Robson, P. Roloff, arXiv:1812.01644 [hep-ex]
J. de Blas et al., JHEP 01, 139 (2020). arXiv:1905.03764 [hep-ph]
Acknowledgements
We thank M. D’Onofrio, J. List and D. Stöckinger for helpful discussions. We thank J. S. Kim for help with the implementation of new LHC search channels to CheckMATE. We thank C. Schappacher for the calculation of the \(e^+e^-\) EW-SUSY production cross-sections. I.S. gratefully thanks S. Matsumoto for the cluster facility. I.S. acknowledges the warm hospitality of the IFT, Madrid and thanks the organizers of the workshop “Opportunities at Future High Energy Colliders” for the invitation where this work was initiated. The work of I.S. is supported by World Premier International Research Center Initiative (WPI), MEXT, Japan. The work of S.H. is supported in part by the Spanish Agencia Estatal de Investigación (AEI) and the EU Fondo Europeo de Desarrollo Regional (FEDER) through the project FPA2016-78645-P and in part by the “Spanish Red Consolider MultiDark” FPA2017-90566-REDC. The work of M.C. and S.H. is supported in part by the MEINCOP Spain under contract FPA2016-78022-P and in part by the AEI through the grant IFT Centro de Excelencia Severo Ochoa SEV-2016-0597.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3
About this article
Cite this article
Chakraborti, M., Heinemeyer, S. & Saha, I. Improved \((g-2)_\mu \) measurements and supersymmetry. Eur. Phys. J. C 80, 984 (2020). https://doi.org/10.1140/epjc/s10052-020-08504-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-020-08504-8


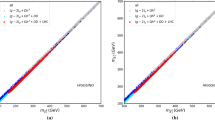






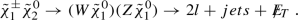



 (i.e. requiring a leptonic
(i.e. requiring a leptonic