NANOGrav and other PTA signals and PBH from the modified Higgs inflation

Abstract

This study investigates the classical Higgs inflation model with a modified Higgs potential featuring a dip. We examine the implications of this modification on the generation of curvature perturbations, stochastic gravitational wave production, and the potential formation of primordial black holes (PBHs). Unlike the classical model, the modified potential allows for enhanced power spectra and the existence of PBHs within a wide mass range $1.5\times 10^{20}$ g–$9.7\times 10^{32}$ g. We identify parameter space regions that align with inflationary constraints and have the potential to contribute significantly to the observed dark matter content. Additionally, the study explores the consistency of the obtained parameter space with cosmological constraints and discusses the implications for explaining the observed excess in gravitational wave PTA signals, particularly in the NANOGrav experiment. Overall, this investigation highlights the relevance of the modified Higgs potential in the classical Higgs inflation model, shedding light on the formation of PBHs, the nature of dark matter, and the connection to gravitational wave observations.

1 Introduction

Cosmological inflation is the most favorable theory of the early universe [1]. It not only explains the absence of a number of relics that should have existed from the Big Bang, but also provides the seeds for the growth of structures in the Universe. In the last two decades, people have been attempting to figure out the most promising candidate for cosmological inflation.

Primordial black holes (PBHs) can also be created as a result of cosmological inflation, potentially generating PBHs from the seeds formed during the radiation- or matter-dominated epochs. Consequently, studying the formation and evolution of PBHs offers an effective means to investigate the early period of cosmology. The existence of primordial black holes was initially postulated by Zel’dovich and Novikov [2], and later supported by Hawking and Carr [3,4,5], suggesting that these hypothetical entities emerged in the early universe. According to the theory, PBHs may form in the regions with significant density perturbations. The primary motivation for studying PBHs lies in their potential as a natural candidate for dark matter. Despite recent observations imposing strict limitations on the abundance of PBHs, there exists a mass range, specifically from $10^{16}$ g to $10^{20}$ g, where PBHs could play a significant role in contributing to the overall dark matter content.

Production of gravitational waves through the second-order effect is closely intertwined with the formation of PBHs, occurring simultaneously as certain modes re-enter the Hubble radius. These gravitational waves, once generated, propagate freely throughout subsequent epochs of the Universe due to their low interaction rate.

Millisecond pulsars (MPs) are featured by their stable rotating periods which are comparable to the timing precision of atomic clocks. They are ideal astrophysical objects being utilized in the pulsar-timing arrays (PTAs) to probe the low-frequency gravitation waves (GWs) from nanohertz to microhertz. Currently, a number of PTA’s are taking data: NANOGrav [6, 7], PPTA [8], EPTA and InPTA [9], CPTA [10], and International PTA [11]. All these PTA collaborations have reported strong evidence for a nanohertz gravitational-wave background. In this work, we focus on the data given by the NANOGrav collaboration. The NANOGrav collaboration has been observing 67 pulsars over 15 years and recently reported evidence for the correlations following Hellings–Downs pattern [6], pointing to the stochastic GW as the origin. Furthermore, they confirmed the excess of the red common-spectrum signal with a strain amplitude of $\mathcal {O}(10^{-14})$ at the frequency $\simeq 3\times 10^{-8}$ Hz. To explain the GW signal, there are many plausible mechanisms and hypothetical candidates being proposed; in particular, the population of supermassive black-hole binarys [6, 7, 12, 13], inflation scenarios [14,15,16,17,18,19,20,21,22], cosmological first-order phase transition [23,24,25,26,27,28,29,30], and alternative interpretations [31,32,33,34,35,36].

There have been numerous attempts to incorporate inflation into the standard model (SM) and theories beyond. The SM Higgs field has always been an intriguing candidate as the inflaton due to its lack of requirement for additional scalar degrees of freedom. However, the minimal Higgs inflation model is not favored, and possibly even ruled out, due to the fine-tuned value of the Higgs self-coupling constant, $\lambda$. To address this issue, a non-minimal coupling between the SM Higgs field and the Ricci scalar, $\mathcal {R}$, was introduced in an attempt to reduce the value of $\lambda$ [37]. However, such attempts may potentially lead to violations of unitarity [38,39,40], although our current study does not focus on these infractions.

The fundamental Higgs inflation model [37] fails to account for both the inflationary phase and the formation of PBHs simultaneously. Numerous studies have explored both inflation and PBH formation within the framework of Higgs inflation by introducing new interactions to the Higgs field. By incorporating these additional interactions, it is possible to achieve a successful inflationary epoch while creating the conditions necessary for the generation of PHBs. In this investigation, we examine a modified form of the Higgs potential that aims to address both the phenomenon of inflation and the formation of PBHs, and at the same time address the excess in GW signal reported by NANOGrav.

The paper is organized as follows. In Sect. 2, we revisit the classical Higgs inflation model and demonstrate that it is incapable of generating the correct power spectrum required for PBH formation. In Sect. 3, we delve into possible modifications to the Higgs potential. Specifically, we explore the introduction of a dip in the potential, which can accommodate PBH formation during the inflationary scenario. We also discuss the viable parameter space by considering the characteristics of the dip for PBH formation. With the presence of the dip in the scalar potential, the slow-roll conditions may not be valid. Thus, we use the exact formulas for calculating the scalar power spectrum. We show the comparison between the slow-roll approximation and the exact calculation in Appendix D. Sections 4 and 5 are dedicated to presenting the PBH abundance and gravitational wave (GW) spectrum resulting from the modified Higgs potential. In Sect. 5, we discuss the gravitational wave signals within this model and demonstrate that the obtained results can potentially explain the NANOGrav 15-year signal in a straightforward manner. We conclude with the implications of these findings. We show more details of our calculation in Appendix A, the corresponding results of a bump in Appendix B, the PBH abundance versus the width of the dip in Appendix C, and the comparison between the slow-roll approximation and the exact calculation in Appendix D.

2 Revisiting Higgs inflation model

In this section, we revisit the classical Higgs Inflation model, which considers the SM Higgs Boson as a promising candidate for inflation. The Higgs inflation model [37] was proposed a long time ago to bridge the gap between the two most successful models of physics: the standard model of particle physics and the standard model of cosmology. Numerous studies [41,42,43,44,45,46,47] discussed the possibility of the SM Higgs as the inflaton in different contexts.

In our discussion, we focus on the simplest model of Higgs Inflation [37]. This model addresses inflation by introducing a non-minimal coupling, where the SM Higgs is coupled to the Ricci scalar $\mathcal {R}$ with a non-minimal coupling strength $\xi$. The effective action for this theory is given as

$$\begin{aligned} \mathcal {S_J}=\int ~d^4x~\sqrt{-g}\left[ -\frac{M_\textrm{PL}^2+\xi h^2}{2}\mathcal {R} +\frac{\partial _{\mu }h\partial ^{\mu }h}{2}-\frac{\lambda }{4}(h^2-v^2)^2 \right] .\nonumber \\ \end{aligned}$$

(1)

This Lagrangian has been studied in details in many works on inflation [48,49,50]. The scalar sector of the SM coupled to the gravity in a non-minimal way. Here the authors considered the unitary gauge $H=\frac{h}{\sqrt{2}}$ and neglected the interactions for the time being. An action in the Einstein frame was obtained by the conformal transformation [51, 52] $\hat{g} _{\mu \nu }=\Omega g_{\mu \nu }$, where $\Omega =1+\frac{\xi h^2}{M^2_\textrm{PL}}$. The conformal transformation can eliminate the non-minimal coupling to gravity. This transformation leads to a non-minimal kinetic term for the Higgs field. So, it is convenient to make the change to the new scalar field $\phi$ with

$$\begin{aligned} \frac{d\phi }{dh}=\sqrt{\frac{\Omega }{\Omega ^2}+\frac{3M^2_\textrm{PL}}{2}\frac{(\frac{d\Omega }{dh})^2}{\Omega ^2}} \end{aligned}$$

(2)

The action in the Einstein frame is

$$\begin{aligned} \mathcal {S_E}=\int d^4x \sqrt{-\hat{g}}\big [-\frac{M^2_\textrm{PL}}{2}\mathcal {\hat{R}}+\frac{\partial _{\mu }\phi \partial ^{\mu }\phi }{2}-U(\phi )\big ]. \end{aligned}$$

(3)

The exponentially flat effective potential for the Higgs field is given by

$$\begin{aligned} U(\phi )=\frac{\lambda M^2_{PL}}{4\xi ^2}\Bigg (1+\text {exp}\Big (- \frac{2\phi }{\sqrt{6}M_{PL}} \Big ) \Bigg )^{-2} \end{aligned}$$

(4)

The slow-roll parameters of this model of inflation can be expressed as the function of $h(\phi )$ as follows

$$\begin{aligned} \epsilon =\frac{M^2_\textrm{PL}}{2}\Bigg (\frac{\frac{\partial U}{\partial \phi }}{U} \Bigg )^2=\frac{4 M^4_\textrm{PL}}{3\xi ^2 h^4} \end{aligned}$$

(5)

$$\begin{aligned} \eta =M^2_\textrm{PL}\Bigg (\frac{\frac{\partial ^2U}{\partial \phi ^2}}{U}\Bigg )=-\frac{4M^2_\textrm{Pl}}{3\xi h^2}. \end{aligned}$$

(6)

The slow roll ends when $\epsilon =1$, the field value at the end of inflation is given by,

$$\begin{aligned} h_{end}=\Big (\frac{4}{3}\Big )^{\frac{1}{4}} \Big (\frac{M_\textrm{PL}}{\sqrt{\xi }}\Big ). \end{aligned}$$

(7)

The number of e-folds that are required to change the field h from $h_{int}$ to $h_{end}$ is given by

$$\begin{aligned} N_{e}=\int _{h_{end}}^{h_{int}}\frac{1}{M_\textrm{PL}^2} \Bigg (\frac{U}{\frac{\partial U}{\partial h}} \left( \frac{\partial \phi }{\partial h}\right) ^2\Bigg ) dh . \end{aligned}$$

(8)

The field value $h_{int}$ at the beginning of inflation can be expressed as a function of e-folds

$$\begin{aligned} h_{int}=\frac{2M_\textrm{PL}}{\sqrt{3\xi }}\left[ \frac{\sqrt{3}}{2}+N_e \right] ^{1/2}. \end{aligned}$$

(9)

The constraint over the Higgs self coupling constant $\lambda$ and the non-minimal coupling constant $\xi$ can be obtained from the $\textrm{COBE}$ normalization $\frac{U}{\epsilon }=(0.027M_\textrm{PL})^4$ [53]. Plugging Eq. (9) into the $\textrm{COBE}$ normalization, we could express $\frac{\lambda }{\xi ^2}$ as a function of the number of e-folds. For $N_e=60$, the constrain on $\frac{\lambda }{\xi ^2}=4.41026\times 10^{-10}$. The inflationary parameters such as the scalar spectral index $n_s$ and the tensor-to-scalar ratio r are defined as $n_s=1-6\epsilon +2\eta$, $r=16\epsilon$. With the number of e-folds $N_e=60$ this model gives the values of r(0.0032) and $n_s$(0.9633),

which are well within the Planck bounds [86] of $n_s=0.9649\pm 0.0042$ and $r<0.10$ at 95$\%$ C.L.

During the slow-roll, scalar field perturbations are typically characterized in relation to the comoving curvature perturbation $\mathcal {R}$ and its power spectrum. The power spectrum of $\mathcal {R}$ is defined as [54]

$$\begin{aligned} \mathcal {P}_{\mathcal {R}}=\frac{1}{12\pi ^2}\frac{U^3(\phi )}{M_{PL}^6 U'^2(\phi )} , \end{aligned}$$

(10)

where $U'(\phi )$ is the derivative of $U(\phi )$ with respect to $\phi$ and both $U'(\phi )$ and $U(\phi )$ are calculated at $\phi _{int}$¹ corresponding to the beginning of inflation.

Fig. 1

Scalar power spectra $\mathcal {P}_{\mathcal {R}}$ as the function of the number of e-folds $N_e$ with different choices of $\lambda /\xi ^2$

In the presence of a dip in the scalar potential, the slow-roll conditions may not be valid (see Appendix D). A more precise determination of $\mathcal {P}_{\mathcal {R}}$ can be obtained by solving the Mukhanov–Sasaki equation, as given in Refs. [55,56,57,58,59].

The evolution of the scalar degrees of freedom, referred to as the curvature perturbation $\mathcal {R}$, is described by the following quadratic action

$$\begin{aligned} \mathcal {S}_2=\frac{1}{2}\int d\tau dx^3 z^2 [(\mathcal {R}')^2-(\partial \mathcal {R})^2] . \end{aligned}$$

(11)

Upon the change of the variable,

$$\begin{aligned} v=z\mathcal {R}~~~~~~\text {with}~~~~~~z=aM_{PL}\sqrt{2\epsilon _H}=a\frac{\dot{\phi }}{H}\,, \end{aligned}$$

(12)

it takes the form

$$\begin{aligned} \mathcal {S}_2[v]=\frac{1}{2}\int d\tau dx^3\left[ (v')^2-(\partial _iv)^2+\frac{z''}{z}v^2\right] . \end{aligned}$$

(13)

In this context, $(')$ denotes the derivative with respect to the conformal time $\tau =\int \frac{dt}{a(t)}$. The variable v, representing a scalar quantum field, is commonly known as the Mukhanov–Sasaki variable in the literature [57, 58]. The Fourier mode $v_k$ of v satisfies the well-known Mukhanov–Sasaki equation, expressed as:

$$\begin{aligned} v''_k+\left( k^2-\frac{z''}{z}\right) v_k=0, \end{aligned}$$

(14)

where the effective mass term is given by the following exact expression [60]

$$\begin{aligned} \frac{z''}{z}=(aH)^2 \left( 2-\epsilon _1+\frac{3}{2}\epsilon _2+\frac{1}{4}\epsilon _2^2-\frac{1}{2}\epsilon _1\epsilon _2+\frac{1}{2}\epsilon _2\epsilon _3\right) ,\nonumber \\ \end{aligned}$$

(15)

where $\epsilon _1=\epsilon _H$ and

$$\begin{aligned} \epsilon _{n+1}=-\frac{d \ln \,\epsilon _n}{dN_e} \end{aligned}$$

(16)

are the Hubble flow parameters. Given a mode k sufficiently early times when it is sub-Hubble i.e. $k \gg aH$ we can assume v to be in the Bunch–Davies vacuum [61] satisfying

$$\begin{aligned} v_k\rightarrow \frac{1}{\sqrt{2k}}e^{-ik\tau } . \end{aligned}$$

(17)

During inflation, as the comoving Hubble radius decreases, modes begin to enter the super-Hubble regime, i.e., $k \ll aH$. Equation (14) dictates that $|v_k|\propto z$, and consequently, $\mathcal {R}_k$ approaches a constant value. By solving the Mukhanov–Sasaki equation, we can estimate the dimensionless primordial power spectrum of $\mathcal {R}$ using the following relation²

$$\begin{aligned} \left. \mathcal {P_R}(k)=\frac{k^3}{2\pi ^2}|\mathcal {R}_k^2|~\right| _{k\ll aH}= \left. \frac{k^3}{2\pi ^2}\frac{ |v_k|^2 }{z^2}\right| _{k \ll aH} . \end{aligned}$$

(18)

The discrepancy of the scalar power spectrum under the slow-roll conditions and those obtained using Eq. (18) is illustrated in the lower panel of Fig. 8 in the Appendix D.

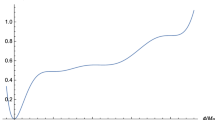
Recent CMB observations [62] suggested the value of $\mathcal {P}_{\mathcal {R}}=2.1\times 10^{-9}$ at the CMB pivot scale. Using Eqs. (10) and (9) we can express the power spectra as a function of the number of e-folds with different choices of $\lambda /\xi ^2$.

It is evident from Fig. 1 that $\mathcal {P}_{\mathcal {R}}$ attains a value of $2.1\times 10^{-9}$ at $N_e\sim 60$ e-folds with $\lambda /\xi ^2=10^{-10}$.

The concept of generating PBHs is examined within a class of single-field models of inflation. In this scenario, there is a notable contrast between the dynamics on small cosmological scales and the dynamics on large scales observed through the cosmic microwave background (CMB). This disparity proves advantageous in establishing the appropriate conditions for generating PBHs. Consequently, as the perturbed scales re-enter our Universe’s horizon during later stages of radiation and subsequent matter dominance, these initial seeds undergo collapse, leading to the formation of PBHs.

The generation of substantial scalar fluctuations during the inflationary period can lead to formation of significant density fluctuations, which play a vital role in the emergence of PBHs. The study of PBHs has garnered considerable attention over years, as PHBs have the potential to contribute a significant portion or even the entirety of the dark matter content of the Universe. However, the abundance of PBHs is subject to a number of stringent constraints imposed by their gravitational effects and evaporation rate. To produce PBHs in the early Universe, the magnitude of the curvature power spectrum needs to be approximately at the order of $10^{-3}$ to $10^{-2}$. In order to satisfy a successful inflation model, the curvature power spectrum is expected to yield a value of approximately $2.1 \times 10^{-9}$ at the scale of the CMB. Based on the information presented in Fig. 1, it is evident that the basic Higgs inflation model [37] lacks the ability to simultaneously address both the inflationary period and the production of PBHs. Several attempts have been made to address both scenarios, inflation and the production of PBHs, within the framework of Higgs Inflation. These attempts involve the introduction of new interactions to the Higgs field. By incorporating these additional interactions, it is possible to achieve a successful inflationary period while also generating the necessary conditions for production of PBHs [63,64,65,66,67,68,69,70].

3 Modified Higgs potential

This study examines a modified version of the Higgs potential that aims to address both the inflation and production of PBHs. Additionally, we investigate the implications of this modified potential in light of the recent NANOGrav signal [71]. Here we are adding a Gaussian dip (bump) [72] to the Higgs potential in Eq. (1). The structure of the Gaussian bump (dip) is given as follows³

$$\begin{aligned} \pm \Bigg [A e^{-\frac{(h(\phi )-h_0(\phi ))^2}{2 \sigma ^2}}\Bigg ] . \end{aligned}$$

(19)

After the conformal transformation, the potential transforms as

$$\begin{aligned} U_{eff}(\phi )=\frac{\lambda h^4(\phi )}{4} \frac{\left( 1\pm A e^{-\frac{(h(\phi )-h_0(\phi ))^2}{2 \sigma ^2}}\right) }{\left( \frac{h^2(\phi ) \xi }{M_{PL}^2}+1\right) ^2}. \end{aligned}$$

(20)

The Gaussian bump (dip) described in the above potential is featured by its height (depth) A and position $h_0$ and width $\sigma$. The potential can be expressed in terms of the redefined field $\phi$ using Eqs. (20) and (2). The slow roll parameters and the power spectrum for the modified Higgs potential are given in Appendix A. It is noteworthy that the incorporation of a dip in the inflaton potential leads to a violation of the slow-roll conditions [73,74,75] (see Appendix D).

3.1 Parameter space search

In order to investigate the appropriate parameter space of the power spectra $\mathcal {P}_{\mathcal {R}}[A,\sigma ,h_0,\lambda ,\xi ]$ that yields a value of $\mathcal {P}_{\mathcal {R}}=10^{-2}-10^{-3}$ for primordial black hole (PBH) formation and $\mathcal {P}_{\mathcal {R}}=2.1\times 10^{-9}$ for a successful inflation model at the cosmic microwave background (CMB) scale, we conduct a scan over the characteristics of the bump and dip. For this analysis, we fix the Higgs self-coupling constant at $\lambda =0.1$ and the Higgs gravity coupling at $\xi =10^4$.

Our parameter scans reveal that the addition of a dip feature to the potential produces a desired power spectrum for PBH formation in the early stages of inflation, as depicted in Fig. 2. On the other hand, the inclusion of a bump feature in the potential only results in the required power spectrum for PBH formation at late CMB scales (see Appendix B – Fig. 6).

Figure 2 illustrates the parameter space of $\sigma$ and $N_e$ with varying values of A and $h_0$. The red contour represents combinations of $\sigma$ and $N_e$ that yield $\mathcal {P}_{\mathcal {R}}=2.1\times 10^{-9}$ with fixed A and $h_0$. Meanwhile, the green contour represents $\mathcal {P}_{\mathcal {R}}=1\times 10^{-2}$. We consider a range of $\sigma$ from $10^{15}$ to $10^{18}$ GeV and choose four arbitrary values for the depth of the dip A (0.075, 0.1, 0.29, and 0.3). Similarly, we select four arbitrary values for the position of the dip $h_0$ ($1.76\times 10^{17}$ GeV, $1.8\times 10^{17}$ GeV, $2\times 10^{17}$ GeV, and $2.1\times 10^{17}$ GeV). For each combination we identify the corresponding values of $\sigma$ that yield the desired $\mathcal {P}_{\mathcal {R}}$ values for both inflation and PBH formation.

Fig. 2

The contour plot illustrates the permitted parameter space of $\sigma$ and $N_e$ for different choices of A and $h_0$ in the scenario of adding a dip structure, where the green contours correspond to $\mathcal {P}_{\mathcal {R}}=1\times 10^{-2}$ and the red contours correspond to $\mathcal {P}_{\mathcal {R}}=2.1\times 10^{-9}$

Figure 3 shows the scalar power spectra with the presence of a dip in the potential, which are calculated by solving the Mukhanov–Sasaki equation⁴ for the bench-mark points listed in Table 1. By observing Fig. 3 it becomes evident that certain parameter combinations can generate the correct power spectrum for both PBH formation and inflation at CMB scales. A comparison between Figs. 3 and 1 allows us to readily identify that the inclusion of a Gaussian dip in the potential has a significant impact on the power spectrum and enabling the formation of PHB seeds.

Fig. 3

The power spectra $\mathcal {P}_{\mathcal {R}}$ versus the number of e-folds $N_e$. Here the power spectra exhibit new characteristics as a result of the addition of a Gaussian dip in the Higgs potential

4 PBH formation

The PBH formation requires the power spectrum to be at least $\mathcal {O}(0.01)$, the power spectrum recorded in Fig. 3 guarantees this requirement. The power spectrum has an asymmetric peak with a dip structure at larger e-folds, and a comparison with the slow-roll approximation is shown in Appendix D. The curvature perturbation $\mathcal {R}_k$ is related to the density contrast by

$$\begin{aligned} \delta (t,k)=\frac{2(1+\omega )}{5+3\omega }\Big (\frac{k}{aH}\Big )^2\mathcal {R}_k . \end{aligned}$$

(21)

When the perturbations reenter the horizon in the radiation-dominated era, the over-dense region in the Universe (with $\delta >\delta _c$) would collapse into PBHs due to the increased amplification of curvature perturbations. This collapse occurs with $\omega =1/3$ and $\delta (t,k)=\frac{4}{9}\mathcal {R}_k$. Since the specifics of the PBH formation process are still unclear [76, 77], the precise value of the threshold $\delta _c$ remains uncertain. The original estimation of the critical density was first proposed by Bernard Carr in 1975 [5]. Carr demonstrated that overdensities collapse when the density contrast $\delta _c$ equals the square of the sound speed, denoted as $c_s^2$, with $c_s$ representing the sound speed. During the radiation-dominated epoch, the sound speed is equal to $1/\sqrt{3}$, resulting in $\delta _c=c_s^2=1/3$, which is equivalent to the parameter $\omega$. However, recent literature suggests a value of $\delta _c$ around 0.4. When the density fluctuation exceeds the critical density, overdense regions collapse and give rise to the formation of primordial black holes (PBHs).⁵

Table 1 Inflationary observables for the different choices of the potential parameters. The resulting PBH fraction $f_\textrm{PBH}$ of each region is indicated in Fig. 4. Here N is the number of e-folds, A, $h_0$, and $\sigma$ are the depth, the position, and the width of the dip, respectively. It is worth noting that the required peak and position (corresponding e-folds) of the power spectrum for the formation of primordial black holes are depicted in Fig. 3. The values of N shown in column 5 of Table 1 represent the number of e-folds at which the power spectrum curves of each region overlap with the Planck 18’ data. The values of $n_s$ and r, found in columns 6 and 7 of Table 1 respectively, are evaluated using the distinctive features of the dip at the number of e-folds presented in column 5 of Table 1. Note that the Planck 2018 results: $n_s = 0.9649 \pm 0.0042$ and $r < 0.10$ [86]

The critical density parameter is linked to the equation of state of the background by the following equation [79,80,81]:

$$\begin{aligned} \delta _c=\frac{3(1+\omega )}{5+3\omega }\text {sin}^2\Bigg ( \frac{\pi \sqrt{\omega }}{1+3\omega } \Bigg ) \end{aligned}$$

(22)

During the radiation-dominated epoch, when $\omega =1/3$, the critical density parameter can be calculated as $\delta _c=0.414$. It is important to note that Eq. (22) is not applicable during the matter-dominated epoch, characterized by $\omega =0$.

In the Press–Schechter formalism [82], the probability that the Gaussian density contrast, or alternatively, the Gaussian comoving curvature perturbations coarse-grained over the comoving Hubble scale by a suitable window function, is greater than the critical density $\delta _c$ for primordial black hole (PBH) formation is defined in terms of the mass fraction ($\beta (M)$) for a given mass M. This probability is expressed as follows:

Fig. 4

The fraction of PBHs as a dark matter candidate for the parameter sets: Region – a, b, c, d, e, and f in Table 1. The relevant observational constraints on the current primordial black hole (PBH) mass spectrum are represented by solid lines with shades. These constraints include extra-galactic gamma-ray (EG$\gamma$) observations [89], Subaru HSC microlensing (HSC) results [90], Kepler milli/microlensing (Kepler) measurements [91], EROS/MACHO microlensing observations (EROS/MACHO) [92], dynamical heating of ultra-faint dwarf galaxies (UFD) [93], constraints from X-ray/radio observations [94], and the accretion constraints by CMB [95,96,97]

$$\begin{aligned} \beta (M_{PBH})= & 2\gamma \int _{\delta _c}^\infty \frac{d\delta }{\sqrt{2\pi }\sigma _{MPH}}exp\Big (-\frac{\delta ^2}{2\sigma ^2_{PBH}}\Big )\nonumber \\\simeq & \sqrt{\frac{2}{\pi }}\frac{\gamma }{\nu _c}exp\Big (-\frac{\nu ^2_c}{2}\Big ), \end{aligned}$$

(23)

where $\gamma$ is the fraction of mass transformed to be PBHs that has $\delta >\delta _c$, and in this study, we choose $\gamma =0.4$ [63, 83,84,85]. Here $\nu _c=\delta _c/\sigma _{M_{PBH}}$ and the variance $\sigma _{M_{PBH}}$ is defined as

$$\begin{aligned} \sigma ^2_{M_{PBH}}=\int _0^\infty \frac{dk}{k}\frac{16}{81}(kR)^4 W^2(kR)\mathcal {P}_{R}(k) , \end{aligned}$$

(24)

where W(kR) is the window used to smooth the density contrast on comoving scale R. We use the Gaussian-type window function in this work,

$$\begin{aligned} W(kR)=\exp \left( -\frac{k^2R^2}{2}\right) . \end{aligned}$$

(25)

The mass fraction is ultimately determined or obtained by performing the necessary calculations or calculations based on the assumptions and considerations mentioned earlier [87, 88].

$$\begin{aligned} \beta (M_{PBH})=\gamma \sqrt{\frac{2}{\pi }}~\frac{4\mathcal {P}_{R}(k)}{9\delta _c}exp\left( -\frac{81\delta ^2_c}{32\mathcal {P}_{R}(k)}\right) . \end{aligned}$$

(26)

The mass fraction of PBHs can be related to the abundance $f_{PBH}$ as follows when considering PBHs as a fraction of dark matter:

$$\begin{aligned} \beta (M_{PBH})= & 3.7\times 10^{-9}\Big (\frac{\gamma }{0.2}\Big )^{-1/2}\nonumber \\ & \times \Big (\frac{g_{*form}}{10.75}\Big )^{1/4}\Big (\frac{M_{PBH}}{M_{\odot }}\Big )^{1/2}f_{PBH}, \end{aligned}$$

(27)

where $M_{\odot }$ is the solar mass and $g_{*form}$ is the relativistic degrees of freedom at formation.

The mass of PBH at the formation can be written as a fraction of horizon mass given by

$$\begin{aligned} M_{PBH}= & 1.36\times 10^{18}\left( \frac{\gamma }{0.2}\right) \left( \frac{g*}{106.75}\right) ^{-1/6}\nonumber \\ & \times \left( \frac{k}{7\times 10^{13}~ Mpc^{-1}}\right) ^{-2} \end{aligned}$$

(28)

where $k=k_{*}e^{N-N_e}$, the “*” denotes the CMB pivot scale, $N_e$ is the number of efolds at the beginning of the inflation. One can calculate the mass fraction of PBHs using Eqs. ((26)–(28)).

We obtain the abundance of PBHs as dark matter, denoted as $f_{PBH}$, for a critical threshold parameter $\delta _c=0.414$ [83]. The corresponding results are presented in Fig. 4. Information regarding the distinct regions marked in Fig. 4 can be found in Table 1. A dip is observed with a depth of $A=0.29$ and 0.3, accompanied by widths of $\sigma =1.31\times 10^{17}$ GeV and $1.40\times 10^{17}$ GeV, and positioned at $h_0=1.76\times 10^{17}$ GeV and $1.8\times 10^{17}$ GeV. This setting generates PBHs that potentially contribute to almost $100\%$ of the dark matter, as indicated by the regions labeled a and b in Fig. 4.

The parameters associated with regions a, b c, d, e, and f produce PBHs and spectral index $n_s$

situated within $3\sigma$ of (except for point d, which deviates by $3.9\sigma$ on $n_s$) cosmic microwave background (CMB) observations.

Moreover, these parameters have the capability to generate heavier PBHs. In our study, we conducted several parameter space scans to generate PBHs. One common feature that emerged was an increase in the depth A of the potential, resulting in the production of lighter PBHs while keeping other parameters fixed. For instance, in Table 1, we observe this behavior in the case of region b and c, where $h_0$ remains fixed and A ranges from 0.1 to 0.3. Similarly, decreasing the value of $h_0$ while keeping other parameters fixed leads to a transition that yields lighter PBHs. This is exemplified by the behavior of region d and b in Table 1, where A is fixed and $h_0$ varies from $2\times 10^{17}$ GeV to $1.8\times 10^{17}$ GeV.

Another noteworthy feature of the dip is that fixing both the depth A and position $h_0$ to specific values while increasing the width $\sigma$ of the dip, would result in a reduction and eventual disappearance of the $f_{PBH}$ curve. Higher values of $\sigma$ indicate the absence of a dip, with the potential reverting to its original form and no dip effect. We have demonstrated this behavior in Appendix C, where we fixed $A=0.3$ and $h_0=1.8\times 10^{17}$ GeV and progressively increased the width $\sigma$.

5 Stochastic second-order gravitational wave background

Production of gravitational waves through the second-order effect occurs simultaneously with the formation of PBHs, specifically when the modes re-enter the Hubble radius. Following their production, the gravitational waves propagate freely during subsequent epochs of the Universe due to their low interaction rates. The frequency of these gravitational waves corresponds to the Hubble mass at that particular time. Considering that the mass of PBHs is proportional to the Hubble mass, we can establish a relationship between the PBH mass and the present-day frequency of gravitational waves [98].

$$\begin{aligned} f_{GW}\simeq 10^{-9}\Big (\frac{M_{PBH}}{30M_{\odot }}\Big )^{-\frac{1}{2}}~\text {Hz}. \end{aligned}$$

(29)

The large density perturbations not only produce the PBH dark matter but also generate the second-order gravitational wave signal [99, 100]. In linear perturbation theory, there is a distinct separation between tensor and scalar perturbations, and they evolve independently. However, when considering perturbations at the second order, this separation no longer holds true. The generation of gravitational waves resulting from the initial scalar perturbations arises due to their interplay and coupling at the second order. The perturbed metric can be decomposed as [101]

$$\begin{aligned} g_{\alpha \beta }=\bar{g}_{\alpha \beta }+\delta g_{\alpha \beta }+\delta ^2 g_{\alpha \beta } . \end{aligned}$$

(30)

The metric components are defined as follows: $\bar{g}_{\alpha \beta }$ represents the background FLRW metric, $\delta g_{\alpha \beta }$ exclusively contains scalar degrees of freedom, and $\delta ^2 g_{\alpha \beta }$ generally encompasses scalar, vector, and tensor modes induced by $\delta g_{\alpha \beta }$. However, since our focus is solely on the induced tensor modes, we neglect any scalar and vector modes at the second order. Consequently, we express the perturbed metric as follows [98]:

$$\begin{aligned} ds^2= & a^2(\tau )\Bigg [-(1+\Phi )d\tau ^2\nonumber \\ & + \Big [(1-2\Psi )\delta _{ij}+\frac{1}{2}h_{ij}\Big ]dx^i dx^j \Bigg ] . \end{aligned}$$

(31)

In this context, the symbols $\Phi$ and $\Psi$ denote the Bardeen potentials, which characterize first-order scalar perturbations, as described in Ref. [102]. It is worth noting that in the absence of anisotropic stress, these potentials are equal, i.e., $\Phi = \Psi$. On the other hand, we use the notation $h_{ij}$ to represent the second-order tensor perturbations that are induced. It is important to emphasize that these tensor perturbations possess traceless and transverse characteristics, meaning that they satisfy $\partial _i h_{ij} = 0$ and $h^i_{i}=0$

The Fourier transform of $h_{ij}$ can written as[7],

$$\begin{aligned} h_{ij}({\textbf {x}},\tau )= & \frac{1}{(2\pi )^{3/2}}\int d^3k e^{i{\textbf {k.x}}}\nonumber \\ & \times \Big [h^{+}({\textbf {k}},\tau )q^+_{ij}({\textbf {k}}) + h^{\times }({\textbf {k}},\tau )q^\times _{ij}({\textbf {k}}) \Big ] , \end{aligned}$$

(32)

where $q^+_{ij}$ and $q^\times _{ij}$ denote the polarization tensors that have non-zero components in the plane perpendicular to the direction of the propagation and are expressed in terms of orthonormal basis vectors $\textbf{e}$ and $\bar{\textbf{e}}$ orthogonal to $\textbf{k}$:

$$\begin{aligned} q^+_{ij}=\frac{1}{\sqrt{2}}\Big [ e_i({\textbf {k}})e_j({\textbf {k}}) - \bar{e}_i({\textbf {k}})\bar{e}_j({\textbf {k}}) \Big ] \end{aligned}$$

(33)

$$\begin{aligned} q^\times _{ij}=\frac{1}{\sqrt{2}}\Big [ e_i({\textbf {k}})\bar{e}_j({\textbf {k}}) + \bar{e}_i({\textbf {k}})e_j({\textbf {k}}) \Big ] , \end{aligned}$$

(34)

in which orthonormality leads to the normalization condition: $q_{ij}^\lambda ({\textbf {k}})q^{\lambda ',ij}=\delta ^{\lambda \lambda '}$, where $\lambda$ and $\lambda '$ can be either $+$ or $\times$

Fig. 5

The gravitational wave abundance $\Omega _\textrm{GW} h^2$ versus the frequency f, corresponding to the benchmark parameter sets listed in Table 1. They are compared with the recent NANOGrav 15 years sensitivity [71] (black curve) and projecting SKA/THEIA [110, 111], which utilize the observations of pulsar timing array for stochastic GW of $\mathcal {O}(\textrm{nHz})$. The planned GW interferometers LISA/$\mu$Ares [112,113,114] will cover the range from $\mu$Hz to Hz. Region f is zoomed in at the bottom of the figure

The modes we are concerned with return within the Hubble radius during the radiation-dominated era. To describe the dynamics of these Fourier modes, we can derive their equations of motion by applying second-order perturbations to the Einstein equations, which account for the induced tensor perturbation, $h_{ij}$. Additionally, we utilize the Bardeen equation, a differential equation describing scalar perturbations, when $\Phi = \Psi$. In the context of radiation domination and in Fourier space, the amplitude of the tensor mode, for each polarization, is governed by the following equation [101]:

$$\begin{aligned} \frac{d^2h(\textbf{k},\tau )}{d\tau ^2}+\frac{2}{\tau }\frac{dh(\textbf{k},\tau )}{d\tau }+k^2h(\mathbf {(}k),\tau )=\mathcal {S}(\mathbf {(}k),\tau ), \end{aligned}$$

(35)

where the source term $\mathcal {S}$ is [103, 105]

$$\begin{aligned} \mathcal {S}&= \int \frac{d^3\widetilde{k}}{(2\pi )^{3/2}}\widetilde{k}^2 \Bigg [1-\Bigg (\frac{\textbf{k}\cdot \textbf{k}}{k \widetilde{k}}\Bigg )^2 \Bigg ]\times \Bigg (12\Phi (\textbf{k}-\mathbf {\widetilde{k}},\tau )\Phi (\mathbf {\widetilde{k}},\tau ) \nonumber \\&\quad + 8\Bigg [\tau \Phi (\textbf{k}-\mathbf {\widetilde{k}},\tau )+\frac{\tau ^2}{2} \frac{d\Phi (\textbf{k}-\mathbf {\widetilde{k}},\tau )}{d\tau } \Bigg ] \frac{d\Phi (\textbf{k}-\mathbf {\widetilde{k}},\tau )}{d\tau } \Bigg ), \end{aligned}$$

(36)

where the Bardeen potential $\Phi =\frac{2\mathcal {R}}{3}$ satisfy the equation [103, 105]

$$\begin{aligned} \frac{d^2\Phi }{d\tau ^2}+\frac{4}{\tau }\frac{d\Phi }{d\tau }+\frac{1}{3}k^2\Phi =0 \end{aligned}$$

(37)

Utilizing the Green function method to solve Eq. (35) yields the present relative energy density attributed to gravitational waves [103,104,105,106,107,108]:

$$\begin{aligned} & \Omega _{GW}=c_g\frac{\Omega _{r,0}}{6}\int _0^\infty dv \int _{|1-v|}^{1+v}du\nonumber \\ & \Bigg ( \frac{4v^2-(1+v^2-u^2)^2}{4uv}\Bigg )^2 \overline{\mathcal {I}^2(u,v)}\mathcal {P_R}(kv)\mathcal {P_R}(ku), \end{aligned}$$

(38)

where $\Omega _{r,0}\sim 5.38\times 10^{-5}$ is the current radiation energy density fraction [109], $x=k\tau$ with $\tau$ being the conformal time, $c_g=\frac{a_f^4\rho _r(\tau _f)}{\rho _r(\tau _0)}=\frac{g_*}{g_*^0}(\frac{g_{*S}^0}{g_{*S}})^{4/3}\sim 0.4$ by taking the current universe effective energy and entropy degree of freedom as $g_{*}^0=3.36$ and $g^0_{*S}=3.91$, respectively. The degree of freedom at the evaluation of perturbations take the value $g_*=g_{*S}=106.75$. $\overline{\mathcal {I}^2(u,v)}$ is expressed as [106,107,108]:

$$\begin{aligned} \overline{\mathcal {I}^2(u,v)}&= \frac{1}{2}\Bigg [\frac{3(u^2+v^2-3)}{4u^3v^3}\Bigg ]^2\nonumber \\&\quad \times \Bigg [\Bigg (-4uv+(u^2+v^2-3)\ln \Bigg |\frac{3-(u+v)^2}{3-(u-v)^2}\Bigg |\Bigg )^2\nonumber \\&\quad + \pi ^2(u^2+v^2-3)^2\Theta (v+u-\sqrt{3})\Bigg ] \end{aligned}$$

(39)

In the main plot (Fig. 5), our results indicate the values of $\Omega _{GW}h^2$, where $h=\frac{H_0}{100\,km/s/Mpc}$, $H_0=67.27\,\textrm{km}/s$, and which are divided into several distinct regions. Each region is denoted and explained in Table 1.

Region f, depicted in Fig. 5, is particularly relevant as it can potentially explain the recent findings from NANOGrav [71]. The parameter space associated with region f is characterized by a dip in the Higgs potential with a depth of $A=0.075$ and a width of $7.83\times 10^{16}$ GeV. This dip is positioned at $h_0=2.1\times 10^{17}$ GeV.

The relationship expressed in Eq. (29) reveals that $f_{GW}$ is proportional to $(M_{PBH})^{-1/2}$, indicating an inverse dependence between the frequency of gravitational waves ($f_{GW}$) and the mass of primordial black holes ($M_{PBH}$).

Additionally, it is worth noting that increasing the depth A and shifting the position $h_0$ of the dip in the Higgs potential can lead to a shift in the corresponding curves towards higher frequency regimes. This observation suggests that adjustments in the parameters controlling the dip can influence the frequency spectrum of the generated gravitational waves.

6 Conclusions

In this study, we have investigated possible modifications to the classical Higgs inflation model proposed by M. Shaposhnikov and F. L. Bezrukov. We have introduced a modification to the Higgs potential by incorporating a dip at the top base of the potential. This modification has a significant impact on the generation of curvature perturbations, resulting in the amplification of second-order stochastic gravitational wave production and potential formation of PBHs. These effects were absent in the classical model. Note that the scalar potential with a highly peaked or dipped spectrum may suffer from large one-loop correction [116], unless some mechanisms are introduced to avoid the quadratic divergence, such as supersymmetry.

To our knowledge we have not found a realistic UV model that concretely generates a bump/dip in the inflaton potential. One of the early papers [72] only mentioned that such a bump-like feature can be generated by a small local radiative correction to the base potential. The closest UV semi-realistic model to realize the effective potential with a dip structure is to supplement the Higgs inflation with a TeV scale dark matter (DM) candidate and a heavy right-handed neutrino [117, 118]. In the Jordan frame, the renormalization-group running of the Higgs quartic coupling $\lambda (\mu )$ can be made positive up to $M_\textrm{Pl}$ due to the radiative corrections of the DM. On the other hand, the contribution from the right-handed neutrino pulls down $\lambda (\mu )$, such that $\lambda (\mu )$ induces a minimal value near the Planck scale. After conformal transformation, the effective potential behaves exponentially flat with a dip-like structure, which corresponds to the location of the local minimal $\lambda (\mu )$. Nevertheless, we have adopted a phenomenological approach for a bump/dip in our work.

There are other types of models, including inflection points and steps in the base potential, that can slow down the rolling of the inflaton (similar to the bump/dip) such that it enters the ultra-slow roll phase and generates a $10^7$ enhancement in the curvature power spectrum for the formation of the primordial black hole. One example of inflection-point inflation is given by an extra $R^2$ term in the modified Higgs inflation model with non-minimal coupling in Ref. [66]. It induced a near-inflection point. There is another example using the axion field to generate bumpy potential [119], in which it may be possible to have superimposition of various axion fields to generate a single bump/dip.

Although these types of models appear to be different, they share some common properties for the feature (dip/bump, inflection point, or step). (i) The position $h_0$ of the feature in the inflaton field space determines the PBH mass. (ii) The height and the width of the feature of the bump/dip, step, or inflection point determine how slow the inflaton rolls, which determines the magnitude of the curvature power spectrum and the PBH abundance. In literature, the model of inflection-point inflation involves higher-order terms of the field in the potential, which is regarded as an effective theory, instead of a realistic UV model. Not to mention the steps in the inflaton potential, which is more phenomenological. It is still worth the efforts to study the effect of the bump/dip.

The introduction of the dip in the potential leads to an enhancement in the power spectrum, which in turn allows for the potential existence of PBHs with masses ranging from $1.5\times 10^{20}$ g to $9.72\times 10^{32}$ g, depending on the chosen parameter space. Additionally, we have demonstrated that the selected parameter values for PBH production align with the allowed values for inflationary parameters. This suggests a consistent and viable framework for understanding the origins of PBHs and their role as potential contributors to the dark matter content of our universe.

Furthermore, we have identified specific regions within the parameter space that could account for a significant portion of the observed dark matter. By considering various cosmological constraints, we have established the consistency of these parameter regions. Additionally, we found that the resulting gravitational wave signals from our model can explain the observed excess observed by NANOGrav.

In conclusion, our study highlights the importance of the modified Higgs potential in the context of the classical Higgs inflation model. The introduced dip within the potential enhances the power spectrum. It is crucial to emphasize that the parameter spaces governing region (f), aimed at potentially elucidating the NANOGrav signal, and regions (a) and (b), accountable for a substantial portion of dark matter in the form of primordial black holes (PBHs), exhibit clear disparities. Consequently, the model may hold promise in addressing at least one of these phenomena.

Appendices

Appendix A: Slow slow roll parameters and power spectrum for the modified Higgs potential under slow roll approximation

The slow-roll and other inflationary parameters with this effective potential (Eq. 20) can be expressed as by following Eqs. (5)–(10),

$$\begin{aligned} \epsilon =\frac{\left( A \text {Mpl}^2 \left( h \left( h^2-4 \sigma ^2\right) \pm h^2 h_0\right) +A h^4 \xi \left( h\pm h_0\right) +4 h \text {Mpl}^2 \sigma ^2 e^{\frac{\left( h- h_0\right) ^2}{2 \sigma ^2}}\right) ^2}{12 h^6 \xi ^2 \sigma ^4 \left( A\pm e^{\frac{\left( h-h_0\right) ^2}{2 \sigma ^2}}\right) ^2} \end{aligned}$$

(A1)

Using $\epsilon =1$, we can obtain the Higgs field value at the end of inflation.

$$\begin{aligned} \begin{aligned} \eta&= \frac{\pm A \left( h^6 \xi \left( 2 \left( h-2 h_0\right) \text {Mpl}^2+\xi \left( -2 h \sigma ^2+h h_0^2+h_0 \sigma ^2\right) \right) \right. }{6 h^4 h \xi ^2 \sigma ^4 \left( e^{\frac{\left( h-h_0\right) ^2}{2 \sigma ^2}}\pm A\right) } \\&\quad + \frac{\left. h^4 \text {Mpl}^2 \left( \left( h-2 h_0\right) \text {Mpl}^2+2 \xi \left( -5 h \sigma ^2+h h_0^2+4 h_0 \sigma ^2\right) \right) \right. }{6 h^4 h \xi ^2 \sigma ^4 \left( e^{\frac{\left( h-h_0\right) ^2}{2 \sigma ^2}}\pm A\right) } \\&\quad + \frac{\left. h \text {Mpl}^2 \left( h^2 \left( h_0^2 \text {Mpl}^2-8 \sigma ^2 \left( \text {Mpl}^2+\xi \sigma ^2\right) \right) +8 \text {Mpl}^2 \sigma ^4\right) \right. }{6 h^4 h \xi ^2 \sigma ^4 \left( e^{\frac{\left( h-h_0\right) ^2}{2 \sigma ^2}}\pm A\right) } \\&\quad + \frac{\left. 7 h_0 h^2 \text {Mpl}^4 \sigma ^2 + \left( h-2 h_0\right) h^8 \xi ^2\right) - 8 h \text {Mpl}^2 \sigma ^4 e^{\frac{\left( h-h_0\right) ^2}{2 \sigma ^2}} \left( h^2 \xi -\text {Mpl}^2\right) }{6 h^4 h \xi ^2 \sigma ^4 \left( e^{\frac{\left( h-h_0\right) ^2}{2 \sigma ^2}}\pm A\right) } \end{aligned}\nonumber \\ \end{aligned}$$

(A2)

The number of e-folds for each case is calculated as

$$\begin{aligned} N_e=6 \xi ^2 \int _{h_{end}}^{h_{int}} \frac{h^3}{\left( h^2 \xi +\text {Mpl}^2\right) ^2 \left( \frac{A \left( h^2\pm h h_0\right) }{\sigma ^2 \left( e^{\frac{\left( h-h_0\right) ^2}{2 \sigma ^2}}\pm A\right) }+\frac{4 \text {Mpl}^2}{h^2 \xi +\text {Mpl}^2}\right) } \, dh\nonumber \\ \end{aligned}$$

(A3)

The ± signs in Eqs. (A1)–(A3) represents the bump and dip, respectively. Compared to the original model of inflation, the new modification generates complex values for $\epsilon ,\eta , ~\text {and}~ N_e$. The analytical evaluation of these quantities is harder, and it is not possible to solve the Eq. (A3) analytically, so we employ a numerical approach to compute the inflationary observables. The calculations of these observables, as well as the analysis of PBHs, are performed using a Python code developed by the authors. The power spectra are obtained as

$$\begin{aligned} \mathcal {P}_{\mathcal {R}} = {\left\{ \begin{array}{ll} \frac{h^8 \lambda \xi ^2 \sigma ^4 e^{-\frac{\left( h-h_0\right) ^2}{2 \sigma ^2}} \left( A+e^{\frac{\left( h-h_0\right) ^2}{2 \sigma ^2}}\right) ^3}{8 \pi ^2 \left( h^2 \xi +\text {Mpl}^2\right) ^2 \left( A \left( h h_0 \left( h^2 \xi +\text {Mpl}^2\right) -h^2 \text {Mpl}^2+h^4 (-\xi )+4 \text {Mpl}^2 \sigma ^2\right) +4 \text {Mpl}^2 \sigma ^2 e^{\frac{\left( h-h_0\right) ^2}{2 \sigma ^2}}\right) ^2}, & \text {Potential with bump} \\ \frac{h^8 \lambda \xi ^2 \sigma ^4 e^{-\frac{\left( h-h_0\right) ^2}{2 \sigma ^2}} \left( e^{\frac{\left( h-h_0\right) ^2}{2 \sigma ^2}}-A\right) ^3}{8 \pi ^2 \left( h^2 \xi +\text {Mpl}^2\right) ^2 \left( A \left( -h h_0 \left( h^2 \xi +\text {Mpl}^2\right) +h^2 \text {Mpl}^2+h^4 \xi -4 \text {Mpl}^2 \sigma ^2\right) +4 \text {Mpl}^2 \sigma ^2 e^{\frac{\left( h-h_0\right) ^2}{2 \sigma ^2}}\right) ^2}, & \text {Potential with dip} \end{array}\right. } \end{aligned}$$

(A4)

The new power spectrum is characterized by 5 parameters $[A,\sigma ,h_0,\lambda ,\xi ]$. By tuning these variables we can obtain the proper parameter space for the inflation, PBH production, and stochastic gravitational wave background (SGWB).

Appendix B: Bump parameter space

The addition of a Gaussian bump to the Higgs Inflation model can indeed amplify the power spectra. However, such enhancements are only observed within a specific region characterized by a large number of e-folds. For PBH formation to occur, the inflationary power spectrum needs to be enhanced by a factor of $10^7$ within fewer than 40 e-folds of expansion.

Fig. 6

The contour plot illustrates the permitted parameter space of $\sigma$ and $N_e$ for different choices of A and $h_0$ in the scenario of adding a bump structure, where the green contours correspond to $\mathcal {P}_{\mathcal {R}}=1\times 10^{-2}$ and the red contours correspond to $\mathcal {P}_{\mathcal {R}}=2.1\times 10^{-9}$

Fig. 7

The corresponding PBH abundance for the benchmark parameter $A=0.3,~h_0=1.8\times 10^{17}~\textrm{GeV}$ with the increment of the width $\sigma$ of the dip in the Higgs potential

By comparing Fig. 2 with Fig. 6, it becomes evident that the current bump on the potential does not provide an adequate parameter space for PBH formation. In Fig. 6 we have shown some examples of such behavior, We explore a specific parameter space characterized by a bump with a height of $A=0.1$ (or 0.3) and positioned at $1.8\times 10^{17}$ GeV (or $2\times 10^{17}$ GeV). By scanning the values of $\sigma$ and $N_e$, we generate the necessary power spectra for PBH formation. It is observed that these parameter combinations are effective for generating PBHs during later and heavier epochs of inflation, as illustrated in Fig. 6. Conversely, when a similar set of values is used with a dip feature in the potential, it facilitates PBH formation during smaller e-folding periods.

Fig. 8

The corresponding slow-roll parameters and power spectra for the benchmark point $A=0.1,~h_0=2\times 10^{17}~\textrm{GeV}, \sigma =8.45\times 10^{16}$ GeV of the dip in the Higgs potential

Appendix C: PBH abundance vs $\sigma$ values

In this section, we demonstrate, using Fig. 7, that when both the depth A and position $h_0$ of the dip in the potential are fixed at specific values, increasing the width $\sigma$ leads to a reduction and eventual disappearance of the $f_{PBH}$ curve. Higher values of $\sigma$ indicate the absence of a dip, causing the potential to revert to its original form without a dip effect. Specifically, we set $A=0.3$ and $h_0=1.8\times 10^{17}$ GeV to illustrate this feature. It is important to note that this behavior can also be observed with other choices of A and $h_0$.

Appendix D: Inflation and power spectra

In order to support the inflationary process, it is essential for the scalar field $\phi$ to undergo a gradual descent along its potential, ensuring that the potential energy prevails over kinetic energy. Furthermore, for a prolonged period of inflation, it is imperative that the acceleration of the inflaton field remains negligible. These conditions, known as slow-roll conditions, are characterized by two slow-roll parameters denoted as $\epsilon _H$ and $\eta _H$

$$\begin{aligned} \epsilon _H=-\frac{\dot{H}}{H^2}=\frac{1}{2M_p^2}\frac{\dot{\phi }}{H^2}, \end{aligned}$$

(D1)

$$\begin{aligned} \eta _H= -\frac{\ddot{\phi }}{H\dot{\phi }}=\epsilon _H+\frac{1}{2\epsilon _H}\frac{d\epsilon _H}{dN_e} \end{aligned}$$

(D2)

Under the slow-roll approximation, Eqs. (D1) and (D2) can be simplified to Eqs. (5) and (6). The incorporation of a dip in the inflaton potential leads to a violation of the slow-roll conditions. We computed the slow-roll parameters using the expansion formulas provided in [115], as illustrated in the upper panel of Fig.  8 along with a benchmark point. The figure unmistakably indicates a clear instance of slow-roll violation in the region where a peak in the power spectra is observed due to the introduction of a dip in the potential.

The lower panel in Fig. 8 compares the corresponding scalar power spectrum $\mathcal{P_R}$ using the exact and the slow-roll approximated formulas. It is clear that they have some differences.