Systematic Elastostatic Stiffness Model of Over-Constrained Parallel Manipulators Without Additional Constraint Equations

Abstract

The establishment of an elastostatic stiffness model for over constrained parallel manipulators (PMs), particularly those with over constrained subclosed loops, poses a challenge while ensuring numerical stability. This study addresses this issue by proposing a systematic elastostatic stiffness model based on matrix structural analysis (MSA) and independent displacement coordinates (IDCs) extraction techniques. To begin, the closed-loop PM is transformed into an open-loop PM by eliminating constraints. A subassembly element is then introduced, which considers the flexibility of both rods and joints. This approach helps circumvent the numerical instability typically encountered with traditional constraint equations. The IDCs and analytical constraint equations of nodes constrained by various joints are summarized in the appendix, utilizing multipoint constraint theory and singularity analysis, all unified within a single coordinate frame. Subsequently, the open-loop mechanism is efficiently closed by referencing the constraint equations presented in the appendix, alongside its elastostatic model. The proposed method proves to be both modeling and computationally efficient due to the comprehensive summary of the constraint equations in the Appendix, eliminating the need for additional equations. An example utilizing an over constrained subclosed loops demonstrate the application of the proposed method. In conclusion, the model proposed in this study enriches the theory of elastostatic stiffness modeling of PMs and provides an effective solution for stiffness modeling challenges they present.

1 Introduction

Elastostatic analysis is an important engineering task. Through static analysis, the stiffness and strength of the parallel manipulators (PMs) can be evaluated, providing essential data to support the rationality of mechanism design. However, establishing the complex constraint equations for multi-joint and multi-object systems, particularly over constrained PMs with over constrained subclosed loops, remains a challenging task [1,2,3,4], establishing their complex constraint equations has always been a challenging task. Currently, the primary methods for elastostatic analysis of such methods include the virtual joint method (VJM) [5], screw theory [6], and matrix structure analysis (MSA) [7].

The VJM simulates the elastic beam element by representing it as a rigid beam supported by a centralized springs [8] at both. This approach, however, overlooks the continuum nature of the beam element [9]. The VJM considers the elasticity of a joint by establishing a static equation based on the constraint reactions and deformation differences at the constrained nodes [10]. However, when the joint is assumed to be rigid, the static equation can become singular [11]. In addition, the VJMs do not establish a comprehensive method for addressing the complex constraint relationships inherent in the mechanism.

The screw theory method [12] addresses the constraint conditions of a mechanism by utilizing the principle that the reciprocal product of the twist and constraint wrenches is zero [13]. This method does not require additional constraint equations and is characterized by its clear physical significance. First, the screw theory method establishes the constrained wrench system of the mechanism based on the structural constraint relations. Subsequently, the limb stiffness matrix of the structure is established. Finally, the overall stiffness matrix of the structure is determined using the virtual work principle. Xu et al. [14] developed a compact stiffness matrix for a limb by integrating the basic deformation principle with two mappings in the direction of the constrained wrench system. Hu et al. [15] established an extended-limb stiffness matrix based on the basic deformation principle. Yang et al. [16] developed a compact limb stiffness matrix using strain energy and Castigliano’s second theorem. However, the application of screw theory to over constrained PMs with over constrained closed loops has been scarcely reported. Moreover, screw theory poses challenges for coding, making it difficult to generalize in engineering applications.

MSA technology establishes an expanded static structural model through element coding [17, 18] and then combines constraint equations to establish an elastostatic stiffness model. Notable examples include the work of Klimchik et al. and Deblaise et al. [19, 20]. Klimchik et al. [19] detailed the basic theory of MSA and linear displacement boundary conditions but did not establish an angular displacement deformation coordination equation in the global coordinate system. Deblaise et al. [20] established the boundary conditions of the mechanism based on the principle of minimum potential energy and then developed a static model of the delta mechanism. In these studies, the elastic joint was regarded as an independent element [21] to establish the deformation coordination equation. To avoid numerical instability, the stiffness of the joint in the direction of free motion was set to a value close to zero rather than zero, which deviates from the theoretical analysis. MSA assembles the elements of the free body through deformation coordination equations to establish the overall elastostatic stiffness model, making it ideal for coding and engineering applications. However, these studies did not extract the independent angular displacement coordinates of the mechanism within a unified coordinate system, nor did they consider the actual stiffness matrix of the elastic joint.

This study proposes a systematic elastostatic stiffness model for PMs based on MSA technology, with two main contributions. First, a subassembly element stiffness matrix including beam and elastic joint elements is proposed. This matrix accounts for the actual stiffness of the elastic joints and avoids the numerical instability typically associated with the constraint equations. Second, the independent linear/angular displacement coordinates of the constraint nodes connected by various joints are extracted with a unified global coordinate system. This approach enables the rapid assembly of the elastostatic stiffness model of the PMs without the need for additional constraint equations. The proposed model is beneficial for coding and engineering applications. The principle of the stiffness model proposed in this study is to assemble the overall stiffness matrix of the mechanism based on the constraint characteristics of the joints. Consequently, the proposed model is universal, making it applicable to both non-over constrained and complex over constrained PMs.

This paper is divided into four sections to describe the proposed method. Section 2 introduces the elastostatic stiffness model proposed in this study. This section covers the sub-assembly element stiffness matrix, independent displacement coordinates (IDCs) of boundary nodes connected by various joints, and the overall PM model. Section 3 demonstrates the superiority of the sub-assembly element using a simple single-freedom structure as an example. Section 4 applies the proposed method to an over constrained PM with over constrained subclosed loops, displaying implementation of method. Finally, conclusions are presented in Section 5.

2 Elastostatic Stiffness Model of PMs

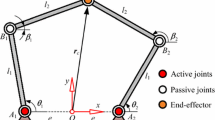
A general PM is shown in Figure 1. The moving platform is connected to the fixed base by n limbs, and each limb consists of m_i links. To better illustrate the modeling method proposed in this work, the following assumptions were made. The base, moving platform, and actuators were assumed to be rigid; the friction and clearance of the joints were ignored [22, 23], and the flexibility of the rods and joints was considered.

Figure 1

A general PM: (a) Closed-loops, (b) Open-loops

The procedure of the proposed elastostatic stiffness model is illustrated as follows: (1) Convert the closed-loop PM into an open loop by cutting the joints, considering the rod and joints as subassembly bodies, and formulate their element stiffness matrix and non-independent general displacement coordinates; (2) Extract the IDCs of boundary nodes connected by joints using MPC theory and establish the global IDCs; (3) Close the open loops by establishing the mapping relationship from the non-independent displacement coordinates of each free body to the global IDCs and establish the elastostatic stiffness model of PMs through MSA technology.

A schematic of the proposed model is shown in Figure 2. To establish an overall stiffness model that accurately represents the exit node of the mechanism, two key issues must be addressed. One is to establish the subassembly element stiffness matrix, and the other is to extract the global IDCs and establish mapping matrices from the displacement column vector of the free body to the global IDCs.

Figure 2

The schematic diagram of the proposed stiffness modeling based on the MSA

2.1 Subassembly Element Stiffness Matrix

In engineering, elastic rods are often connected through elastic joints, posing a challenging task in handling these constraints and often leading to unstable numerical calculations. In this study, the elastic rod and joints connected at both ends were innovatively assembled into a subassembly element, as shown in Figure 3(a). This element comprises an elastic beam element, elastic joint element J₁ at node 1, and elastic joint element J₂ at node 2. Therefore, the subassembly element consists of two nodes, with each node having three translational degrees of freedom (DOFs), three rotational DOFs, totaling 12 DOFs. To streamline the derivation of the subassembly element static equation, the coordinate frames were established as follows: coordinate frame {J₁} at Joint 1, coordinate frame {J₂} at Joint 2, and beam element coordinate frame {s}. To reduce the calculation burden resulting from the redundant coordinate frame, the coordinate frame of the subassembly is considered consistent with that of the beam element.

Figure 3

Subassembly element: (a) unsupported subassembly element, (b) node 1 fixed, (c) node 2 fixed

The statics equation of the subassembly element can be expressed as follows.

$$\left[ {\begin{array}{*{20}c} {{}^{{\text{s}}}{\varvec{W}}_{1} } \\ {{}^{{\text{s}}}{\varvec{W}}_{2} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {{}^{{\text{s}}}{\varvec{K}}_{{{\text{s}}11}} } & {{}^{{\text{s}}}{\varvec{K}}_{{{\text{s}}12}} } \\ {{}^{{\text{s}}}{\varvec{K}}_{{{\text{s}}21}} } & {{}^{{\text{s}}}{\varvec{K}}_{{{\text{s}}22}} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {{}^{{\text{s}}}{\varvec{u}}_{1} } \\ {{}^{{\text{s}}}{\varvec{u}}_{2} } \\ \end{array} } \right] = {}^{{\text{s}}}{\varvec{K}}_{{\text{s}}} \left[ {\begin{array}{*{20}c} {{}^{{\text{s}}}{\varvec{u}}_{1} } \\ {{}^{{\text{s}}}{\varvec{u}}_{2} } \\ \end{array} } \right],$$

(1)

where ^sW₁ and ^sW₂ are the forces acting on nodes 1 and 2 of the subassembly element, respectively. ^su₁ and ^su₂ represent the displacement column vectors of nodes 1 and 2, respectively, caused by the applied forces. K_s denotes 12×12 subassembly element stiffness matrix, where K_sij represents the 6×6 block matrix of K_s. The top-left symbol s indicates that the vector or matrix (·) is represented in the coordinate frame {s}.

We now consider two special cases [19] to calculate the subassembly element stiffness matrix, where node 1 is fixed, as shown in Figure 3(b), and the constraint equation is ^su₁ = 0. In this case, Eq. (1) can be expressed as:

$$\left\{ \begin{gathered} {}^{{\text{s}}}{\varvec{W}}_{1}\, =\,{}^{{\text{s}}}{\varvec{K}}_{{{\text{s}}12}} {}^{{\text{s}}}{\varvec{u}}_{2} , \hfill \\ {}^{{\text{s}}}{\varvec{W}}_{2}\, =\,{}^{{\text{s}}}{\varvec{K}}_{{{\text{s}}22}} {}^{{\text{s}}}{\varvec{u}}_{2} . \hfill \\ \end{gathered} \right.$$

(2)

The mapping relationship of node forces can be obtained from the element equilibrium equation.

$${}^{{\text{s}}}{\varvec{W}}_{1}\,= \,- \left[ {\begin{array}{*{20}c} {{\varvec{I}}_{3} } & {{\varvec{0}}_{3} } \\ {[{\varvec{L}}_{12} \times ]} & {{\varvec{I}}_{3} } \\ \end{array} } \right]{}^{{\text{s}}}{\varvec{W}}_{2}\, = \,{\varvec{D}}_{12} {}^{{\text{s}}}{\varvec{W}}_{2} ,$$

(3)

where L₁₂ is the vector from node 1 to node 2, and [L₁₂×] is the skew-symmetric matrix derived from vector L₁₂.

The strain energy of the cantilever subassembly element owing to the action of the node force at node 2 is as follows:

$$\begin{gathered} U_{{W2}} = \frac{1}{2}{}^{{\text{s}}}{\varvec{W}}_{2}^{{\text{T}}} \,{}_{{\text{s}}}^{{{\text{J}}_{2} }} {\varvec{T}}^{{\text{T}}} \,{}^{{{\text{J}}_{2} }}{\varvec{C}}_{{J_{2} }} \,{}_{{\text{s}}}^{{{\text{J}}_{2} }} {\varvec{T}}{}^{{\text{s}}}{\varvec{W}}_{2} + \frac{1}{2}\,{}^{{\text{s}}}{\varvec{W}}_{2}^{{\text{T}}} \,{}^{{\text{s}}}{\varvec{C}}_{b} \,{}^{{\text{s}}}{\varvec{W}}_{2} \hfill \\ + \frac{1}{2}{}^{{\text{s}}}{\varvec{W}}_{2}^{{\text{T}}} \,{\varvec{D}}_{{12}}^{{\text{T}}} \,{}_{{\text{s}}}^{{{\text{J}}_{1} }} {\varvec{T}}^{{\text{T}}} \,{}^{{{\text{J}}_{1} }}{\varvec{C}}_{{J_{1} }} \,{}_{{\text{s}}}^{{{\text{J}}_{1} }} {\varvec{TD}}_{{12}}^{{}} {}^{{\text{s}}}{\varvec{W}}_{2} , \hfill \\ \end{gathered}$$

(4)

where U_W2 is the strain energy of the subassembly element generated by wrench W₂, ${}_{s}^{{{\text{J}}_{i} }} T = {\text{diag}}[{}_{s}^{{{\text{J}}_{i} }} R\quad {}_{s}^{{{\text{J}}_{i} }} R]$, ${}_{{\text{s}}}^{{{\text{J}}_{i} }} {\varvec{R}}$ is the rotation matrix from the subassembly element coordinate frame {s} to the joint coordinate frame {J_i}, and ${}^{{{\text{J}}_{i} }}{\varvec{C}}_{{{\text{J}}_{i} }}$ and ^sC_b are the compliance matrices of joint J_i and the cantilever beam element in the local coordinate frame, respectively.

Eq. (5) is obtained based on the strain energy and Castigliano’s second theorem.

$$\left\{ \begin{gathered} {}^{{\text{s}}}{\varvec{u}}_{2} = \frac{{\partial U_{{{\varvec{W}}_{2} }} }}{{\partial {}^{{\text{s}}}{\varvec{W}}_{2} }} = {}^{{\text{s}}}{\varvec{C}}_{{{\text{s}}22}} {}^{{\text{s}}}{\varvec{W}}_{2} , \hfill \\ {}^{{\text{s}}}{\varvec{C}}_{{{\text{s}}22}} = {}_{{\text{s}}}^{{{\text{J}}_{2} }} {\varvec{T}}^{{\text{T}}} \,{}^{{{\text{J}}_{2} }}{\varvec{C}}_{{{\text{J}}_{2} }} {}_{{\text{s}}}^{{{\text{J}}_{2} }} {\varvec{T}} + {}^{{\text{s}}}{\varvec{C}}_{b} + {\varvec{D}}_{{12}}^{{\text{T}}} \;{}_{{\text{s}}}^{{{\text{J}}_{1} }} {\varvec{T}}^{{\text{T}}} \;{}^{{{\text{J}}_{1} }}{\varvec{C}}_{{{\text{J}}_{1} }} \;{}_{{\text{s}}}^{{{\text{J}}_{1} }} {\varvec{TD}}_{{12}}^{{}} . \hfill \\ \end{gathered} \right.$$

(5)

Combining Eqs. (2) and (5), one can have

$${}^{{\text{s}}}{\varvec{K}}_{{{\text{s}}22}}\,=\,{}^{{\text{s}}}{\varvec{C}}_{{{\text{s}}22}}^{ - 1} .$$

(6)

Similarly, combining Eqs. (2) and (3), we obtain:

$${}^{{\text{s}}}{\varvec{K}}_{{{\text{s}}12}} \,= \,{\varvec{D}}_{12} {}^{{\text{s}}}{\varvec{K}}_{{{\text{s}}22}} .$$

(7)

Second, node 2 is fixed, as shown in Figure 3(c), and the corresponding boundary conditions are ^su₂ = 0. In this case, Eq. (1) can be expressed as:

$$\left\{ \begin{gathered} {}^{{\text{s}}}{\varvec{W}}_{1} \,=\,{}^{{\text{s}}}{\varvec{K}}_{{{\text{s}}11}} {}^{{\text{s}}}{\varvec{u}}_{1} , \hfill \\ {}^{{\text{s}}}{\varvec{W}}_{2}\, =\,{}^{{\text{s}}}{\varvec{K}}_{{{\text{s}}21}} {}^{{\text{s}}}{\varvec{u}}_{1} . \hfill \\ \end{gathered} \right.$$

(8)

The mapping relationship of node forces is given by.

$${}^{{\text{s}}}{\varvec{W}}_{2} \,= \,-\left[ {\begin{array}{*{20}c} {{\varvec{I}}_{3} } & {{\varvec{0}}_{3} } \\ { - [{\varvec{L}}_{12} \times ]} & {{\varvec{I}}_{3} } \\ \end{array} } \right]{}^{{\text{s}}}{\varvec{W}}_{1} \,= \,{\varvec{D}}_{21} {}^{{\text{s}}}{\varvec{W}}_{1} .$$

(9)

Similarly, the mapping relationship between the displacement column vector and wrench of node 1 can be obtained as follows:

$${}^{{\text{s}}}{\varvec{u}}_{1} = ({}_{{\text{s}}}^{{{\text{J}}_{1} }} {\varvec{T}}^{{\text{T}}} \;{}^{{{\text{J}}_{1} }}{\varvec{C}}_{{{\text{J}}_{1} }} \;{}_{{\text{s}}}^{{{\text{J}}_{1} }} {\varvec{T}} + {}^{{\text{s}}}{\varvec{C}}_{b} + {\varvec{D}}_{{21}}^{{\text{T}}} \;{}_{{\text{s}}}^{{{\text{J}}_{2} }} {\varvec{T}}^{{\text{T}}} \;{}^{{{\text{J}}_{2} }}{\varvec{C}}_{{{\text{J}}_{2} }} \;{}_{{\text{s}}}^{{{\text{J}}_{2} }} {\varvec{TD}}_{{21}}^{{}} ){}^{{\text{s}}}{\varvec{W}}_{1} .$$

(10)

Considering the standard direction of the coordinate axes, the expression for block matrix ^sK_s11 can be obtained as

(11)

Combining Eqs. (8) and (9), one can have

$${}^{\text{s}}{\varvec{K}}_{s21}\, =\,{\varvec{D}}_{21} {}^{\text{s}}{\varvec{K}}_{s11} .$$

(12)

Eqs. (5) and (11) show that when considering the joint to be rigid, the stiffness matrix of the subassembly element simplifies to that of the beam element, preventing numerical calculations from becoming unstable when the stiffness corresponding to the free motion direction of the joints is equal to zero.

Notably, the subassembly element stiffness matrix is not a constant matrix, even in the element coordinate system, but a posture-dependent matrix determined by the rotation matrix from the joint coordinate frame to the element coordinate system. The advantage of establishing the subassembly element stiffness matrix is that it enables the direct use multipoint constraint theory [24] to establish the joint constraint relationship and extract the IDCs of the constraint nodes. This facilitates the rapid establishment of the overall stiffness matrix of the structure, bypassing the need for complex deformation coordination equations. Consequently, this approach significantly facilitates the evaluation of the stiffness and strength performance of the structure.

2.2 IDCs of Constraint Points

2.2.1 Body-To-Body

2.2.1.1 Universal Joint

Figure 4 shows examples of joints commonly encountered in PMs. The U-joint shown in Figure 4(a) possesses two DOFs, allowing two independent rotations between the two overlapping nodes connected by this joint. Thus, the two nodes have eight IDCs, comprising six displacement coordinates of point j (i) and two angular displacement coordinates of point i (j). Next, we extract two independent angular displacement coordinates of point i as an example.

Figure 4

Examples of joints: (a) U-joint, (b) R-joint, (c) S-joint, (d) P-joint, (e) C-joint, (f) screw joint

The compatibility condition between nodes i and j can be obtained as follows.

$$\left\{ \begin{gathered} {{\varvec{\Delta}}}_{i} = {{\varvec{\Delta}}}_{j} ,\quad \hfill \\ {}^{J}\varphi_{iz} = \left[ {\begin{array}{*{20}c} 0 & 0 & 1 \\ \end{array} } \right]{\varvec{R}}_{U}^{ - 1} {\varvec{\varphi }}_{j} \,= \,{\varvec{Q}}_{U} {\varvec{\varphi }}_{j} , \hfill \\ \end{gathered} \right.$$

(13)

where, Q_U = [0 0 1]R_U ^-1, ^Jφ_iz is z-axis component of angular displacement coordinate of point i in the joint coordinate frame. Δ_i and Δ_j are the linear displacement coordinates of points i and j, respectively, in the global coordinate frame. φ_j is the angular displacement coordinate of the point j in the global coordinate frame. For simplicity, the global coordinate system identifier in the upper-left corner of the vector is omitted in this study. R_U is the rotation matrix from the U-joint coordinate frame to the global coordinate frame.

Eq. (14) can be obtained according to rotation matrix

$${\varvec{\varphi }}_{i} = {\varvec{R}}_{U} {}^{J}{\varvec{\varphi }}_{i} .$$

(14)

Expanding Eq. (14), one can have

$$\left\{ \begin{gathered} \varphi_{ix} = R_{U} (1,1){}^{J}\varphi_{ix} + R_{U} (1,2){}^{J}\varphi_{iy} + R_{U} (1,3){}^{J}\varphi_{iz} , \hfill \\ \varphi_{iy} = R_{U} (2,1){}^{J}\varphi_{ix} + R_{U} (2,2){}^{J}\varphi_{iy} + R_{U} (2,3){}^{J}\varphi_{iz} , \hfill \\ \varphi_{iz} = R_{U} (3,1){}^{J}\varphi_{ix} + R_{U} (3,2){}^{J}\varphi_{iy} + R_{U} (3,3){}^{J}\varphi_{iz} , \hfill \\ \end{gathered} \right.$$

(15)

where R_U(j, k) is the element of the j^th row and k^th column of the matrix R_U.

The constraint equations in Eq. (15) and the second formula in Eq. (13) contain only two independent algebraic equations. Specifically, φ_ix and φ_iy, φ_iy and φ_iz, or φ_ix and φ_iz can be considered as the two independent angular displacement coordinates of point i. In reality, some configurations remain in the workspace where the basic plane of the global coordinate system is parallel to the plane composed of the U-joint axes. In such cases, only the angular displacement coordinates along the axes components of the basic plane of the global coordinate system can be used as IDCs to avoid singularities that occur at these special configurations. For instance, if the x-y (y-z / x-z) plane of global coordinate frame is parallel to the plane of U-joint axes, only the set of φ_ix and φ_iy (φ_iy and φ_iz / φ_ix and φ_iz) can be extracted as independent angular displacement coordinates. The proof and mapping relationship between the independent and dependent displacement coordinates are as follows.

Substituting Eq. (13) into Eq. (15) and solving the first two formulas of Eq. (15), we obtain

$$\left\{ \begin{gathered} {}^{J}\varphi _{{ix}} = \frac{{ - \left( {R_{U} (2,2)R_{U} (1,3) - R_{U} (1,2)R_{U} (2,3)} \right){\varvec{Q}}_{U} {\varvec{\varphi }}_{j} }}{{R_{U} (1,1)R_{U} (2,2) - R_{U} (1,2)R_{U} (2,1)}} \hfill \\ \quad \quad + \frac{{R_{U} (2,2)\varphi _{{ix}} - R_{U} (1,2)\varphi _{{iy}} }}{{R_{U} (1,1)R_{U} (2,2) - R_{U} (1,2)R_{U} (2,1)}}, \hfill \\ {}^{J}\varphi _{{iy}} = \frac{{R_{U} (2,1)\varphi _{{ix}} - R_{U} (1,1)\varphi _{{iy}} }}{{R_{U} (1,2)R_{U} (2,1) - R_{U} (1,1)R_{U} (2,2)}} \hfill \\ \quad - \frac{{\left( {R_{U} (2,1)R_{U} (1,3) - R_{U} (1,1)R_{U} (2,3)} \right){\varvec{Q}}_{U} {\varvec{\varphi }}_{j} }}{{R_{U} (1,2)R_{U} (2,1) - R_{U} (1,1)R_{U} (2,2)}}. \hfill \\ \end{gathered} \right.$$

(16)

Substituting Eq. (16) into the third Formula of Eq. (15), we obtain

$$\varphi_{iz} \,= \,a_{{{\text{U}}ix}} \varphi_{ix} + a_{Uiy} \varphi_{iy} + a_{Uip} {\varvec{Q}}_{U} {\varvec{\varphi }}_{j} = {\varvec{N}}_{U} \left[ {\begin{array}{*{20}c} {\varphi_{ix} } \\ {\varphi_{iy} } \\ {{\varvec{\varphi }}_{j} } \\ \end{array} } \right],$$

(17)

where $a_{{Uip}} = \frac{{R_{U} (3,2)\left( {R_{U} (1,3)R_{U} (2,1) - R_{U} (1,1)R_{U} (2,3)} \right)}}{{R_{U} (1,1)R_{U} (2,2) - R_{U} (1,2)R_{U} (2,1)}}$$- \frac{{R_{U} (3,1)(R_{U} (1,3)R_{U} (2,2) - R_{U} (1,2)R_{U} (2,3))}}{{R_{U} (1,1)R_{U} (2,2) - R_{U} (1,2)R_{U} (2,1)}} + R_{U} (3,3)$,$a_{Uix} = \frac{{R_{U} (3,1)R_{U} (2,2) - R_{U} (3,2)R_{U} (2,1)}}{{R_{U} (1,1)R_{U} (2,2) - R_{U} (1,2)R_{U} (2,1)}}$,$a_{Uiy} = \frac{{R_{U} (1,1)R_{U} (3,2) - R_{U} (1,2)R_{U} (3,1)}}{{R_{U} (1,1)R_{U} (2,2) - R_{U} (1,2)R_{U} (2,1)}}$,${\varvec{N}}_{U} = \left[ {\begin{array}{*{20}c} {a_{Uix} } & {a_{Uiy} } & {a_{Uip} {\varvec{Q}}_{U} } \\ \end{array} } \right]$.

If φ_ix and φ_iz, or φ_iy and φ_iz are considered as independent angular displacement coordinates, the following equations can be obtained.

$$\varphi_{iy}\,=\,a^{\prime}_{Uix} \varphi_{ix} + a^{\prime}_{Uiz} \varphi_{iz} + a^{\prime}_{Uip} {\varvec{Q}}_{U} {\varvec{\varphi }}_{j} = {\varvec{N^{\prime}}}_{U} \left[ {\begin{array}{*{20}c} {\varphi_{ix} } \\ {\varphi_{iz} } \\ {{\varvec{\varphi }}_{j} } \\ \end{array} } \right],$$

(18)

where, $a^{\prime}_{Uix} = \frac{{R_{U} (2,1)R_{U} (3,2) - R_{U} (2,2)R_{U} (3,1)}}{{R_{U} (1,1)R_{U} (3,2) - R_{U} (1,2)R_{U} (3,1)}}$,$a^{\prime}_{Uiz} = \frac{{R_{U} (1,1)R_{U} (2,2) - R_{U} (1,2)R_{U} (2,1)}}{{R_{U} (1,1)R_{U} (3,2) - R_{U} (1,2)R_{U} (3,1)}}$,$a_{{Uip}}^{\prime } = R_{U} (2,3) + \frac{{R_{U} (2,2)\left( {R_{U} (1,3)R_{U} (3,1) - R_{U} (1,1)R_{U} (1,3)} \right)}}{{R_{U} (1,1)R_{U} (3,2) - R_{U} (1,2)R_{U} (3,1)}} - \frac{{R_{U} (2,1)\left( {R_{U} (1,3)R_{U} (3,2) - R_{U} (1,2)R_{U} (3,3)} \right)}}{{R_{U} (1,1)R_{U} (3,2) - R_{U} (1,2)R_{U} (3,1)}}$.

And

$$\varphi_{ix} \, = \,a^{\prime\prime}_{Uiy} \varphi_{iy} + a^{\prime\prime}_{Uiz} \varphi_{iz} + a^{\prime\prime}_{Uip} {\varvec{Q}}_{U} {\varvec{\varphi }}_{j} = {\varvec{N^{\prime\prime}}}_{U} \left[ {\begin{array}{*{20}c} {\varphi_{iy} } \\ {\varphi_{iz} } \\ {{\varvec{\varphi }}_{j} } \\ \end{array} } \right],$$

(19)

where $a^{\prime\prime}_{Uiy} = \frac{{R_{U} (1,1)R_{U} (3,2) - R_{U} (1,2)R_{U} (3,1)}}{{R_{U} (2,1)R_{U} (3,2) - R_{U} (2,2)R_{U} (3,1)}}$,$a^{\prime\prime}_{Uiz} = \frac{{R_{U} (1,2)R_{U} (2,1) - R_{U} (1,1)R_{U} (2,2)}}{{R_{U} (1,2)R_{U} (3,2) - R_{U} (2,2)R_{U} (3,1)}}$,$a_{{Uip}}^{{\prime \prime }} = R_{U} (1,3) + \frac{{R_{U} (1,2)\left( {R_{U} (2,3)R_{U} (3,1) - R_{U} (2,1)R_{U} (3,3)} \right)}}{{R_{U} (2,1)R_{U} (3,2) - R_{U} (2,2)R_{U} (3,1)}} - \frac{{R_{U} (1,1)\left( {R_{U} (2,3)R_{U} (3,2) - R_{U} (2,2)R_{U} (3,3)} \right)}}{{R_{U} (2,1)R_{U} (3,2) - R_{U} (2,2)R_{U} (3,1)}}$.

Considering that the x-y plane is parallel to the plane of the U-joint axes in some configurations, the rotation matrix can be expressed as follows:

$${\varvec{R}}_{U} = \left[ {\begin{array}{*{20}c} { \pm 1} & 0 & 0 \\ 0 & { \pm 1} & 0 \\ 0 & 0 & { \pm 1} \\ \end{array} } \right].$$

(20)

Apparently, the denominators of $a^{\prime}_{Uix}$, $a^{\prime}_{Uiz}$, $a^{\prime}_{Uip}$, $a^{\prime\prime}_{Uiy}$, $a^{\prime\prime}_{Uiz}$, and $a^{\prime\prime}_{Uip}$ are equal to zero, making the matrices ${\varvec{N^{\prime}}}_{U}$ and ${\varvec{N^{\prime\prime}}}_{U}$ singular in these configurations. Hence, only φ_Aix and φ_Aiy can be extracted as the two independent angular displacement coordinates of point i in the global coordinate frame.

Accordingly, the IDCs of the two nodes connected by the U-joint can be expressed as

$${\varvec{u}}_{U,id} = \left[ {\varphi_{ix} \;\varphi_{iy} \;{\varvec{u}}_{j} } \right].$$

(21)

where ${\varvec{u}}_{U,id}$ is the IDCs of the two overlapping nodes connected by a U-joint.

2.2.1.2 Revolute Joint

The R-joint shown in Figure 4(b) possesses one DOF, enabling independent rotation between the two nodes it connects. Thus, these two nodes exhibit seven IDCs. The compatibility condition between nodes i and j can be obtained as follows:

$${{\varvec{\Delta}}}_{i} = {{\varvec{\Delta}}}_{j} ,\quad \left[ \begin{gathered} {}^{J}\varphi_{ix} \hfill \\ {}^{J}\varphi_{iz} \hfill \\ \end{gathered} \right] = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & 0 & 1 \\ \end{array} } \right]{\varvec{R}}_{R}^{ - 1} {\varvec{\varphi }}_{j} \, = \,{\varvec{Q}}_{R} {\varvec{\varphi }}_{j} ,$$

(22)

where ${\varvec{Q}}_{R}\, = \,\left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & 0 & 1 \\ \end{array} } \right]{\varvec{R}}_{R}^{ - 1}$.

Consider that the y-axis of the global coordinate frame is parallel to the R-joint axis in some configurations. In such cases, only φ_iy can be chosen as an independent angular displacement coordinate for point i. Following the calculation procedure outlined above for the U-joint, we can derive the following equation.

$$\left[ {\begin{array}{*{20}c} {\varphi_{ix} } \\ {\varphi_{iz} } \\ \end{array} } \right]{ = }\left[ {\begin{array}{*{20}c} {\frac{{R_{R} (1,2)}}{{R_{R} (2,2)}}} & {{\varvec{a}}_{Rix} - \frac{{R_{R} (1,2){\varvec{a}}_{Riy} }}{{R_{R} (2,2)}}} \\ {\frac{{R_{R} (3,2)}}{{R_{R} (2,2)}}} & {{\varvec{a}}_{Riz} - \frac{{R_{R} (3,2){\varvec{a}}_{Riy} }}{{R_{R} (2,2)}}} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\varphi_{iy} } \\ {{\varvec{\varphi }}_{j} } \\ \end{array} } \right] = {\varvec{N}}_{R} \left[ {\begin{array}{*{20}c} {\varphi_{iy} } \\ {{\varvec{\varphi }}_{j} } \\ \end{array} } \right],$$

(23)

where ${\varvec{a}}_{Rix} = R_{R} (1,1){\varvec{Q}}_{R} (1,:) + R_{R} (1,3){\varvec{Q}}_{R} (2,:)$,${\varvec{a}}_{Riy} = R_{R} (2,1){\varvec{Q}}_{R} (1,:)$$+ R_{R} (2,3){\varvec{Q}}_{R} (2,:)$,${\varvec{a}}_{Riz} = R_{R} (3,1){\varvec{Q}}_{R} (1,:) + R_{R} (3,3){\varvec{Q}}_{R} (2,:)$, Q_R(j,:) are the jth row of the matrix Q_R.

Accordingly, the IDCs of the two overlapping nodes connected by an R-joint can be expressed as

$${\varvec{u}}_{R,id} = \left[ {\varphi_{iy} \;{\varvec{u}}_{j} } \right],$$

(24)

where ${\varvec{u}}_{R,id}$ is the IDCs of the two nodes connected by the R-joint.

2.2.1.3 Spherical Joint

The S-joint, shown in Figure 4(c), features three DOFs, allowing three independent rotations between the two nodes it connects. Thus, the two nodes have nine IDCs. The compatibility condition and IDCs of the two nodes are obtained as follows:

$${{\varvec{\Delta}}}_{i} = {{\varvec{\Delta}}}_{j} ,$$

(25)

$${\varvec{u}}_{S,id} = \left[ {\varphi_{ix} \;\varphi_{iy} \;\varphi_{iz} \;{\varvec{u}}_{j} } \right].$$

(26)

2.2.1.4 Prismatic Joint

Similarly, as shown in Figure 4(d), considering that the y-axis of the global coordinate frame is parallel to the P-joint axis in some configurations, the IDCs of the P-joint and the mapping relationship between the independent and dependent coordinates are given by

$${\varvec{u}}_{P,id} = \left[ {\Delta_{iy} \;{\varvec{u}}_{j} } \right],$$

(27)

$$\left\{ \begin{gathered} {\varvec{\varphi }}_{i}\,=\,{\varvec{\varphi }}_{j} ,\quad \hfill \\ \left[ {\begin{array}{*{20}c} {\Delta_{ix} } \\ {\Delta_{iz} } \\ \end{array} } \right]{ = }{\varvec{N}}_{P} \left[ {\begin{array}{*{20}c} {\Delta_{iy} } \\ {{{\varvec{\Delta}}}_{j} } \\ \end{array} } \right], \hfill \\ \end{gathered} \right.$$

(28)

where N_P can be obtained by replacing the rotation matrix R_R in N_R with R_P.

2.2.1.5 Cylindrical Joint

A cylindrical joint can be considered as a combination of P- and R-joints. In such a scenario, the independent displacement coordinates and their mapping relationship with the dependent displacement coordinates are given as follows:

$${\varvec{u}}_{C,id} = \left[ {\Delta_{iy} \;\varphi_{iy} \;{\varvec{u}}_{j} } \right],$$

(29)

$$\left[ {\begin{array}{*{20}c} {\Delta_{ix} } \\ \begin{gathered} \Delta_{iz} \hfill \\ \varphi_{ix} \hfill \\ \varphi_{iz} \hfill \\ \end{gathered} \\ \end{array} } \right]{ = }\left[ {\begin{array}{*{20}c} {{\varvec{N}}_{P} } & {{\varvec{0}}_{2 \times 4} } \\ {{\varvec{0}}_{2 \times 4} } & {{\varvec{N}}_{R} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\varphi_{iy} } \\ {{\varvec{\varphi }}_{j} } \\ \end{array} } \right] = {\varvec{N}}_{C} \left[ {\begin{array}{*{20}c} {\Delta_{iy} } \\ \begin{gathered} {{\varvec{\Delta}}}_{j} \hfill \\ \varphi_{iy} \hfill \\ {\varvec{\varphi }}_{j} \hfill \\ \end{gathered} \\ \end{array} } \right].$$

(30)

2.2.1.6 Screw Joint

Figure 4(f) shows the two-node screw joint element, similar to a cylindrical element in construction. However, while the cylindrical joint element has two free relative DOFs, the screw joint has only one DOF. In a screw joint, the pitch p correlates the relative rotation angle to the relative translational displacement along the axis of the screw. Similarly, the independent displacement coordinates of the screw joint element were considered to be

$${\varvec{u}}_{W,id} = \left[ {\varphi_{iy} \;{\varvec{u}}_{j} } \right].$$

(31)

The constraint equations can be expressed as follows.

$$\left\{ \begin{gathered} \left[ \begin{gathered} {}^{J}\Delta _{{ix}} \hfill \\ {}^{J}\Delta _{{iz}} \hfill \\ \end{gathered} \right] = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & 0 & 1 \\ \end{array} } \right]{\varvec{R}}_{W} ^{{ - 1}} {\varvec{\Delta }}_{j} = {\varvec{Q}}_{{W1}} {\varvec{\Delta }}_{j} , \hfill \\ {}^{J}\Delta _{{iy}} = {}^{J}\Delta _{{jy}} - p\left( {{}^{J}\varphi _{{jy}} - {}^{J}\varphi _{{iy}} } \right) = \left[ {\begin{array}{*{20}c} 0 & 1 & 0 \\ \end{array} } \right]{\varvec{R}}_{W} ^{{ - 1}} \hfill \\ \quad \quad \left[ {{\varvec{\Delta }}_{j} - p\left( {{\varvec{\varphi }}_{j} - {\varvec{\varphi }}_{i} } \right)} \right] = {\varvec{Q}}_{{W2}} \left[ {{\varvec{\Delta }}_{j} - p\left( {{\varvec{\varphi }}_{j} - {\varvec{\varphi }}_{i} } \right)} \right], \hfill \\ \left[ \begin{gathered} {}^{J}\varphi _{{ix}} \hfill \\ {}^{J}\varphi _{{iz}} \hfill \\ \end{gathered} \right] = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & 0 & 1 \\ \end{array} } \right]{\varvec{R}}_{W} ^{{ - 1}} {\varvec{\varphi }}_{j} . \hfill \\ \end{gathered} \right.$$

(32)

Refer to Eq. (23) to extract the independent angular displacement coordinates of the revolute joint in the global coordinate frame. The third formula in Eq. (32) can be expressed as:

$$\begin{gathered} \left[ {\begin{array}{*{20}c} \begin{gathered} \varphi_{ix} \hfill \\ \varphi_{iy} \hfill \\ \end{gathered} \\ {\varphi_{iz} } \\ \end{array} } \right]{ = }\left[ {\begin{array}{*{20}c} {\frac{{R_{W} (1,2)}}{{R_{W} (2,2)}}} & {{\varvec{a}}_{Wix} - \frac{{R_{W} (1,2){\varvec{a}}_{Wiy} }}{{R_{W} (2,2)}}} \\ 1 & {{\varvec{0}}_{1 \times 3} } \\ {\frac{{R_{W} (3,2)}}{{R_{W} (2,2)}}} & {{\varvec{a}}_{Wiz} - \frac{{R_{W} (3,2){\varvec{a}}_{iy} }}{{R_{W} (2,2)}}} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\varphi_{iy} } \\ {{\varvec{\varphi }}_{j} } \\ \end{array} } \right] \hfill \\ \quad \quad = {\varvec{N}}_{W\varphi i} \varphi_{iy} + {\varvec{N}}_{W\varphi j} {\varvec{\varphi }}_{j} , \hfill \\ \end{gathered}$$

(33)

where a_Wix, a_Wiy, and a_Wiz can be obtained by replacing the R_R in a_Rix, a_Riy, and a_Riz with R_W, respectively, ${\varvec{N}}_{W\varphi i} = \left[ {\begin{array}{*{20}c} {\frac{{R_{W} (1,2)}}{{R_{W} (2,2)}}} & 1 & {\frac{{R_{W} (3,2)}}{{R_{W} (2,2)}}} \\ \end{array} } \right]^{{\text{T}}}$ and ${\varvec{N}}_{W\varphi j} = \left[ {\begin{array}{*{20}c} {{\varvec{a}}_{ix} - \frac{{R_{W} (1,2){\varvec{a}}_{iy} }}{{R_{W} (2,2)}}} & {{\varvec{0}}_{1 \times 3} } & {{\varvec{a}}_{iz} - \frac{{R_{W} (3,2){\varvec{a}}_{iy} }}{{R_{W} (2,2)}}} \\ \end{array} } \right]^{{\text{T}}}$.

Substituting Eq. (33) into the second formula of Eq. (32), we obtain

$${}^{J}\Delta_{iy} = p{\varvec{Q}}_{W2} {\varvec{N}}_{W\varphi i} \varphi_{iy} + {\varvec{Q}}_{W2} {{\varvec{\Delta}}}_{j} - p{\varvec{Q}}_{W2} ({\varvec{E}}_{3} - {\varvec{N}}_{W\varphi j} ).$$

(34)

According to the coordinate frame transformation, one can have

$${{\varvec{\Delta}}}_{i} = {\varvec{R}}_{W} {}^{J}{{\varvec{\Delta}}}_{i} .$$

(35)

Substituting Eq. (34) and the first formula of Eq. (32) into Eq. (35), we obtain

$$\left[ \begin{gathered} \Delta_{ix} \hfill \\ \Delta_{iy} \hfill \\ \Delta_{iz} \hfill \\ \end{gathered} \right] = {\varvec{N}}_{\Delta i} \left[ \begin{gathered} \varphi_{iy} \hfill \\ {{\varvec{\Delta}}}_{j} \hfill \\ {\varvec{\varphi }}_{j} \hfill \\ \end{gathered} \right],$$

(36)

where ${\varvec{N}}_{\Delta i} = \left[ {\begin{array}{*{20}c} {pR_{W} (1,2){\varvec{Q}}_{W2} {\varvec{N}}_{\varphi i} } & {R_{W} (1,1){\varvec{Q}}_{W1} (1,:) + R_{W} (1,2){\varvec{Q}}_{W2} + R_{W} (1,3){\varvec{Q}}_{W1} (2,:)} \\ {pR_{W} (2,2){\varvec{Q}}_{W2} {\varvec{N}}_{\varphi i} } & {R_{W} (2,1){\varvec{Q}}_{W1} (1,:) + R_{W} (2,2){\varvec{Q}}_{W2} + R_{W} (2,3){\varvec{Q}}_{W1} (2,:)} \\ {pR_{W} (3,2){\varvec{Q}}_{W2} {\varvec{N}}_{\varphi i} } & {R_{W} (3,1){\varvec{Q}}_{W1} (1,:) + R_{W} (3,2){\varvec{Q}}_{W2} + R_{W} (3,3){\varvec{Q}}_{W1} (2,:)} \\ \end{array} } \right.$$\left. {\begin{array}{*{20}c} {pR_{W} (1,2){\varvec{Q}}_{W2} ({\varvec{N}}_{\varphi j} - E_{3} )} \\ {pR_{W} (2,2){\varvec{Q}}_{W2} ({\varvec{N}}_{\varphi j} - E_{3} )} \\ {pR_{W} (3,2){\varvec{Q}}_{W2} ({\varvec{N}}_{\varphi j} - E_{3} )} \\ \end{array} } \right]$.

Eqs. (33) and (36) define the mapping matrix between the dependent and independent displacement coordinates of the screw joints.

2.2.2 Body-To-Ground

Body-to-ground can be considered a special case of body-to-body. In this case, node j is fixed; therefore, its displacement coordinate, equals zero. Thus, the IDCs and the mapping relationship between the independent and dependent displacement coordinates can be obtained by setting u_j = 0.

2.2.3 Rigid Body Motion

Kinematic relationships were used to model the small displacements of the rigid element. The constraint modeling of the rigid body motion defined by nodes i and j is given as follows:

$${\varvec{u}}_{i} = \left[ {\begin{array}{*{20}c} {{\varvec{E}}_{3} } & {[{\varvec{L}}_{ij} \times ]} \\ {{\varvec{0}}_{3} } & {{\varvec{E}}_{3} } \\ \end{array} } \right]{\varvec{u}}_{j} ,$$

(37)

where E₃ and 0₃ represent the 3×3 identity and zero matrices, respectively, [L_ij×] is the skew-symmetric matrix defined by the vector L_ij, which links nodes i to j.

Thus, a rigid body has only six IDCs.

The IDCs and corresponding constraint equations of the nodes connected by various joints commonly encountered in engineering are presented in Appendix. The analytical static equation of the structure can be rapidly assembled by referring to Appendix. Thus, the model is computationally efficient because simultaneous constraint equations and Lagrangian multipliers can be avoided.

2.3 Elastostatic Stiffness Model

Element stiffness modeling in the global coordinate frame can be obtained according to the rotation matrix.

$$\left[ {\begin{array}{*{20}c} {{\varvec{W}}_{1} } \\ {{\varvec{W}}_{2} } \\ \end{array} } \right] = {}_{\text{s}}{\varvec{T}}{}^{\text{s}}{\varvec{K}}_{\text{s}} {}_{\text{s}}{\varvec{T}}^{{\text{T}}} \left[ {\begin{array}{*{20}c} {{\varvec{u}}_{1} } \\ {{\varvec{u}}_{2} } \\ \end{array} } \right] = {\varvec{K}}_{\text{s}} \left[ {\begin{array}{*{20}c} {{\varvec{u}}_{1} } \\ {{\varvec{u}}_{2} } \\ \end{array} } \right],$$

(38)

where _sT = diag(_sR, _sR) and _sR is the rotation matrix from the element coordinate frame to the global coordinate frame. ${\varvec{K}}_{\text{s}} = {}_{\text{s}}{\varvec{T}}{}^{\text{s}}{\varvec{K}}_{\text{s}} {}_{\text{s}}{\varvec{T}}^{{\text{T}}}$.

The global IDCs of the PMs can be defined as follows.

$${\varvec{U}} = \left[ {{\varvec{u}}_{id}^{{\text{T}}} \;\;{\varvec{u}}_{o}^{{\text{T}}} } \right]^{{\text{T}}} ,$$

(39)

where u_o is the output node of the structure and u_id is the IDCs of other nodes, except the output node.

According to the analysis in Section 2.3, the mapping equations from the displacement coordinates of the subassembly elements of the open loops to the global IDCs of the closed-loop PMs are obtained as follows:

$${\varvec{u}}_{s,ij} = {\varvec{H}}_{ij} {\varvec{U}}\quad (i = 1,\;2,\; \ldots ,\;n;\;j = 1,\;2,\; \ldots ,\;m_{i} ),$$

(40)

where u_s,ij is the displacement column vector of the jth subassembly element of the ith chain. H_ij is the mapping matrix from the global IDCs of the structure to the displacement column vector of the jth subassembly element of the ith chain.

The total potential energy of the structure can be obtained by substituting Eq. (40) into Eq. (38).

$$E_{p} = \sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{{m_{i} }} {E_{ps,ij} } } = \frac{1}{2}\sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{{m_{i} }} {{\varvec{u}}_{s,ij}^{{\text{T}}} {\varvec{K}}_{s,ij}^{{}} {\varvec{u}}_{s,ij}^{{}} } } = \frac{1}{2}{\varvec{U}}_{{}}^{{\text{T}}} {\varvec{KU}},$$

(41)

with

$$\left\{ \begin{gathered} {\varvec{K}}\,=\,\sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{{m_{i} }} {{\varvec{K}}_{s,ij}^{g} } ,\;} \hfill \\ {\varvec{K}}_{s,ij}^{g} { = }{\varvec{H}}_{ij}^{{\text{T}}} {\varvec{K}}_{s,ij} {\varvec{H}}_{ij} , \hfill \\ \end{gathered} \right.$$

(42)

where M and K denote the overall mass and stiffness matrices of the mechanism, respectively. Kg s,ij is the contribution matrix of the j^th subassembly of the i^th chain to the overall stiffness matrix.

Accordingly, the stiffness modeling of the structure can be obtained using Eq. (41).

$${\varvec{KU}} = {\varvec{W}},$$

(43)

where W is the general force corresponding to the global IDCs U.

To establish the stiffness modeling of the output node, the global stiffness matrix of the mechanism can be written in the following block matrix form:

$${\varvec{K}} = \left[ {\begin{array}{*{20}c} {{\varvec{K}}_{ss} } & {{\varvec{K}}_{sm} } \\ {{\varvec{K}}_{ms} } & {{\varvec{K}}_{mm} } \\ \end{array} } \right],$$

(44)

where K_ss is a (k-6)×(k-6) matrix, K_sm is (k-6)×6 matrix, K_ms is 6×(k-6) matrix, and K_mm is 6×6 matrix, k is the dimension of the matrix K.

Therefore, the stiffness modeling of the output node can be obtained as follows.

$${\varvec{K}}_{o} {\varvec{u}}_{o} = {\varvec{W}}_{o} ,$$

(45)

where ${\varvec{K}}_{o} = {\varvec{T}}_{o}^{{\text{T}}} {\varvec{KT}}_{o}^{{}}$ is the stiffness matrix of the structure output node obtained using ${\varvec{T}}_{o}^{{}} = \left[ {\begin{array}{*{20}c} {{\overline{\varvec{T}}}_{o}^{{\text{T}}} } & {{\varvec{E}}_{6}^{{\text{T}}} } \\ \end{array} } \right]^{{\text{T}}}$ and ${\overline{\varvec{T}}}_{o}^{{}} = {\varvec{K}}_{ss}^{ - 1} {\varvec{K}}_{sm}$.

The values for the other IDCs can be obtained by substituting u_o into Eq. (45) into Eq. (43), and the dependent displacement values were obtained using Eq. (40). The node forces in the global and element coordinate systems are obtained using Eqs. (38) and (1). Once the element displacement column vector is in hand, the element strain column vector can be obtained through classical strain displacement conversion matrix.

$${}^{\text{s}}{{\varvec{\upvarepsilon}}}_{s} = {\varvec{B}}{}^{\text{s}}{\varvec{u}}_{s} .$$

(46)

Then, the element stress column vector can be obtained through the constitutive equations.

$${}^{s}{{\varvec{\upsigma}}}_{s} = {\varvec{D}}{}^{s}{{\varvec{\upvarepsilon}}}_{s} ,$$

(47)

where D is the elastic constant matrix.

So far, the static structural analysis has been completed.

3 Case Study 1: A Simple Single-Freedom Structure

In this section, we present a single-DOF structure to demonstrate the superiority of the proposed stiffness matrix for subassembly elements. Figure 5 shows a single-freedom structure, where rigid beam BC is connected to elastic beam AB with an elastic joint at point B, and elastic beam CD with an elastic joint at point D. The midpoint of rigid beam BC is denoted as the connection point between elastic beams AB and CD, while points A and D are fixed to the base. The compliance (stiffness) coefficients of the elastic beams AB and CD along the x-axis are c₁ (k₁) and c₂ (k₂), respectively. The compliance (stiffness) coefficients of elastic joints B and C along the x-axis are c_J1 (k_J1) and c_J2 (k_J2), respectively.

Figure 5

A single DOF structure

The traditional method treats the elastic joint as a spring element, and the reaction force at elastic joint B can be expressed as

$$f_{B} = k_{{{\text{J}}1}} (\Delta_{ox} - \Delta_{Bx} ),$$

(48)

where f_B is the reaction force at the point B, Δ_ox and Δ_Bx are the linear displacement of the points o and B along the x-axis, respectively.

According to the axial tensile and compressive deformation of material mechanics, one can have

$$\Delta_{Bx} = \frac{{f_{B} }}{{k_{1} }}.$$

(49)

Substituting Eq. (49) into Eq. (48), one can have

$$f_{B} = \frac{{k_{1} k_{{{\text{J}}1}} }}{{k_{1} + k_{{{\text{J}}1}} }}\Delta_{ox} .$$

(50)

Similarly, we can obtain the reaction force at the elastic joint C.

$$f_{C} = \frac{{k_{2} k_{{{\text{J2}}}} }}{{k_{2} + k_{{{\text{J2}}}} }}\Delta_{ox} .$$

(51)

Accordingly, the equilibrium equation of the rigid beam BC is given by

$$f = f_{C} + f_{B} .$$

(52)

Substituting Eqs. (50) and (51) into Eq. (52), we obtain

$$f = \left( {\frac{{k_{1} k_{{{\text{J}}1}} }}{{k_{1} + k_{{{\text{J}}1}} }} + \frac{{k_{2} k_{{{\text{J2}}}} }}{{k_{2} + k_{{{\text{J2}}}} }}} \right)\Delta _{{ox}} .$$

(53)

From Eq. (48) we can see that if the elastic joint is considered to be rigid, Δ_ox = Δ_Bx, making Eq. (48) singular, thereby resulting in numerical instability.

Subsequently, the proposed subassembly element was adopted to analyze the stiffness model, demonstrating its superiority.

Considering elastic beam AB and elastic joint B as subassembly element 1, and elastic beam CD and elastic joint C as subassembly element 2, the compliance coefficient along the x-axis of the cantilever subassembly element can be obtained using Eq. (54) as follows:

$$\left\{ \begin{gathered} c_{s1} = c_{1} + c_{{{\text{J1}}}} , \hfill \\ c_{s2} = c_{2} + c_{{{\text{J2}}}} , \hfill \\ \end{gathered} \right.$$

(54)

where c_s1 and c_s2 are the compliance coefficients along the x-axis of subassembly elements 1 and 2, respectively.

The stiffness coefficients of the subassembly elements can be obtained using Eq. (6).

$$\left\{ \begin{gathered} k_{s1} = \frac{{k_{1} k_{{{\text{J}}1}} }}{{k_{1} + k_{{{\text{J}}1}} }}, \hfill \\ k_{s2} = \frac{{k_{2} k_{{{\text{J2}}}} }}{{k_{2} + k_{{{\text{J2}}}} }}. \hfill \\ \end{gathered} \right.$$

(55)

When the elastic joints are considered rigid, the compliance coefficients of the subassembly elements in Eq. (55) are consistent with those of the beam elements. Therefore, the subassembly stiffness coefficients obtained using Eq. (55) are consistent with those of the beam elements. The effectively eliminates the singularity problem expressed in Eq. (48), thereby avoiding the numerical instability inherent in the traditional method (Figure 5).

4 Case Study 2: Over Constrained Delta PM With Over-Constrained Subclosed Loops

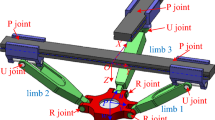
The over-constrained delta PM with over-constrained subclosed loops, as shown in Figure 6, serves as an example for implementing the proposed method. This mechanism employs only revolute joints to constrain the output of the moving platform from translational motion. The moving platform was connected to the fixed base by three identical limbs, each consisting of a lower arm and an upper arm constructed as an over constrained planar four-bar parallelogram. The lower arm A_iB_i is labeled as link i1, and each upper arm is sequentially labeled as links i2, i3, and i4. The coordinate frames are defined as follows: the global coordinate frame O-xyz is attached to the center O, with its y-axis along OA₁ and its z-axis pointing vertically upward; element coordinate frames {B_i} and {C_i} with their x-axis aligned along B_i1B_i2 and their z-axis aligned along A_iB_i; element coordinate frames {B_i1} and {B_i2} with their z-axis aligned along B_i1C_i1 and their y-axis points aligned along the axis of revolution of the parallelogram. The joint coordinate frame was consistent with its subassembly element coordinate frame.

Figure 6

Over-constrained delta PM with over-constrained subclosed loops

4.1 Elastostatic Stiffness Model of the Delta PM

According to the procedure outlined for the proposed elastostatic stiffness model described in Section 2, the first step involved cutting open the closed-loop delta PM at the joints and converting it into an open-loop mechanism. The manipulator is then discretized into the following subassembly elements: R-joint at A_i and link A_iB_i; R-joint at B_i and link B_i1B_i2; R-joint at B_i1, R-joint at C_i1, and link B_i1C_i1; R-joint at B_i2, R-joint at C_i2, and link B_i2C_i2; R-joint at C_i and link C_i1C_i2; a rigid moving platform; and a rigid base. The resulting open loops of the delta PM are shown in Figure 7.

Figure 7

Open-loops of the delta PM

To clearly present the proposed method, each link is discretized into one element, except for link B_i1B_i2. The static model of the subassembly element A_iB_i in the element coordinate frame is then provided.

$${}^{\text{s}}{\varvec{K}}_{i1} \left[ {\begin{array}{*{20}c} {{}^{\text{s}}{{\varvec{\Delta}}}_{i1} } \\ {{}^{\text{s}}{{\varvec{\Delta}}}_{i2} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {{}^{\text{s}}{\varvec{W}}_{i1} } \\ {{}^{\text{s}}{\varvec{W}}_{i2} } \\ \end{array} } \right],$$

(56)

where Δ_ij and W_ij are the displacement column vector and force column vector of the jth node of the ith element, respectively.

Eq. (56) can be further expressed in global coordinates according to the rotation matrix as follows:

$${\varvec{K}}_{i1} \left[ {\begin{array}{*{20}c} {{{\varvec{\Delta}}}_{i1} } \\ {{{\varvec{\Delta}}}_{i2} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {{\varvec{W}}_{i1} } \\ {{\varvec{W}}_{i2} } \\ \end{array} } \right],$$

(57)

where ${\varvec{K}}_{ij} = {\varvec{T}}_{ij}^{{}} {}^{s}{\varvec{K}}_{ij} {\varvec{T}}_{ij}^{{\text{T}}}$ (j = 1, 2, 4), ${\varvec{T}}_{ij}^{{}} = \text{diag}({\varvec{R}}_{ij}^{{}} ,\;{\varvec{R}}_{ij}^{{}} ,\;{\varvec{R}}_{ij}^{{}} ,\;{\varvec{R}}_{ij}^{{}} )$, R_ij are the rotation matrices from the jth element coordinate frame of the ith limb to the global coordinate frame.

Similarly, a static model of the subassembly elements B_i1C_i1 and B_i2C_i2 can was obtained.

Notably, the subassembly B_i1B_i2 is discretized into three nodes, B_i1, B_i, and B_i2 to present the constraint relationship between subassemblies A_iB_i and B_i1B_i2. A beam element model that can rotate around its axis was considered to model the subassembly B_i1B_i2. The element stiffness matrix of subassembly B_i1B_i2 can be expressed as follows:

$$\left\{ \begin{gathered} {}^{s}{\varvec{K}}_{{i2}} = \left[ {\begin{array}{*{20}c} {{\varvec{K}}_{{i2,e1,11}} } & {{\varvec{K}}_{{i2,e1,12}} } & {{\varvec{0}}_{{6 \times 6}} } \\ {{\varvec{K}}_{{i2,e1,21}} } & {{\varvec{K}}_{{i2,e1,22}} + {\varvec{K}}_{{i2,e2,11}} } & {{\varvec{K}}_{{i2,e2,12}} } \\ {{\varvec{0}}_{{6 \times 6}} } & {{\varvec{K}}_{{i2,e2,21}} } & {{\varvec{K}}_{{i2,e2,22}} } \\ \end{array} } \right], \hfill \\ {\varvec{K}}_{{i2}} = {\varvec{T}}_{{i2}}^{{\text{T}}} {}^{s}{\varvec{K}}_{{i2}} {\varvec{T}}_{{i2}}^{{}} \;\left( {{\varvec{T}}_{{i2}}^{{}} = {\text{diag}}[{\varvec{R}}_{{i2}}^{{}} ,\;{\varvec{R}}_{{i2}}^{{}} ,\;{\varvec{R}}_{{i2}}^{{}} ,\;{\varvec{R}}_{{i2}}^{{}} ,\;{\varvec{R}}_{{i2}}^{{}} ,\;{\varvec{R}}_{{i2}}^{{}} ]} \right), \hfill \\ \end{gathered} \right.$$

(58)

Similarly, the stiffness matrix of the subassembly C_i1C_i2 can thus be obtained.

The second step involved extracting the IDCs of the boundary nodes according to the method presented in Section 2.2. For a delta PM, the IDCs of the boundary nodes connected to the revolute joint can be obtained using Eq. (24) and Appendix.

Finally, the open-loop mechanism was closed by establishing a mapping equation from the non-independent displacement coordinates of each free body to the global IDCs of the mechanism. According to the introduction in Section 2.3, the global IDCs of the delta PM are given by:

$$\begin{gathered} U = [\varphi_{12x} ,\;{\varvec{u}}_{13} ,\;{\varvec{u}}_{14} ,\;{\varvec{u}}_{15} ,\;\varphi_{16y} ,\;\varphi_{17y} ,\;\varphi_{18y} ,\;\varphi_{19y} ,\;{\varvec{u}}_{110} ,\;\; \hfill \\ \quad \quad \varphi_{111x} ,{\varvec{u}}_{112} ,\; \ldots \;,\varphi_{32x} ,\;{\varvec{u}}_{33} ,\;{\varvec{u}}_{34} ,\;{\varvec{u}}_{35} ,\;\varphi_{36y} ,\;\varphi_{37y},\;\; \hfill \\ \quad \quad\varphi_{38y} ,\;\varphi_{39y} {\varvec{u}}_{310} ,\;\varphi_{311x} ,\;{\varvec{u}}_{312} ,\; \ldots \;,{\varvec{u}}_{p} ]. \hfill \\ \end{gathered}$$

(59)

Accordingly, referring to Appendix, the mapping matrix H_ij between the element displacement column vector of the free body and global IDCs can be obtained as follows:

$$\left\{ \begin{gathered} {\varvec{H}}_{11} = \left[ {\begin{array}{*{20}c} {{\varvec{0}}_{6 \times 114} } & {} & {} & {} \\ {{\varvec{0}}_{3 \times 7} } & {{\varvec{E}}_{3} } & {{\varvec{0}}_{3 \times 104} } & {} \\ 1 & {{\varvec{0}}_{1 \times 113} } & {} & {} \\ {r_{12,21} } & {{\varvec{0}}_{1 \times 9} } & {{\varvec{a}}_{1,2y} - r_{12,21} {\varvec{a}}_{1,2x} } & {{\varvec{0}}_{1 \times 101} } \\ {r_{12,31} } & {{\varvec{0}}_{1 \times 9} } & {{\varvec{a}}_{1,2z} - r_{12,31} {\varvec{a}}_{1,2x} } & {{\varvec{0}}_{1 \times 101} } \\ \end{array} } \right], \hfill \\ {\varvec{H}}_{21} = \left[ {\begin{array}{*{20}c} {{\varvec{0}}_{6 \times 114} } & {} & {} & {} & {} \\ {{\varvec{0}}_{3 \times 43} } & {{\varvec{E}}_{3} } & {{\varvec{0}}_{3 \times 68} } & {} & {} \\ {{\varvec{0}}_{1 \times 36} } & 1 & {{\varvec{0}}_{1 \times 77} } & {} & {} \\ {{\varvec{0}}_{1 \times 36} } & {r_{22,21} } & {{\varvec{0}}_{1 \times 9} } & {{\varvec{a}}_{2,2y} - r_{22,21} {\varvec{a}}_{2,2x} } & {{\varvec{0}}_{1 \times 65} } \\ {{\varvec{0}}_{1 \times 36} } & {r_{22,31} } & {{\varvec{0}}_{1 \times 9} } & {{\varvec{a}}_{2,2z} - r_{22,31} {\varvec{a}}_{2,2x} } & {{\varvec{0}}_{1 \times 65} } \\ \end{array} } \right], \hfill \\ {\varvec{H}}_{31} = \left[ {\begin{array}{*{20}c} {{\varvec{0}}_{6 \times 114} } & {} & {} & {} & {} \\ {{\varvec{0}}_{3 \times 79} } & {{\varvec{E}}_{3} } & {{\varvec{0}}_{3 \times 32} } & {} & {} \\ {{\varvec{0}}_{1 \times 72} } & 1 & {{\varvec{0}}_{1 \times 41} } & {} & {} \\ {{\varvec{0}}_{1 \times 72} } & {r_{32,21} } & {{\varvec{0}}_{1 \times 9} } & {{\varvec{a}}_{3,2y} - r_{32,21} {\varvec{a}}_{3,2x} } & {{\varvec{0}}_{1 \times 29} } \\ {{\varvec{0}}_{1 \times 72} } & {r_{32,31} } & {{\varvec{0}}_{1 \times 9} } & {{\varvec{a}}_{3,2z} - r_{32,31} {\varvec{a}}_{3,2x} } & {{\varvec{0}}_{1 \times 29} } \\ \end{array} } \right] ,\hfill \\ \end{gathered} \right.\;$$

(60)

where $r_{i2,21} = \frac{{R_{i1} (2,1)}}{{R_{i1} (1,1)}}$,$r_{i2,31} = \frac{{R_{i1} (3,1)}}{{R_{i1} (1,1)}}$,${\varvec{a}}_{i,2x} = R_{i1} (1,2){\varvec{Q}}_{i2} (1,:) + R_{i1} (1,3){\varvec{Q}}_{i2} (2,:)$,${\varvec{a}}_{i,2y} = R_{i1} (2,2){\varvec{Q}}_{i1} (1,:) + R_{i1} (2,3){\varvec{Q}}_{i1} (2,:)$,${\varvec{a}}_{i,2z} = R_{i1} (3,2){\varvec{Q}}_{i1} (1,:) + R_{i1} (3,3){\varvec{Q}}_{i1} (2,:)$,${\varvec{Q}}_{i1} = \left[ {\begin{array}{*{20}c} 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{array} } \right]{\varvec{R}}_{i1}^{{\text{T}}}$.

$$\left\{ \begin{gathered} {\varvec{H}}_{12} = \left[ {\begin{array}{*{20}c} {{\varvec{0}}_{6 \times 1} } & {{\varvec{E}}_{6} } & {{\varvec{0}}_{6 \times 107} } \\ {{\varvec{0}}_{6 \times 7} } & {{\varvec{E}}_{6} } & {{\varvec{0}}_{6 \times 101} } \\ {{\varvec{0}}_{6 \times 13} } & {{\varvec{E}}_{6} } & {{\varvec{0}}_{6 \times 95} } \\ \end{array} } \right],\hfill \\\;{\varvec{H}}_{22} = \left[ {\begin{array}{*{20}c} {{\varvec{0}}_{6 \times 37} } & {{\varvec{E}}_{6} } & {{\varvec{0}}_{6 \times 71} } \\ {{\varvec{0}}_{6 \times 43} } & {{\varvec{E}}_{6} } & {{\varvec{0}}_{6 \times 65} } \\ {{\varvec{0}}_{6 \times 49} } & {{\varvec{E}}_{6} } & {{\varvec{0}}_{6 \times 59} } \\ \end{array} } \right], \hfill \\ {\varvec{H}}_{32} = \left[ {\begin{array}{*{20}c} {{\varvec{0}}_{6 \times 73} } & {{\varvec{E}}_{6} } & {{\varvec{0}}_{6 \times 35} } \\ {{\varvec{0}}_{6 \times 79} } & {{\varvec{E}}_{6} } & {{\varvec{0}}_{6 \times 29} } \\ {{\varvec{0}}_{6 \times 85} } & {{\varvec{E}}_{6} } & {{\varvec{0}}_{6 \times 23} } \\ \end{array} } \right], \hfill \\ \end{gathered} \right.\;$$

(61)

$$\left\{ \begin{gathered} {\varvec{H}}_{13} = \left[ {\begin{array}{*{20}c} {{\varvec{0}}_{3 \times 1} } & {{\varvec{E}}_{3} } & {{\varvec{0}}_{3 \times 110} } & {} & {} \\ {{\varvec{0}}_{1 \times 4} } & {{\varvec{a}}_{1,3x} - r_{13,12} {\varvec{a}}_{1,3y} } & {{\varvec{0}}_{1 \times 12} } & {r_{13,12} } & {{\varvec{0}}_{1 \times 94} } \\ {{\varvec{0}}_{1 \times 9} } & 1 & {{\varvec{0}}_{1 \times 94} } & {} & {} \\ {{\varvec{0}}_{1 \times 4} } & {{\varvec{a}}_{1,3z} - r_{13,32} {\varvec{a}}_{1,3y} } & {{\varvec{0}}_{1 \times 12} } & {r_{13,32} } & {{\varvec{0}}_{1 \times 94} } \\ {{\varvec{0}}_{3 \times 23} } & {{\varvec{E}}_{3} } & {{\varvec{0}}_{3 \times 88} } & {} & {} \\ {{\varvec{0}}_{1 \times 20} } & {r_{13,12} } & {{\varvec{0}}_{1 \times 5} } & {{\varvec{a}}_{1,3x} - r_{13,12} {\varvec{a}}_{1,3y} } & {{\varvec{0}}_{1 \times 85} } \\ {{\varvec{0}}_{1 \times 20} } & 1 & {{\varvec{0}}_{1 \times 93} } & {} & {} \\ {{\varvec{0}}_{1 \times 20} } & {r_{13,32} } & {{\varvec{0}}_{1 \times 5} } & {{\varvec{a}}_{1,3z} - r_{13,32} {\varvec{a}}_{1,3y} } & {{\varvec{0}}_{1 \times 85} } \\ \end{array} } \right], \hfill \\ {\varvec{H}}_{23} = \left[ {\begin{array}{*{20}c} {{\varvec{0}}_{3 \times 37} } & {{\varvec{E}}_{3} } & {{\varvec{0}}_{3 \times 74} } & {} & {} \\ {{\varvec{0}}_{1 \times 40} } & {{\varvec{a}}_{2,3x} - r_{23,12} {\varvec{a}}_{2,3y} } & {{\varvec{0}}_{1 \times 12} } & {r_{23,12} } & {{\varvec{0}}_{1 \times 58} } \\ {{\varvec{0}}_{1 \times 55} } & 1 & {{\varvec{0}}_{1 \times 58} } & {} & {} \\ {{\varvec{0}}_{1 \times 40} } & {{\varvec{a}}_{2,3z} - r_{23,32} {\varvec{a}}_{2,3y} } & {{\varvec{0}}_{1 \times 12} } & {r_{23,32} } & {{\varvec{0}}_{1 \times 58} } \\ {{\varvec{0}}_{3 \times 59} } & {{\varvec{E}}_{3} } & {{\varvec{0}}_{3 \times 52} } & {} & {} \\ {{\varvec{0}}_{1 \times 56} } & {r_{23,12} } & {{\varvec{0}}_{1 \times 5} } & {{\varvec{a}}_{2,3x} - r_{23,12} {\varvec{a}}_{2,3y} } & {{\varvec{0}}_{1 \times 49} } \\ {{\varvec{0}}_{1 \times 56} } & 1 & {{\varvec{0}}_{1 \times 57} } & {} & {} \\ {{\varvec{0}}_{1 \times 56} } & {r_{23,32} } & {{\varvec{0}}_{1 \times 5} } & {{\varvec{a}}_{2,3z} - r_{23,32} {\varvec{a}}_{2,3y} } & {{\varvec{0}}_{1 \times 49} } \\ \end{array} } \right], \hfill \\ {\varvec{H}}_{33} = \left[ {\begin{array}{*{20}c} {{\varvec{0}}_{3 \times 73} } & {{\varvec{E}}_{3} } & {{\varvec{0}}_{3 \times 38} } & {} & {} \\ {{\varvec{0}}_{1 \times 76} } & {{\varvec{a}}_{3,3x} - r_{33,12} {\varvec{a}}_{3,3y} } & {{\varvec{0}}_{1 \times 12} } & {r_{33,12} } & {{\varvec{0}}_{1 \times 22} } \\ {{\varvec{0}}_{1 \times 91} } & 1 & {{\varvec{0}}_{1 \times 22} } & {} & {} \\ {{\varvec{0}}_{1 \times 76} } & {{\varvec{a}}_{3,3z} - r_{33,32} {\varvec{a}}_{3,3y} } & {{\varvec{0}}_{1 \times 12} } & {r_{33,32} } & {{\varvec{0}}_{1 \times 22} } \\ {{\varvec{0}}_{3 \times 95} } & {{\varvec{E}}_{3} } & {{\varvec{0}}_{3 \times 16} } & {} & {} \\ {{\varvec{0}}_{1 \times 92} } & {r_{33,12} } & {{\varvec{0}}_{1 \times 5} } & {{\varvec{a}}_{3,3x} - r_{33,12} {\varvec{a}}_{3,3y} } & {{\varvec{0}}_{1 \times 13} } \\ {{\varvec{0}}_{1 \times 92} } & 1 & {{\varvec{0}}_{1 \times 21} } & {} & {} \\ {{\varvec{0}}_{1 \times 92} } & {r_{33,32} } & {{\varvec{0}}_{1 \times 5} } & {{\varvec{a}}_{3,3z} - r_{33,32} {\varvec{a}}_{3,3y} } & {{\varvec{0}}_{1 \times 13} } \\ \end{array} } \right], \hfill \\ \end{gathered} \right.\;$$

(62)

where $r_{i3,12} = \frac{{R_{i3} (1,2)}}{{R_{i3} (2,2)}}$,$r_{i3,32} = \frac{{R_{i3} (3,2)}}{{R_{i3} (2,2)}}$.${\varvec{a}}_{i,3x} = R_{i3} (1,1){\varvec{Q}}_{i3} (1,:) + R_{i3} (1,3){\varvec{Q}}_{i3} (2,:)$,${\varvec{a}}_{i,3y} = R_{i3} (2,1){\varvec{Q}}_{i3} (1,:) + R_{i3} (2,3){\varvec{Q}}_{i3} (2,:)$,${\varvec{a}}_{i,3z} = R_{i3} (3,1){\varvec{Q}}_{i3} (1,:) + R_{i3} (3,3){\varvec{Q}}_{i2} (2,:)$,${\varvec{Q}}_{i3} = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & 0 & 1 \\ \end{array} } \right]{\varvec{R}}_{i3}^{{\text{T}}}$.

The presented examples in this section highlight that the proposed stiffness model lie in the ease with which designers can swiftly assemble the overall stiffness matrix of the PM. By referring to the Appendix provided in this paper, designers can avoid complicated mathematical operations, thereby greatly improving the efficiency of stiffness modeling.

$$\left\{ \begin{gathered} {\varvec{H}}_{14} = \left[ {\begin{array}{*{20}c} {{\varvec{0}}_{3 \times 13} } & {{\varvec{E}}_{3} } & {{\varvec{0}}_{3 \times 98} } & {} & {} \\ {{\varvec{0}}_{1 \times 16} } & {{\varvec{a}}_{1,3x} - r_{13,12} {\varvec{a}}_{1,3y} } & {{\varvec{0}}_{1 \times 2} } & {r_{13,12} } & {{\varvec{0}}_{1 \times 92} } \\ {{\varvec{0}}_{1 \times 21} } & 1 & {{\varvec{0}}_{1 \times 92} } & {} & {} \\ {{\varvec{0}}_{1 \times 16} } & {{\varvec{a}}_{1,3z} - r_{13,32} {\varvec{a}}_{1,3y} } & {{\varvec{0}}_{1 \times 2} } & {r_{13,32} } & {{\varvec{0}}_{1 \times 92} } \\ {{\varvec{0}}_{3 \times 30} } & {{\varvec{E}}_{3} } & {{\varvec{0}}_{3 \times 81} } & {} & {} \\ {{\varvec{0}}_{1 \times 22} } & {r_{13,12} } & {{\varvec{0}}_{1 \times 10} } & {{\varvec{a}}_{1,3x} - r_{13,12} {\varvec{a}}_{1,3y} } & {{\varvec{0}}_{1 \times 78} } \\ {{\varvec{0}}_{1 \times 22} } & 1 & {{\varvec{0}}_{1 \times 91} } & {} & {} \\ {{\varvec{0}}_{1 \times 22} } & {r_{13,32} } & {{\varvec{0}}_{1 \times 10} } & {{\varvec{a}}_{1,3z} - r_{13,32} {\varvec{a}}_{1,3y} } & {{\varvec{0}}_{1 \times 78} } \\ \end{array} } \right], \hfill \\ {\varvec{H}}_{24} = \left[ {\begin{array}{*{20}c} {{\varvec{0}}_{3 \times 49} } & {{\varvec{E}}_{3} } & {{\varvec{0}}_{3 \times 62} } & {} & {} \\ {{\varvec{0}}_{1 \times 52} } & {{\varvec{a}}_{2,3x} - r_{23,12} {\varvec{a}}_{2,3y} } & {{\varvec{0}}_{1 \times 2} } & {r_{23,12} } & {{\varvec{0}}_{1 \times 56} } \\ {{\varvec{0}}_{1 \times 57} } & 1 & {{\varvec{0}}_{1 \times 56} } & {} & {} \\ {{\varvec{0}}_{1 \times 52} } & {{\varvec{a}}_{2,3z} - r_{23,32} {\varvec{a}}_{2,3y} } & {{\varvec{0}}_{1 \times 2} } & {r_{23,32} } & {{\varvec{0}}_{1 \times 56} } \\ {{\varvec{0}}_{3 \times 66} } & {{\varvec{E}}_{3} } & {{\varvec{0}}_{3 \times 45} } & {} & {} \\ {{\varvec{0}}_{1 \times 58} } & {r_{23,12} } & {{\varvec{0}}_{1 \times 10} } & {{\varvec{a}}_{2,3x} - r_{23,12} {\varvec{a}}_{2,3y} } & {{\varvec{0}}_{1 \times 42} } \\ {{\varvec{0}}_{1 \times 58} } & 1 & {{\varvec{0}}_{1 \times 55} } & {} & {} \\ {{\varvec{0}}_{1 \times 58} } & {r_{23,32} } & {{\varvec{0}}_{1 \times 10} } & {{\varvec{a}}_{2,3z} - r_{23,32} {\varvec{a}}_{2,3y} } & {{\varvec{0}}_{1 \times 42} } \\ \end{array} } \right], \hfill \\ {\varvec{H}}_{34} = \left[ {\begin{array}{*{20}c} {{\varvec{0}}_{3 \times 85} } & {{\varvec{E}}_{3} } & {{\varvec{0}}_{3 \times 26} } & {} & {} \\ {{\varvec{0}}_{1 \times 88} } & {{\varvec{a}}_{3,3x} - r_{33,12} {\varvec{a}}_{3,3y} } & {{\varvec{0}}_{1 \times 2} } & {r_{33,12} } & {{\varvec{0}}_{1 \times 20} } \\ {{\varvec{0}}_{1 \times 93} } & 1 & {{\varvec{0}}_{1 \times 20} } & {} & {} \\ {{\varvec{0}}_{1 \times 88} } & {{\varvec{a}}_{3,3z} - r_{33,32} {\varvec{a}}_{3,3y} } & {{\varvec{0}}_{1 \times 2} } & {r_{33,32} } & {{\varvec{0}}_{1 \times 20} } \\ {{\varvec{0}}_{3 \times 102} } & {{\varvec{E}}_{3} } & {{\varvec{0}}_{3 \times 9} } & {} & {} \\ {{\varvec{0}}_{1 \times 94} } & {r_{33,12} } & {{\varvec{0}}_{1 \times 10} } & {{\varvec{a}}_{3,3x} - r_{33,12} {\varvec{a}}_{3,3y} } & {{\varvec{0}}_{1 \times 6} } \\ {{\varvec{0}}_{1 \times 94} } & 1 & {{\varvec{0}}_{1 \times 19} } & {} & {} \\ {{\varvec{0}}_{1 \times 94} } & {r_{33,32} } & {{\varvec{0}}_{1 \times 10} } & {{\varvec{a}}_{3,3z} - r_{33,32} {\varvec{a}}_{3,3y} } & {{\varvec{0}}_{1 \times 6} } \\ \end{array} } \right], \hfill \\ \end{gathered} \right.$$

(63)

$$\left\{ \begin{gathered} {\varvec{H}}_{15} = \left[ {\begin{array}{*{20}c} {{\varvec{0}}_{6 \times 23} } & {{\varvec{E}}_{6} } & {{\varvec{0}}_{6 \times 85} } & {} \\ {{\varvec{0}}_{3 \times 108} } & {{\varvec{J}}_{c1} } & {} & {} \\ {{\varvec{0}}_{1 \times 29} } & 1 & {{\varvec{0}}_{1 \times 84} } & {} \\ {{\varvec{0}}_{1 \times 29} } & {r_{12,21} } & {{\varvec{0}}_{1 \times 81} } & {{\varvec{a}}_{1,2y} - r_{12,21} {\varvec{a}}_{1,2x} } \\ {{\varvec{0}}_{1 \times 29} } & {r_{12,31} } & {{\varvec{0}}_{1 \times 81} } & {{\varvec{a}}_{1,2z} - r_{12,31} {\varvec{a}}_{1,2x} } \\ {{\varvec{0}}_{6 \times 30} } & {{\varvec{E}}_{6} } & {{\varvec{0}}_{6 \times 78} } & {} \\ \end{array} } \right], \hfill \\ \;{\varvec{H}}_{25} = \left[ {\begin{array}{*{20}c} {{\varvec{0}}_{6 \times 59} } & {{\varvec{E}}_{6} } & {{\varvec{0}}_{6 \times 49} } & {} \\ {{\varvec{0}}_{3 \times 108} } & {{\varvec{J}}_{c2} } & {} & {} \\ {{\varvec{0}}_{1 \times 65} } & 1 & {{\varvec{0}}_{1 \times 48} } & {} \\ {{\varvec{0}}_{1 \times 65} } & {r_{22,21} } & {{\varvec{0}}_{1 \times 45} } & {{\varvec{a}}_{2,2y} - r_{22,21} {\varvec{a}}_{2,2x} } \\ {{\varvec{0}}_{1 \times 65} } & {r_{22,31} } & {{\varvec{0}}_{1 \times 45} } & {{\varvec{a}}_{2,2z} - r_{22,31} {\varvec{a}}_{2,2x} } \\ {{\varvec{0}}_{6 \times 66} } & {{\varvec{E}}_{6} } & {{\varvec{0}}_{6 \times 42} } & {} \\ \end{array} } \right], \hfill \\ {\varvec{H}}_{35} = \left[ {\begin{array}{*{20}c} {{\varvec{0}}_{6 \times 95} } & {{\varvec{E}}_{6} } & {{\varvec{0}}_{6 \times 13} } & {} \\ {{\varvec{0}}_{3 \times 108} } & {{\varvec{J}}_{c3} } & {} & {} \\ {{\varvec{0}}_{1 \times 101} } & 1 & {{\varvec{0}}_{1 \times 12} } & {} \\ {{\varvec{0}}_{1 \times 101} } & {r_{32,21} } & {{\varvec{0}}_{1 \times 9} } & {{\varvec{a}}_{3,2y} - r_{32,21} {\varvec{a}}_{3,2x} } \\ {{\varvec{0}}_{1 \times 101} } & {r_{32,31} } & {{\varvec{0}}_{1 \times 9} } & {{\varvec{a}}_{3,2z} - r_{32,31} {\varvec{a}}_{3,2x} } \\ {{\varvec{0}}_{6 \times 102} } & {{\varvec{E}}_{6} } & {{\varvec{0}}_{6 \times 6} } & {} \\ \end{array} } \right]. \hfill \\ \end{gathered} \right.$$

(64)

The commercial ANSYS Workbench software was used to verify the accuracy of the proposed model. A line body with a circular cross section was adopted to improve the computational cost of the FEM. The flexible joint is modeled using a bush element that can simulate the stiffness and damping of the joints in six directions (three translations and three rotations). We consider the comparison of deformation results of the output point of the manipulator under a predefined trajectory (Figure 8) and a given random general external load [15] W = [-20 N, 10 N, 100 N, 5 N·m, 5 N·m, 8 N·m] to verify the correctness of the proposed model.

$$\left\{ \begin{gathered} x = - 0.2,\;y = - 0.2,\;z = 0.45 + 0.05t\;\;(0 \le t \le 2),\; \hfill \\ x = - 0.2 + 0.2(t - 2),\;y = - 0.2,\;z = 0.55\;\;(2 \le t \le 4),\; \hfill \\ x = 0.2,\;y = - 0.2,\;z = 0.55 - 0.05(t - 4)\;\;(4 \le t \le 6).\; \hfill \\ \end{gathered} \right.\;$$

(65)

Figure 8

Comparison of the deformed trajectory from the proposed method and ANSYS software

The calculation results obtained based on the proposed method are consistent with those of commercial ANSYS software, and the maximum error is within 1.05%, which verifies the accuracy of the proposed method.

Figure 9 shows the undeformed and deformed results of the delta PM obtained using MATLAB and ANSYS software. The maximum error was less than 0.94%, which further proves the accuracy of the proposed modeling. Notably, due to the extraction of non-singular global IDCs in this study, simultaneous constraint equations become unnecessary in the static model. This reduction significantly decreases computational costs to 0.0017 s on a desk computer with a Core i5-8500 CPU@ 3.00 GHz. In contrast, the ANSYS model requires 2 s for computation. Therefore, the proposed model achieves a remarkable 99.15% reduction in computational cost while maintain accuracy.

Figure 9

Comparison of the deformed delta PM from the proposed method and ANSYS software

4.2 Compared With the Existing Methods

The traditional method for handling the kinematic constraint of a structure considers the elastic joint as a spring [11] and establishes a mapping equation between the spring wrench (constraint wrench) and the deformation difference between the two connected nodes.

$${\varvec{W}}_{{\text{J}}} = {\varvec{K}}_{{\text{J}}} ({\varvec{u}}_{1} - {\varvec{u}}_{2} ),$$

(66)

where W_J is the constraint wrenches acting on the flexibility joint.

The constraints in Eq. (66) are combined with MSA technology and the Lagrangian equation [20] to establish static modeling (the detailed derivation process of the delta mechanism based on this method can be found in Ref. [20]). The limitations of this method are threefold. (i) computational inefficiency because of the requirement of additional Lagrangian multipliers. The energy equation needs to be derived separately for different structures, making it unsuitable for engineering applications; (ii) when the flexibility joint degenerates to become rigid, Eq. (66) becomes singular and numerical calculations become unstable. This issue has been discussed in detail in Section 3; (iii) similar to (ii), due to the inverse operation of the matrix K_J being required, the true zero stiffness value in the direction of the free relative DOF needs to be replaced by a value close to zero to avoid causing instability in numerical calculations. For example, Deblaise et al. [20] chose the axial rotational stiffness of a revolute joint to 10^-7 N·rad^-1 to avoid numerical instability. This renders them inconsistent with the engineering environment and obscures their physical meaning.

Another classical model is the finite-element method. In commercial software like ANSYS, U-joint constraint is exemplified, and the rotation constraint is expressed as

$${\varvec{x}}^{i} \cdot {\varvec{y}}^{j} = 0,$$

(67)

where xⁱ and y^j are the column vectors of nodes i and j, respectively, in the joint space.

In commercial finite element software like ANSYS, U-joint constraints are applied by determining the perpendicular relationship between the U-joint axes of two overlapping nodes. During the static modeling process, verifying whether the constraint equations were violated is necessary. However, sometimes the independent angular displacement coordinates are not successfully separated, which hampers the rapid assembly of the overall static equation of the structure, thus not maximizing the efficiency of element assembly and calculation. The constraint equations for the other joints are similar to those for the U-joint, and more details can be found in the ANSYS help document.

5 Conclusions

Establishing an elastostatic stiffness model of a multi-joint and multi-object over constrained system with over constrained subsystems poses a significant challenge owing to its complex constraint equations. Traditionally, because the global IDCs of such structures are not readily available in the global coordinate frame, and the flexibility joint constraint is often treated as a spring constraint, simultaneous constraint equations or additional Lagrangian multipliers are required in modeling methods. However, this approach can lead to numerical instability and computational inefficiency. In this paper, a systematic elastostatic stiffness model of PMs is proposed based on MSA, subassembly element stiffness matrix, and IDCs. The main advantages of this model are as follows: (1) The method is modeling efficient because of the non-singular constraint equations for various joints encountered in engineering, as presented in Appendix. The elastostatic stiffness model can be quickly established by combining the rotation matrices between coordinate frames. (2) The proposed model is computationally efficient because the constraint equations are presented in the analytical expression in the global coordinate, and simultaneous constraint and Lagrangian multipliers are not required. (3) The proposed model is numerically stable because the zero-stiffness component can be considered in the direction of the free relative DOF.

An over-constrained delta PM with three over-constrained subclosed loops serves as an example to implement the proposed method. Comparison with ANSYS software results showed that a maximum error of loss than 1.05% for the specified trajectory and within 0.94% for mechanism deformation. However, the computational cost of the proposed method was reduced by 99.15%, confirming its accuracy and effectiveness. To the best of the authors’ knowledge, this study represents the first systematic study on the extraction technology of IDCs connected by various joints in a global coordinate system. The proposed method provides a solution for the elastostatic stiffness model of complex over-constrained PMs.

Appendix

IDCs of nodes connected by various joints often encountered in engineering

Constraints	IDCs and constraint equations	Notes
Universal Joint	uJ = [Δi, φi, Δj, φj], ${\varvec{u}}_{U,id} = \left[ {\varphi_{ix} \;\varphi_{iy} \;{\varvec{u}}_{j} } \right]$, ${\varvec{u}}_{J} = \left[ {\begin{array}{*{20}c} {{\varvec{0}}_{3 \times 2} } & {{\varvec{E}}_{3} } & {{\varvec{0}}_{3} } & {} \\ 1 & {{\varvec{0}}_{1 \times 7} } & {} & {} \\ 0 & 1 & {{\varvec{0}}_{1 \times 6} } & {} \\ {a_{Uix} } & {a_{Uiy} } & {{\varvec{0}}_{1 \times 3} } & {a_{Uip} {\varvec{Q}}_{U} } \\ {{\varvec{0}}_{6 \times 2} } & {{\varvec{E}}_{6} } & {} & {} \\ \end{array} } \right]{\varvec{u}}_{U,id}$.	$a_{Uix} = \frac{{R_{U} (3,1)R_{U} (2,2) - R_{U} (3,2)R_{U} (2,1)}}{{R_{U} (1,1)R_{U} (2,2) - R_{U} (1,2)R_{U} (2,1)}}$, $a_{{{\text{U}}iy}} = \frac{{R_{U} (1,1)R_{U} (3,2) - R_{U} (1,2)R_{U} (3,1)}}{{R_{U} (1,1)R_{U} (2,2) - R_{U} (1,2)R_{U} (2,1)}}$, QU = [0 0 1]RU -1, $a_{{{\text{U}}ip}} = [R_{U} (3,2)(R_{U} (1,3)R_{U} (2,1) - R_{U} (1,1)R_{U} (2,3))$$- R_{U} (3,1)(R_{U} (1,3)R_{U} (2,2) - R_{U} (1,2)R_{U} (2,3))]$/$[R_{U} (1,1)R_{U} (2,2) - R_{U} (1,2)R_{U} (2,1)]$$+ R_{U} (3,3)$.
Revolute joint	${\varvec{u}}_{R,id} = \left[ {\varphi_{iy} \;{\varvec{u}}_{j} } \right]$, ${\varvec{u}}_{J} = \left[ {\begin{array}{*{20}c} {{\varvec{0}}_{3 \times 1} } & {{\varvec{E}}_{3} } & {{\varvec{0}}_{3} } \\ {\frac{{R_{R} (1,2)}}{{R_{R} (2,2)}}} & {{\varvec{0}}_{1 \times 3} } & {{\varvec{a}}_{Rix} - \frac{{R_{R} (1,2){\varvec{a}}_{Riy} }}{{R_{R} (2,2)}}} \\ 1 & {{\varvec{0}}_{1 \times 6} } & {} \\ {\frac{{R_{R} (3,2)}}{{R_{R} (2,2)}}} & {{\varvec{0}}_{1 \times 3} } & {{\varvec{a}}_{Riz} - \frac{{R_{R} (3,2){\varvec{a}}_{iy} }}{{R_{R} (2,2)}}} \\ {{\varvec{0}}_{6 \times 1} } & {{\varvec{E}}_{6} } & {} \\ \end{array} } \right]{\varvec{u}}_{R,id}$.	${\varvec{a}}_{{{\text{R}}ix}} = R_{R} (1,1){\varvec{Q}}_{R} (1,:) + R_{R} (1,3){\varvec{Q}}_{R} (2,:)$, ${\varvec{a}}_{{{\text{R}}iy}} = R_{R} (2,1){\varvec{Q}}_{R} (1,:) + R_{R} (2,3){\varvec{Q}}_{R} (2,:)$, ${\varvec{a}}_{{{\text{R}}iz}} = R_{R} (3,1){\varvec{Q}}_{R} (1,:) + R_{R} (3,3){\varvec{Q}}_{R} (2,:)$, ${\varvec{Q}}_{R}\, =\,\left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & 0 & 1 \\ \end{array} } \right]{\varvec{R}}_{R}^{ - 1}$.
	${\varvec{u}}_{S,id} = \left[ {\varphi_{ix} \;\varphi_{iy} \;\varphi_{iz} \;{\varvec{u}}_{j} } \right]$, ${\varvec{u}}_{J} = \left[ {\begin{array}{*{20}c} {{\varvec{0}}_{3} } & {{\varvec{E}}_{3} } & {{\varvec{0}}_{3} } \\ {{\varvec{E}}_{3} } & {{\varvec{0}}_{3 \times 6} } & {} \\ {{\varvec{E}}_{6 \times 3} } & {{\varvec{E}}_{6} } & {} \\ \end{array} } \right]{\varvec{u}}_{S,id}$.
Prismatic joint	${\varvec{u}}_{P,id} = \left[ {\Delta_{iy} \;{\varvec{u}}_{j} } \right]$, ${\varvec{u}}_{J} = \left[ {\begin{array}{*{20}c} {\frac{{R_{P} (1,2)}}{{R_{P} (2,2)}}} & {{\varvec{a}}_{{{\text{P}}ix}} - \frac{{R_{P} (1,2){\varvec{a}}_{iy} }}{{R_{P} (2,2)}}} & {{\varvec{0}}_{1 \times 3} } \\ 1 & {{\varvec{0}}_{1 \times 6} } & {} \\ {\frac{{R_{P} (3,2)}}{{R_{P} (2,2)}}} & {{\varvec{a}}_{Piz} - \frac{{R_{P} (3,2){\varvec{a}}_{Piy} }}{{R_{P} (2,2)}}} & {{\varvec{0}}_{1 \times 3} } \\ {{\varvec{0}}_{3 \times 4} } & {{\varvec{E}}_{3} } & {} \\ {{\varvec{0}}_{6 \times 1} } & {{\varvec{E}}_{6} } & {} \\ \end{array} } \right]{\varvec{u}}_{P,id}$.	${\varvec{a}}_{{{\text{P}}ix}} = R_{P} (1,1){\varvec{Q}}_{P} (1,:) + R_{P} (1,3){\varvec{Q}}_{P} (2,:)$, ${\varvec{a}}_{{{\text{P}}iy}} = R_{P} (2,1){\varvec{Q}}_{P} (1,:) + R_{P} (2,3){\varvec{Q}}_{P} (2,:)$, ${\varvec{a}}_{{{\text{P}}iz}} = R_{P} (3,1){\varvec{Q}}_{P} (1,:) + R_{P} (3,3){\varvec{Q}}_{P} (2,:)$, ${\varvec{Q}}_{P} { = }\left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & 0 & 1 \\ \end{array} } \right]{\varvec{R}}_{P}^{ - 1}$.
Cylindrical joint	${\varvec{u}}_{C,id} = \left[ {\Delta_{iy} \;\varphi_{iy} \;{\varvec{u}}_{j} } \right]$, ${\varvec{u}}_{J} = \left[ {\begin{array}{*{20}c} {\frac{{R_{C} (1,2)}}{{R_{C} (2,2)}}} & 0 & {{\varvec{a}}_{{{\text{C}}ix}} - \frac{{R_{C} (1,2){\varvec{a}}_{Ciy} }}{{R_{C} (2,2)}}} & {{\varvec{0}}_{1 \times 3} } \\ 1 & {{\varvec{0}}_{1 \times 7} } & {} & {} \\ {\frac{{R_{C} (3,2)}}{{R_{C} (2,2)}}} & 0 & {{\varvec{a}}_{Ciz} - \frac{{R_{C} (3,2){\varvec{a}}_{Ciy} }}{{R_{C} (2,2)}}} & {{\varvec{0}}_{1 \times 3} } \\ 0 & {\frac{{R_{C} (1,2)}}{{R_{C} (2,2)}}} & {{\varvec{0}}_{1 \times 3} } & {{\varvec{a}}_{Cix} - \frac{{R_{C} (1,2){\varvec{a}}_{Ciy} }}{{R_{C} (2,2)}}} \\ 0 & 1 & {{\varvec{0}}_{1 \times 6} } & {} \\ 0 & {\frac{{R_{C} (3,2)}}{{R_{C} (2,2)}}} & {{\varvec{0}}_{1 \times 3} } & {{\varvec{a}}_{Ciz} - \frac{{R_{C} (3,2){\varvec{a}}_{Ciy} }}{{R_{C} (2,2)}}} \\ {{\varvec{0}}_{6 \times 2} } & {{\varvec{E}}_{6} } & {} & {} \\ \end{array} } \right]{\varvec{u}}_{C,id}$.	${\varvec{a}}_{{{\text{C}}ix}} = R_{P} (1,1){\varvec{Q}}_{{\text{C}}} (1,:) + R_{P} (1,3){\varvec{Q}}_{C} (2,:)$, ${\varvec{a}}_{{{\text{C}}iy}} = R_{P} (2,1){\varvec{Q}}_{{\text{C}}} (1,:) + R_{P} (2,3){\varvec{Q}}_{C} (2,:)$, ${\varvec{a}}_{Ciz} = R_{P} (3,1){\varvec{Q}}_{C} (1,:) + R_{{\text{C}}} (3,3){\varvec{Q}}_{{\text{C}}} (2,:)$, ${\varvec{Q}}_{{\text{C}}} \, = \,\left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & 0 & 1 \\ \end{array} } \right]{\varvec{R}}_{C}^{ - 1}$.
Screw joint	${\varvec{u}}_{W,id} = \left[ {\varphi_{iy} \;{\varvec{u}}_{j} } \right]$, ${\varvec{u}}_{J} = \left[ {\begin{array}{*{20}c} {{\varvec{N}}_{W\Delta i} } & {} & {} \\ {{\varvec{N}}_{W\varphi i} } & {{\varvec{0}}_{3} } & {{\varvec{N}}_{W\varphi j} } \\ {{\varvec{0}}_{6 \times 1} } & {{\varvec{E}}_{6} } & {} \\ \end{array} } \right]{\varvec{u}}_{W,id}$.	${\varvec{N}}_{W\varphi i} = \left[ {\begin{array}{*{20}c} {\frac{{R_{W} (1,2)}}{{R_{W} (2,2)}}} & 1 & {\frac{{R_{W} (3,2)}}{{R_{W} (2,2)}}} \\ \end{array} } \right]^{{\text{T}}}$, ${\varvec{N}}_{W\varphi j} = \left[ {\begin{array}{*{20}c} {{\varvec{a}}_{Wix} - \frac{{R_{W} (1,2){\varvec{a}}_{iy} }}{{R_{W} (2,2)}}} & {{\varvec{0}}_{1 \times 3} } & {{\varvec{a}}_{Wiz} - \frac{{R_{W} (3,2){\varvec{a}}_{Wiy} }}{{R_{W} (2,2)}}} \\ \end{array} } \right]^{{\text{T}}}$${\varvec{a}}_{{{\text{W}}ix}} = {\varvec{a}}_{{{\text{R}}ix}}$,${\varvec{a}}_{{{\text{W}}iy}} = {\varvec{a}}_{{{\text{R}}iy}}$,${\varvec{a}}_{{{\text{W}}iz}} = {\varvec{a}}_{{{\text{R}}iz}}$.
	${\varvec{N}}_{\Delta i} = \left[ {\begin{array}{*{20}c} {pR_{W} (1,2){\varvec{Q}}_{W2} {\varvec{N}}_{\varphi i} } & {R_{W} (1,1){\varvec{Q}}_{W1} (1,:) + R_{W} (1,2){\varvec{Q}}_{W2} + R_{W} (1,3){\varvec{Q}}_{W1} (2,:)} & {pR_{W} (1,2){\varvec{Q}}_{W2} ({\varvec{N}}_{\varphi j} - E_{3} )} \\ {pR_{W} (2,2){\varvec{Q}}_{W2} {\varvec{N}}_{\varphi i} } & {R_{W} (2,1){\varvec{Q}}_{W1} (1,:) + R_{W} (2,2){\varvec{Q}}_{W2} + R_{W} (2,3){\varvec{Q}}_{W1} (2,:)} & {pR_{W} (2,2){\varvec{Q}}_{W2} ({\varvec{N}}_{\varphi j} - E_{3} )} \\ {pR_{W} (3,2){\varvec{Q}}_{W2} {\varvec{N}}_{\varphi i} } & {R_{W} (3,1){\varvec{Q}}_{W1} (1,:) + R_{W} (3,2){\varvec{Q}}_{W2} + R_{W} (3,3){\varvec{Q}}_{W1} (2,:)} & {pR_{W} (3,2){\varvec{Q}}_{W2} ({\varvec{N}}_{\varphi j} - E_{3} )} \\ \end{array} } \right]$, ${\varvec{Q}}_{W1} = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & 0 & 1 \\ \end{array} } \right]{\varvec{R}}_{W}^{ - 1}$, ${\varvec{Q}}_{W2} = \left[ {\begin{array}{*{20}c} 0 & 1 & 0 \\ \end{array} } \right]{\varvec{R}}_{W}^{ - 1}$.
Rigid constraint	${\varvec{u}}_{g,id} = {\varvec{u}}_{j}$, ${\varvec{u}}_{J} = \left[ {\begin{array}{*{20}c} {{\varvec{E}}_{3} } & {[{\varvec{L}}_{ij} \times ]} \\ {{\varvec{0}}_{3} } & {{\varvec{E}}_{3} } \\ {{\varvec{E}}_{6} } & {} \\ \end{array} } \right]{\varvec{u}}_{g,id}$.