Dynamical analysis in exponential RED algorithm with communication delay

Abstract

In this paper, an exponential RED algorithm with communication delay is considered. By choosing the delay as a bifurcation parameter, we demonstrate that a Hopf bifurcation would occur when the delay exceeds a critical value. Some explicit formulas are worked out for determining the stability and the direction of the bifurcated periodic solutions by using the normal form theory and center manifold theory. Finally, numerical simulations supporting the theoretical analysis are provided.

1 Introduction

It is well known that Internet applications, such as the world wide web, file transfer, Usenet news and remote login, are delivered via the Transmission Control Protocol (TCP). With a spectacular growth of Internet applications, congestion control has become a subject of intense research activity. An uncontrolled network may suffer from severe congestion, which can cause high packet loss rates and increasing delays, the upper formation application systems performance drop, and it can even break the whole system by causing congestion collapse (or Internet meltdown) [1]. Thus congestion control is one of the critical issues for the efficient operation of the Internet. Many researchers have investigated the congestion control problems of the Internet and a lot of excellent and interesting results have been obtained, for example, Raina and Heckmann [2] investigated the stability properties of the congestion avoidance phase of TCP with drop tail. Guo et al. [3] investigated the stability of an exponential RED model with heterogeneous delays. Liu et al. [1] studied the bifurcation and chaotic behavior of the Transmission Control Protocol (TCP) and User Datagram Protocol (UDP) network with Random Early Detection (RED) queue management. Xu et al. [4] studied the Local Hopf bifurcation and global existence of periodic solutions of the following TCP system:

$$ \frac{dx(t)}{dt}=x(t-\tau) \biggl[\frac{M(1-p(x(t-\tau)))}{Nx(t)} - \frac{x(t)p(x(t-\tau))}{2M} \biggr], $$

(1.1)

where M, N are two positive constants, $p(y)$ is an increasing non-negative continuous function in $(0,+\infty)$ and τ is the round-trip propagation delay for each of the TCP connections. Guo et al. [5] considered the stability and Hopf bifurcation of the following congestion control model with two communication delays:

$$ \left \{ \textstyle\begin{array}{l} \dot{x}_{1}(t)=k_{1}x_{1}(t-\tau_{1}) [\frac{\alpha}{x_{1}(t)}-{\beta }x_{1}(t)p(t-\tau_{1}) ], \\ \dot{x}_{2}(t)=k_{2}x_{2}(t-\tau_{2}) [\frac{\alpha}{x_{2}(t)}-{\beta }x_{2}(t)p(t-\tau_{2}) ], \\ \dot{p}(t)={\gamma}p(t)[x_{1}(t-\tau_{1})+x_{2}(t-\tau_{2})-c], \end{array}\displaystyle \right .$$

(1.2)

where $x_{i}(t)$ is the rate at which source i transmits data at time t, α and β are positive real numbers, $p(t)$ is the loss probability function, $\tau_{i}$ is the round-trip delay for source i, c is the link capacity, k and γ are positive gain parameter, $i=1,2$. For more related work on congestion control, see [6–12].

Based on [7–9], Guo et al. [13] recently studied the following exponential RED algorithm coupled with TCP-Reno with a single source and with two sources:

$$ \left \{ \textstyle\begin{array}{l} \dot{x}_{1}(t)=k_{1}x_{1}(t-\tau) [\frac{1-p(t)}{\alpha^{2}x_{1}(t)}-\beta _{1}x_{1}(t)p(t) ], \\ \dot{x}_{2}(t)=k_{2}x_{2}(t-\tau) [\frac{1-p(t)}{\alpha^{2}x_{2}(t)}-\beta _{2}x_{2}(t)p(t) ], \\ \dot{p}(t)=k_{3}p(t)[x_{1}(t-\tau)+x_{2}(t-\tau)-c], \end{array}\displaystyle \right .$$

(1.3)

where $\dot{x}_{i}(t)=\frac{dx}{dt}$ ($i=1,2,3$) represent the transmission rate of the i source per second at time t, τ, $k_{i}$ ($i=1,2,3$) and $\beta_{j}$ ($j=1,2$) are the round-trip time (RTT), the positive gain parameter, and the decrease factor of the source i, respectively. By choosing the delay as a bifurcation parameter, Guo et al. [13] obtained the necessary and sufficient conditions for the existence of Hopf bifurcation and a formula for determining the direction of the Hopf bifurcation and the stability of bifurcating periodic solutions.

Motivated by [13] and considering that, when the number of sources is large, the simplified model can reflect the really exponential RED algorithm more closely, in this paper, we consider an exponential RED algorithm coupled with TCP-Reno with a single source and with three sources, then we have the following system:

$$ \left \{ \textstyle\begin{array}{l} \dot{x}_{1}(t)=k_{1}x_{1}(t-\tau) [\frac{1-p(t)}{\alpha^{2}x_{1}(t)}-\beta _{1}x_{1}(t)p(t) ], \\ \dot{x}_{2}(t)=k_{2}x_{2}(t-\tau) [\frac{1-p(t)}{\alpha^{2}x_{2}(t)}-\beta _{2}x_{2}(t)p(t) ], \\ \dot{x}_{3}(t)=k_{3}x_{3}(t-\tau) [\frac{1-p(t)}{\alpha^{2}x_{3}(t)}-\beta _{3}x_{3}(t)p(t) ], \\ \dot{p}(t)=k_{4}p(t)[x_{1}(t-\tau)+x_{2}(t-\tau)+x_{3}(t-\tau)-c]. \end{array}\displaystyle \right .$$

(1.4)

The purpose of this paper is to discuss the stability and the properties of the Hopf bifurcation of model (1.4). This paper is organized as follows. In Section 2, the stability of the equilibrium and the existence of a Hopf bifurcation at the equilibrium are studied. In Section 3, the direction of the Hopf bifurcation and the stability and periodic of bifurcating periodic solutions on the center manifold are determined. In Section 4, numerical simulations are carried out to illustrate the validity of the main results. Some main conclusions are drawn in Section 5.

2 Stability of the equilibrium and local Hopf bifurcations

Let $E_{*}(x_{1}^{*},x_{2}^{*},x_{3}^{*},p^{*})$ be the non-zero equilibrium point of system (1.4), then we have

$$ x_{1}^{*}=\frac{1}{\alpha}\sqrt{\frac{1-p^{*}}{\beta_{1}p^{*}}},\qquad x_{2}^{*}=\frac{1}{\alpha}\sqrt{\frac{1-p^{*}}{\beta_{2}p^{*}}},\qquad x_{3}^{*}=\frac{1}{\alpha}\sqrt{\frac{1-p^{*}}{\beta_{3}p^{*}}}, $$

(2.1)

where $p^{*}$ satisfies the following equation:

$$\sqrt{\frac{1-p^{*}}{\beta_{1}p^{*}}}+\sqrt{\frac{1-p^{*}}{\beta_{2}p^{*}}} +\sqrt{\frac{1-p^{*}}{\beta_{3}p^{*}}}=c \alpha. $$

Let

$$ \begin{aligned} &y_{1}(t)=x_{1}(t)-x_{1}^{*},\qquad y_{2}(t)=x_{2}(t)-x_{2}^{*}, \\ &y_{3}(t)=x_{3}(t)-x_{3}^{*},\qquad y_{4}(t)=p(t)-p^{*}. \end{aligned}$$

(2.2)

Substituting (2.2) into (1.4), we obtain the following linearized system:

$$ \left \{ \textstyle\begin{array}{l} \dot{y}_{1}(t)=a_{1}y_{1}(t)+a_{2}y_{4}(t), \\ \dot{y}_{2}(t)=b_{1}y_{2}(t)+b_{2}y_{4}(t), \\ \dot{y}_{3}(t)=c_{1}y_{3}(t)+c_{2}y_{4}(t), \\ \dot{y}_{4}(t)=d_{1}y_{1}(t-\tau)+d_{1}y_{2}(t-\tau)+d_{1}y_{3}(t-\tau), \end{array}\displaystyle \right .$$

(2.3)

where

$$\begin{aligned}& a_{1}=-2k_{1}\beta_{1}p^{*}x_{1}^{*}, \qquad b_{1}=-2k_{2}\beta_{2}p^{*}x_{2}^{*}, \qquad c_{1}=-2k_{3}\beta_{3}p^{*}x_{3}^{*},\qquad d_{1}=k_{3}p^{*}, \\& a_{2}=-\frac{k_{1}\beta_{1}(x_{1}^{*})^{2}}{1-p^{*}},\qquad b_{2}=-\frac{k_{2}\beta_{2}(x_{2}^{*})^{2}}{1-p^{*}}, \qquad c_{2}=-\frac{k_{3}\beta_{3}(x_{3}^{*})^{2}}{1-p^{*}}. \end{aligned}$$

Then the associated characteristic equation of (2.3) is

$$ \det \left ( \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{}} \lambda-a_{1} & 0 & 0 & -a_{2} \\ 0 & \lambda-b_{1} & 0 & -b_{2} \\ 0 & 0 & \lambda-c_{1} & -c_{2} \\ -d_{1}e^{-\lambda\tau} & -d_{1}e^{-\lambda\tau} & -d_{1}e^{-\lambda\tau} & \lambda \end{array}\displaystyle \right )=0.$$

(2.4)

Then we obtain the following fourth degree exponential polynomial equation:

$$ \lambda^{4}+m_{1}\lambda^{3}+m_{2} \lambda^{2}+m_{3}\lambda+\bigl(n_{1} \lambda^{2}+n_{2}\lambda +n_{3}\bigr)e^{-\lambda\tau}=0, $$

(2.5)

where

$$\begin{aligned}& m_{1}=-(a_{1}+b_{1}+c_{1}),\qquad m_{2}=a_{1}b_{1}+a_{1}c_{1}+b_{1}c_{1}, \qquad m_{3}=-a_{1}b_{1}c_{1}, \\& n_{1}=-(b_{2}d_{2}+c_{2}d_{3}+a_{2}d_{1}), \qquad n_{2}=b_{2}d_{2}(a_{1}+c_{1})+c_{2}d_{3}(a_{1}+b_{1})+a_{2}d_{1}(b_{1}+c_{1}), \\& n_{3}=-(a_{1}b_{2}c_{1}d_{2}+a_{1}b_{1}c_{2}d_{3}+a_{2}b_{1}c_{1}d_{1}). \end{aligned}$$

Let $\lambda=i\omega_{0}$, $\tau=\tau_{0}$, and substitute this into (2.5), for the sake of simplicity, denote $\omega_{0}$ and $\tau_{0}$ by ω, τ, respectively, Separating the real and imaginary parts, we have

$$\begin{aligned}& \bigl(n_{3}-n_{1}\omega^{2}\bigr)\cos\omega \tau+n_{2}\omega\sin\omega\tau =m_{2}\omega^{2}- \omega^{4}, \end{aligned}$$

(2.6)

$$\begin{aligned}& n_{2}\omega\cos\omega\tau-\bigl(n_{3}-n_{1} \omega^{2}\bigr)\sin\omega\tau=m_{1}\omega ^{3}-m_{3}\omega. \end{aligned}$$

(2.7)

Taking the square on both sides of (2.6) and (2.7) and summing them up, we obtain

$$\bigl(n_{3}-n_{1}\omega^{2}\bigr)^{2}+(n_{2} \omega)^{2}=\bigl(m_{2}\omega^{2}- \omega^{4}\bigr)^{2}+\bigl(m_{1}\omega ^{3}-m_{3}\omega\bigr)^{2}, $$

i.e.,

$$ \omega^{8}+(m_{1}-2n_{2}) \omega^{6}+\bigl(n_{2}-2m_{1}m_{3}-n_{1}^{2} \bigr)\omega ^{4}+\bigl(m_{3}+2n_{1}n_{3}-n_{2}^{2} \bigr)\omega^{2}-n_{3}^{2}=0. $$

(2.8)

Let $p=m_{1}-2n_{2}$, $q=n_{2}-2m_{1}m_{3}-n_{1}^{2}$, $u=m_{3}+2n_{1}n_{3}-n_{2}^{2}$, $v=-n_{3}^{2}$, $z=\omega^{2}$. Then equation (2.8) becomes

$$ z^{4}+pz^{3}+qz^{2}+uz+v=0. $$

(2.9)

Let

$$ l(z)=z^{4}+pz^{3}+qz^{2}+uz+v. $$

(2.10)

If the coefficients $k_{i}$ ($i=1,2,3,4$), α, $\beta_{j}$ ($j=1,2,3$) of system (1.4) are given, it is easy to use computer to calculate the roots of (2.9). Since $\lim_{z\rightarrow\infty}l(z)=+\infty$ and $v<0$, we can conclude that (2.9) has at least one positive real root.

Without loss of generality, we assume that (2.9) has four positive roots, denoted by $z_{1}$, $z_{2}$, $z_{3}$, $z_{4}$, respectively. Then (2.8) has four positive roots

$$\omega_{1}=\sqrt{z_{1}},\qquad \omega_{2}= \sqrt{z_{2}},\qquad \omega_{3}=\sqrt{z_{3}},\qquad \omega _{4}=\sqrt{z_{4}}. $$

By (2.6) and (2.7) we have

$$ \tau_{k}^{(j)}=\frac{1}{\omega_{k}} \biggl[ \arccos\frac{(m_{2}\omega _{k}^{2}-m^{4})(n_{3}-n_{1}\omega_{k}^{2})+ (m_{1}\omega_{k}^{3}-m_{3}\omega)n_{2}\omega}{(n_{3}-n_{1}\omega_{k}^{2})^{2}+(n_{2}\omega )^{2}}+2j\pi \biggr], $$

(2.11)

where $k=1, 2, 3, 4$ and $j=0, 1, 2, \ldots$ . Then $\pm{i\omega_{k}}$ are a pair of purely imaginary roots of equation (2.5) with $\tau=\tau_{k}^{(j)}$. Obviously, the sequence $\{\tau_{k}^{(j)}\}_{j=0}^{+\infty}$ is increasing, and

$$\lim_{j\rightarrow{+\infty}}\tau_{k}^{(j)}=+\infty,\quad k=1, 2, 3, 4. $$

Then we can define

$$ \tau_{0}=\tau_{k0}^{(0)}=\min _{1\leq{k}\leq4}\bigl\{ \tau_{k}^{(0)}\bigr\} ,\qquad \omega_{0}=\omega_{k0}. $$

(2.12)

Note that, when $\tau=0$, (2.5) becomes

$$ \lambda^{4}+q_{1}\lambda^{3}+q_{2} \lambda^{2}+q_{3}\lambda+q_{4}=0, $$

(2.13)

where

$$\begin{aligned}& q_{1}=-(a_{1}+b_{1}+c_{1}), \\& q_{2}=(a_{1}b_{1}+a_{1}c_{1}+b_{1}c_{1})-(b_{2}d_{2}+c_{2}d_{3}+a_{2}d_{1}), \\& q_{3}=b_{2}d_{2}(a_{1}+c_{1})+c_{2}d_{3}(a_{1}+b_{1})+a_{2}d_{1}(c_{1}+d_{1})-a_{1}b_{1}c_{1}, \\& q_{4}=a_{1}b_{2}c_{1}d_{2}+a_{1}b_{1}c_{2}d_{3}+a_{2}b_{1}c_{1}d_{1}. \end{aligned}$$

A set of necessary and sufficient conditions for all roots of (2.13) to have a negative real part is given by the well-known Routh-Hurwitz criteria in the following form:

$$ q_{1}>0,\qquad q_{1}q_{2}-q_{3}>0, \qquad q_{1}q_{2}q_{3}-q_{3}^{2}-q_{1}^{2}q_{4}>0, \qquad q_{4}>0. $$

(2.14)

Let $\lambda(\tau)=\alpha(\tau)+i\omega(\tau)$ be the root of equation (2.5) near $\tau=\tau_{k}^{(j)}$ satisfying $\alpha(\tau_{k}^{(j)})=0$, $\omega(\tau_{k}^{(j)})=\omega_{k}$. Then the following lemma holds.

Lemma 2.1

Suppose that $l'(z_{k})\neq0$, where $l(z)$ is defined by (2.10). If $\tau=\tau_{k}^{(j)}$, then $\pm{i\omega_{k}}$ are a pair of simple purely imaginary roots of equation (2.5). Moreover,

$$\biggl[\frac{d({\textrm{R}e}\lambda(\tau))}{d\tau} \biggr]_{\tau=\tau _{k}^{(j)}}\neq0 $$

and the sign of $[\frac{d({\textrm{R}e}\lambda(\tau))}{d\tau} ]_{\tau=\tau_{k}^{(j)}}$ is consistent with that of $l'(z_{k})$.

Proof

Let

$$ F(\lambda)=\lambda^{4}+m_{1} \lambda^{3}+m_{2}\lambda^{2}+m_{3}\lambda, \qquad H(\lambda)=n_{1}\lambda^{2}+n_{2} \lambda+n_{3}. $$

(2.15)

Then (2.5) can be written as

$$ F(\lambda)+H(\lambda)e^{-\lambda\tau}=0, $$

(2.16)

which leads to

$$ F(\lambda)\overline{F(\lambda)}-H(\lambda)\overline{H(\lambda)}=0. $$

(2.17)

Thus, together with (2.9) and (2.10), we get

$$ l\bigl(\omega^{2}\bigr)=F(i\omega)\overline{F(i \omega)}-H(i\omega)\overline {H(i\omega)}. $$

(2.18)

Differentiating both sides of equation (2.5) with respect to ω, we obtain

$$ 2{\omega}l'\bigl(\omega^{2}\bigr)=i \bigl[F'(i\omega)\overline{F(i\omega)}-\overline {F'(i \omega)}F(i\omega) -H'(i\omega)\overline{H(i\omega)}+ \overline{H'(i\omega)}H(i\omega)\bigr]. $$

(2.19)

If $i\omega_{k}$ is not simple, then $\omega_{k}$ must satisfy

$${\biggr.\frac{d}{d\lambda} \bigl[F(\lambda)+H(\lambda)e^{-\lambda\tau _{k}^{(j)}} \bigr] \biggl|_{\lambda=i\omega_{k}}}=0, $$

i.e.,

$$F'(i\omega_{k})+H'(i\omega_{k})e^{-\omega_{k}\tau_{k}^{(j)}}- \tau _{k}^{(j)}H(i\omega_{k})e^{-\omega_{k}\tau_{k}^{(j)}}=0. $$

By (2.16), we obtain

$$\tau_{k}^{(j)}=\frac{H'(i\omega_{k})}{H(i\omega_{k})}-\frac{F'(i\omega _{k})}{F(i\omega_{k})}. $$

Thus, by (2.17) and (2.19), we obtain

$$\begin{aligned} \operatorname{Im}\tau_{k}^{(j)} =&\operatorname{Im} \biggl\{ \frac {H'(i\omega_{k})}{H(i\omega_{k})}-\frac{F'(i\omega_{k})}{F(i\omega _{k})} \biggr\} =\operatorname{Im} \biggl\{ \frac{H'(i\omega_{k})\overline{H(i\omega_{k})}}{H(i\omega _{k})\overline{H(i\omega_{k})}} -\frac{F'(i\omega_{k})\overline{F(i\omega_{k})}}{F(i\omega_{k})\overline {F(i\omega_{k})}} \biggr\} \\ =&\operatorname{Im} \biggl\{ \frac{H'(i\omega_{k})\overline{H(i\omega _{k})}-F'(i\omega_{k})\overline{F(i\omega_{k})}}{ F(i\omega_{k})\overline{F(i\omega_{k})}} \biggr\} =\frac{\omega_{k}l'(\omega _{k}^{2})}{|F(i\omega_{k})|^{2}}. \end{aligned}$$

Since $\tau_{k}^{(j)}$ is real, we have $l'(z_{k})=l'(\omega_{k}^{2})=0$, which is a contradiction to the condition $l'(z_{k})\neq0$. This proves the first part of Lemma 2.1.

Taking the derivative of λ with respect to τ in (2.5), it is easy to obtain

$$\bigl[F'(\lambda)+H'(\lambda)e^{-\lambda\tau}-{ \tau}H(\lambda )e^{-\lambda\tau}\bigr] \frac{d\lambda}{d\tau}-{\lambda}H( \lambda)e^{-\lambda\tau}=0, $$

which means

$$\begin{aligned} \frac{d\lambda(\tau)}{d\tau} =&\frac{{\lambda}H(\lambda )}{F'(\lambda)e^{\lambda\tau} +H'(\lambda)-{\tau}H(\lambda)} \\ =&\frac{{\lambda}H(\lambda)[\overline{F'(\lambda)}e^{\lambda\tau }+\overline{H'(\lambda)} -{\tau}\overline{H(\lambda)}]}{|F'(\lambda)e^{\lambda\tau }+H'(\lambda)-{\tau}H(\lambda)|^{2}} \\ =&\frac{\lambda[-\overline{F'(\lambda)}F(\lambda)+\overline {H'(\lambda)}H(\lambda) -{\tau}|H(\lambda)|^{2}]}{|F'(\lambda)e^{\lambda\tau}+H'(\lambda )-{\tau}H(\lambda)|^{2}}. \end{aligned}$$

It follows from this together with (2.19) that

$$\begin{aligned}& {\biggl.\frac{d(\operatorname{Re}\lambda(\tau))}{d\tau} \biggr|_{\tau=\tau_{k}^{(j)}}} \\& \quad = {\biggl.\frac{\operatorname{Re}\{\lambda[-\overline{F'(\lambda)}F(\lambda)+\overline {H'(\lambda)}H(\lambda) -{\tau}|H(\lambda)|^{2}]\}}{|F'(\lambda)e^{\lambda\tau}+H'(\lambda )-{\tau}H(\lambda)|^{2}} \biggr|_{\tau=\tau_{k}^{(j)}}} \\& \quad = \frac{i\omega_{k}[-\overline{F'(i\omega_{k})}F(i\omega_{k})+\overline {H'(i\omega_{k})}H(i\omega_{k}) +F'(i\omega_{k})\overline{F(i\omega_{k})}-H'(i\omega_{k})\overline {H(i\omega_{k})}]}{ 2|F'(i\omega_{k})e^{i\tau_{k}^{(j)}\omega_{k}}+H'(i\omega_{k})-\tau _{k}^{(j)}H(i\omega_{k})|^{2}} \\& \quad = \frac{\omega_{k}^{2}l'(\omega_{k}^{2})}{ |F'(i\omega_{k})e^{i\tau_{k}^{(j)}\omega_{k}}+H'(i\omega_{k})-\tau _{k}^{(j)}H(i\omega_{k})|^{2}} \\& \quad = \frac{\omega_{k}^{2}l'(z_{k})}{ |F'(i\omega_{k})e^{i\tau_{k}^{(j)}\omega_{k}}+H'(i\omega_{k})-\tau _{k}^{(j)}H(i\omega_{k})|^{2}}\neq0. \end{aligned}$$

Obviously, the sign of $\frac{d(\operatorname{Re}\lambda(\tau))}{d\tau} {|}_{\tau=\tau_{k}^{(j)}}$ is determined by that of $l'(z_{k})$. This completes the proof. □

In order to investigate the distribution of roots of the transcendental equation (2.5), the following lemma, which is stated in [14], is useful.

Lemma 2.2

[14]

For the transcendental equation

$$\begin{aligned} P\bigl(\lambda,e^{-\lambda\tau_{1}},\ldots,e^{-\lambda\tau_{m}}\bigr) =& \lambda^{n}+p_{1}^{(0)}\lambda^{n-1}+ \cdots+p_{n-1}^{(0)}\lambda+p_{n}^{(0)} \\ &{}+ \bigl[p_{1}^{(1)}\lambda^{n-1}+ \cdots+p_{n-1}^{(1)}\lambda +p_{n}^{(1)} \bigr]e^{-\lambda\tau_{1}}+\cdots \\ &{}+ \bigl[p_{1}^{(m)}\lambda^{n-1}+ \cdots+p_{n-1}^{(m)}\lambda +p_{n}^{(m)} \bigr]e^{-\lambda\tau_{m}}=0, \end{aligned}$$

as $(\tau_{1},\tau_{2},\tau_{3},\ldots,\tau_{m})$ vary, the sum of orders of the zeros of $P(\lambda, e^{-\lambda\tau_{1}},\ldots,e^{-\lambda\tau_{m}})$ in the open right half plane can change, and only a zero appears on or crosses the imaginary axis.

From Lemma 2.2, it is easy to obtain the following results.

Theorem 2.3

Let $\tau_{k}^{(j)}$ and $\tau_{0}$ be defined by (2.11) and (2.12), respectively.

• (i) If (2.14) holds, the equilibrium $E_{*}(x_{1}^{*}, x_{2}^{*}, x_{3}^{*}, p^{*})$ of system (1.4) is asymptotically stable for $\tau\in[0, \tau_{0})$.

• (ii) If (2.14) and $l'(z_{k})$ hold, then system (1.4) undergoes a Hopf bifurcation at the equilibrium $E_{*}(x_{1}^{*}, x_{2}^{*}, x_{3}^{*}, p^{*})$ when $\tau=\tau_{k}^{(j)}$, i.e., system (1.4) has a branch of periodic solutions bifurcating from the equilibrium $E_{*}(x_{1}^{*}, x_{2}^{*}, x_{3}^{*}, p^{*})$ near $\tau=\tau_{k}^{(j)}$.

3 Direction and stability of the Hopf bifurcation

In the previous section, we have obtained conditions for Hopf bifurcation to occur when $\tau=\tau_{k}^{(j)}$. In this section, we shall derive the explicit formulas for determining the direction, stability, and period of these periodic solutions bifurcating from the equilibrium $E_{*}(x_{1}^{*}, x_{2}^{*}, x_{3}^{*}, p^{*})$ at these critical value of τ, by using techniques from the normal form and center manifold theory [15], Throughout this section, we always assume that system (2.2) undergoes Hopf bifurcation at the equilibrium $E_{*}(x_{1}^{*}, x_{2}^{*}, x_{3}^{*}, p^{*})$ for $\tau=\tau_{k}^{(j)}$, and then $\pm{i\omega_{k}}$ are corresponding purely imaginary roots of the characteristic equation at the equilibrium $E_{*}(x_{1}^{*}, x_{2}^{*}, x_{3}^{*}, p^{*})$. The linear part of system (1.4) at $E_{*}(x_{1}^{*}, x_{2}^{*}, x_{3}^{*}, p^{*})$ is given by

$$ \left \{ \textstyle\begin{array}{l} \dot{y}_{1}(t)=a_{1}y_{1}(t)+a_{2}y_{4}(t), \\ \dot{y}_{2}(t)=b_{1}y_{2}(t)+b_{2}y_{4}(t), \\ \dot{y}_{3}(t)=c_{1}y_{3}(t)+c_{2}y_{4}(t), \\ \dot{y}_{4}(t)=d_{1}y_{1}(t-\tau)+d_{1}y_{2}(t-\tau)+d_{1}y_{3}(t-\tau), \end{array}\displaystyle \right .$$

(3.1)

and the non-linear part is given by

$$ f(\mu, u_{t})=(f_{1}, f_{2}, f_{3}, f_{4})^{T}, $$

(3.2)

where

$$\begin{aligned}& f_{1} = a_{3}y_{1}^{2}(t)+a_{4}y_{1}(t)y_{1}(t- \tau)+a_{5}y_{1}(t)y_{4}(t)+a_{6}y_{1}(t- \tau )y_{4}(t) \\& \hphantom{f_{1} ={}}{}+a_{7}y_{1}^{3}(t)+a_{8}y_{1}^{2}(t)y_{1}(t- \tau )+a_{9}y_{1}^{2}(t)y_{4}(t)+a_{10}y_{1}(t)y_{1}(t- \tau)y_{4}(t)+\mathrm{h.o.t.}, \\& f_{2} = b_{3}y_{2}^{2}(t)+b_{4}y_{2}(t)y_{2}(t- \tau)+b_{5}y_{2}(t)y_{4}(t)+b_{6}y_{2}(t- \tau )y_{4}(t) \\& \hphantom{f_{2} ={}}{}+b_{7}y_{2}^{3}(t)+b_{8}y_{2}^{2}(t)y_{2}(t- \tau )+b_{9}y_{2}^{2}(t)y_{4}(t)+b_{10}y_{2}(t)y_{2}(t- \tau)y_{4}(t)+\mathrm{h.o.t.}, \\& f_{3} = c_{3}y_{3}^{2}(t)+c_{4}y_{3}(t)y_{3}(t- \tau)+c_{5}y_{3}(t)y_{4}(t)+c_{6}y_{3}(t- \tau )y_{4}(t) \\& \hphantom{f_{3} ={}}{}+c_{7}y_{3}^{3}(t)+c_{8}y_{3}^{2}(t)y_{3}(t- \tau )+c_{9}y_{3}^{2}(t)y_{4}(t)+c_{10}y_{3}(t)y_{3}(t- \tau)y_{4}(t)+\mathrm{h.o.t.}, \\& f_{4} = d_{1}y_{1}(t-\tau)y_{4}(t)+d_{1}y_{2}(t- \tau)y_{4}(t)+d_{1}y_{3}(t-\tau )y_{4}(t), \end{aligned}$$

where

$$\begin{aligned}& a_{3}=k_{1}\beta_{1}p^{*}x_{1}^{*},\qquad a_{4}=-2k_{1}\beta_{1}p^{*},\qquad a_{5}=\frac{k_{1}\beta_{1}x_{1}^{*}(2p^{*}-1)}{1-p^{*}},\qquad a_{6}=\frac{k_{1}\beta_{1}x_{1}^{*}}{1-p^{*}}, \\& a_{7}=-\frac{k_{1}\beta_{1}p^{*}}{x_{1}^{*}}, \qquad a_{8}=\frac{k_{1}\beta_{1}p^{*}}{x_{1}^{*}}, \qquad a_{9}=-\frac{k_{1}\beta_{1}p^{*}}{1-p^{*}},\qquad a_{10}= \frac{k_{1}\beta_{1}(2p^{*}-1)}{1-p^{*}}, \\& b_{3}=k_{2}\beta_{2}p^{*}x_{2}^{*},\qquad b_{4}=-2k_{2}\beta_{2}p^{*},\qquad b_{5}= \frac{k_{2}\beta_{2}x_{2}^{*}(2p^{*}-1)}{1-p^{*}}, \\& b_{6}=\frac{k_{2}\beta_{2}x_{2}^{*}}{1-p^{*}},\qquad b_{7}=-\frac{k_{2}\beta_{2}p^{*}}{x_{2}^{*}},\qquad b_{8}=\frac{k_{2}\beta_{2}p^{*}}{x_{2}^{*}}, \\& b_{9}=-\frac{k_{2}\beta_{2}p^{*}}{1-p^{*}},\qquad b_{10}= \frac{k_{2}\beta_{2}(2p^{*}-1)}{1-p^{*}} ,\qquad d_{1}=k_{4}. \end{aligned}$$

Set $\tau=\tau_{k}^{(j)}+\mu$ and denote

$$\begin{aligned} C^{k}[-\tau,0] =&\bigl\{ \varphi|\varphi:[-\tau,0]\rightarrow{R^{4}}, \mbox{each component of }\varphi \\ &\mbox{has }k\mbox{th order continuous derivative}\bigr\} . \end{aligned}$$

For convenience, denote $C[-\tau, 0]$ by $C^{0}[-\tau, 0]$.

For $\varphi(\theta)=(\varphi_{1}(\theta), \varphi_{2}(\theta), \varphi_{3}(\theta), \varphi_{4}(\theta))^{T}\in{C([-\tau, 0], R^{4})}$, define a family of operators

$$ L_{\mu}\varphi=B\varphi(0)+B_{1}\varphi(-\tau) $$

(3.3)

and

$$ G(\mu,\varphi)=(k_{1}, k_{2}, k_{3}, k_{4})^{T}, $$

(3.4)

where

$$\begin{aligned}& B=\left ( \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{}} a_{1} & 0 & 0 & a_{2} \\ 0 & b_{1} & 0 & b_{2} \\ 0 & 0 & c_{1} & c_{2} \\ 0 & 0 & 0 & 0 \end{array}\displaystyle \right ) , \qquad B_{1}= \left ( \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{}} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ d_{1} & d_{1} & d_{1} & 0 \end{array}\displaystyle \right ), \\& k_{1}=a_{3}\varphi_{1}^{2}(0)+a_{4} \varphi_{1}(0)\varphi_{1}(-\tau)+a_{5}\varphi _{1}(0)\varphi_{4}(0)+a_{6}\varphi_{1}(- \tau)\varphi_{4}(0) \\& \hphantom{k_{1}={}}{}+a_{7}\varphi_{1}^{3}(0)+a_{8} \varphi_{1}^{2}(0)\varphi_{1}(- \tau)+a_{9}\varphi _{1}^{2}(t) \varphi_{4}(0)+a_{10}\varphi_{1}(t) \varphi_{1}(-\tau)\varphi _{4}(0)+o\bigl(\|\varphi \|^{4}\bigr), \\& k_{2} = b_{3}\varphi_{2}^{2}(0)+b_{4} \varphi_{2}(0)\varphi_{2}(-\tau)+b_{5}\varphi _{2}(0)\varphi_{4}(0)+b_{6}\varphi_{2}(- \tau)y_{4}(0) \\& \hphantom{k_{2} ={}}{}+b_{7}\varphi_{2}^{3}(0)+b_{8} \varphi_{2}^{2}(0)\varphi_{2}(-\tau)+b_{9} \varphi _{2}^{2}(0)\varphi_{4}(0)+b_{10} \varphi_{2}(0)\varphi_{2}(-\tau)\varphi _{4}(0)+o \bigl(\|\varphi\|^{4}\bigr), \\& k_{3} = c_{3}\varphi_{3}^{2}(0)+c_{4} \varphi_{3}(0)\varphi_{3}(-\tau)+c_{5}\varphi _{3}(0)\varphi_{4}(0)+c_{6}\varphi_{3}(t- \tau)\varphi_{4}(0) \\& \hphantom{k_{3} ={}}{}+c_{7}\varphi_{3}^{3}(0)+c_{8} \varphi_{3}^{2}(0)\varphi_{3}\bigl(0-\tau _{k}^{(j)}\bigr)+c_{9}\varphi_{3}^{2}(0) \varphi_{4}(0)+c_{10}\varphi_{3}(0)\varphi _{3}(-\tau)\varphi_{4}(0)+o\bigl(\|\varphi\|^{4} \bigr), \\& k_{4} = d_{1}\varphi_{1}(-\tau) \varphi_{4}(0)+d_{1}\varphi_{2}(-\tau)\varphi _{4}(0)+d_{1}\varphi_{3}(-\tau) \varphi_{4}(0), \end{aligned}$$

and $L_{\mu}$ is a one-parameter family of bounded linear operators in $C([-\tau, 0], R^{4})\rightarrow{R^{4}}$. By the Riesz representation theorem, there exists a matrix whose components are bounded variation functions $\eta(\theta,\mu)$ in $[-\tau, 0]\rightarrow{R^{4^{2}}}$, such that

$$ L_{\mu}\varphi= \int_{-\tau}^{0}d\eta(\theta, \mu)\varphi(\theta). $$

(3.5)

In fact, choosing

$$ \eta(\theta,\mu)=B\delta(\theta)+B_{1}\delta(\theta+ \tau), $$

(3.6)

where $\delta(\theta)$ is the Dirac delta function, then (3.5) is satisfied. For $(\varphi_{1}, \varphi_{2}, \varphi_{3}, \varphi_{4})\in(C^{1}[-\tau, 0], R^{4})$, define

$$ A(\mu)\varphi=\left \{ \textstyle\begin{array}{l@{\quad}l} \frac{d\varphi(\theta)}{d\theta}, &-\tau\leq\theta< 0, \\ \int_{-\tau}^{0}d\eta(s, \mu)\varphi(s), &\theta=0 \end{array}\displaystyle \right . $$

(3.7)

and

$$ R\varphi=\left \{ \textstyle\begin{array}{l@{\quad}l} 0, &-\tau\leq\theta< 0, \\ f(\mu, \varphi), &\theta=0. \end{array}\displaystyle \right . $$

(3.8)

Then (1.4) is equivalent to the abstract differential equation

$$ \dot{u_{t}}=A(\mu)u_{t}+R( \mu)u_{t}, $$

(3.9)

where $u=(u_{1}, u_{2}, u_{3}, u_{4})^{T}$, $u_{t}(\theta)=u(t+\theta)$, $\theta\in[-\tau , 0]$.

For $\psi\in{C([-\tau, 0], (R^{4})^{*})}$, define

$$ A^{*}\psi(s)=\left \{ \textstyle\begin{array}{l@{\quad}l} -\frac{d\psi(s)}{ds}, &s\in{(0,\tau]}, \\ \int_{-\tau}^{0}d\eta^{T}(t,0)\psi(-t),&s=0. \end{array}\displaystyle \right . $$

(3.10)

For $\phi\in{C([-\tau, 0], R^{4})}$ and $\psi\in{C([0, \tau], (R^{4})^{*})}$, define the bilinear form

$$ \langle\psi,\phi\rangle=\bar{\psi}(0)\phi(0)- \int_{-\tau}^{0} \int _{\xi=0}^{\theta}\psi^{T}(\xi-\theta)\, d \eta(\theta)\phi(\xi)\, d\xi, $$

(3.11)

where $\eta(\theta)=\eta(\theta,0)$. We have the following result on the relation between the operators $A=A(0)$ and $A^{*}$.

Lemma 3.1

$A=A(0)$ and $A^{*}$ are adjoint operators.

Proof

Let $\phi\in{C^{1}([-\tau, 0], R^{4})}$ and $\psi\in{C^{1}([0, \tau], R^{4})^{*}}$. It follows from (3.11) and the definitions of $A=A(0)$ and $A^{*}$ that

$$\begin{aligned} \bigl\langle \psi(s), A(0)\phi(\theta)\bigr\rangle =&\bar{\psi}(0)A(0)\phi(0)- \int_{-\tau _{k}^{(j)}}^{0} \int_{\xi=0}^{\theta} \bar{\psi}(\xi-\theta)\,d\eta( \theta)A(0)\phi(\xi)\,d\xi \\ =&\bar{\psi}(0) \int_{-\tau_{k}^{(j)}}^{0}d\eta(\theta)\phi(\theta )- \int_{-\tau_{k}^{(j)}}^{0} \int_{\xi=0}^{\theta} \bar{\psi}(\xi-\theta)\,d\eta( \theta)A(0)\phi(\xi)\,d\xi \\ =&\bar{\psi}(0) \int_{-\tau_{k}^{(j)}}^{0}d\eta(\theta)\phi(\theta )- \int_{-\tau_{k}^{(j)}}^{0}\bigl[ \bar{\psi}(\xi-\theta)\,d\eta( \theta)\phi(\xi)\bigr]_{\xi=0}^{\theta} \\ &{}+ \int_{-\tau_{k}^{(j)}}^{0} \int_{\xi=0}^{\theta} \frac{d\bar{\psi}(\xi-\theta)}{d\xi}\,d\eta(\theta)\phi( \xi)\,d\xi \\ =& \int_{-\tau_{k}^{(j)}}^{0}\bar{\psi}(-\theta)\,d\eta(\theta) \phi(0)- \int_{-\tau_{k}^{(j)}}^{0} \int_{\xi=0}^{\theta} \biggl[-\frac{d\bar{\psi}(\xi-\theta)}{d\xi} \biggr]\,d \eta(\theta)\phi(\xi )\,d\xi \\ =&A*\bar{\psi}(0)\phi(0)- \int_{-\tau_{k}^{(j)}}^{0} \int_{\xi =0}^{\theta} A^{*}\bar{\psi}(\xi-\theta)\,d\eta( \theta)\phi(\xi)\,d\xi \\ =&\bigl\langle A^{*}\psi(s), \phi(\theta)\bigr\rangle . \end{aligned}$$

This shows that $A=A(0)$ and $A^{*}$ are adjoint operators and the proof is complete. □

By the discussions in Section 2, we know that $\pm{i\omega_{k}}$ are eigenvalues of $A(0)$, and they are also eigenvalues of $A^{*}$ corresponding to $i\omega_{k}$ and $-i\omega_{k}$, respectively. We have the following result.

Lemma 3.2

The vector

$$q(\theta)=(1, r_{1}, r_{2}, r_{3})^{T}e^{i\omega_{k}\theta}, \quad \theta\in[-\tau, 0], $$

is the eigenvector of $A(0)$ corresponding to the eigenvalue $i\omega_{k}$, and

$$q^{*}(s)=D\bigl(1, r_{1}^{*}, r_{2}^{*}, r_{3}^{*} \bigr)e^{i\omega_{k}{s}}, \quad s\in[0,\tau], $$

is the eigenvector of $A^{*}$ corresponding to the eigenvalue $-i\omega_{k}$, moreover, $\langle q^{*}(s), q(\theta)\rangle=1$, where

$$ D=\frac{1}{C}, $$

(3.12)

where

$$C=1+\sum_{i=1}^{3}\bar{r}_{i}r_{i}^{*}+(1+ \bar{r}_{1}+\bar{r}_{2}+\bar {r}_{3})d_{1}r_{3}^{*}e^{i\omega_{k}\tau_{k}^{(j)}}. $$

Proof

Let $q(\theta)$ be the eigenvector of $A(0)$ corresponding to the eigenvalue $i\omega_{k}$ and $q^{*}(s)$ be the eigenvector of $A^{*}$ corresponding to the eigenvalue $-i\omega_{k}$, namely, $A(0)q(\theta)=i\omega_{k}q(\theta)$ and $A^{*}q(s)=-i\omega_{k}q^{*}(s)$. From the definitions of $A(0)$ and $A^{*}$, we have $A(0)q(\theta)=dq(\theta)/d\theta$ and $A^{*}q(s)=-dq^{*}(s)/ds$. Thus, $q(\theta)=q(0)e^{i\omega_{k}\theta}$ and $q^{*}(s)=q(0)e^{i\omega_{0}s}$. In addition,

$$\begin{aligned} \int_{-\tau_{k}^{(j)}}^{0}d\eta(\theta)q(\theta) =&\left ( \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{}} a_{1} & 0 & 0 & a_{2} \\ 0 & b_{1} & 0 & b_{2} \\ 0 & 0 & c_{1} & c_{2} \\ 0 & 0 & 0 & 0 \end{array}\displaystyle \right )q(0)+\left ( \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{}} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ d_{1} & d_{1} & d_{1} & 0 \end{array}\displaystyle \right )q\bigl(-\tau_{k}^{(j)}\bigr) \\ =&A(0)q(0)=i\omega_{k}q(0). \end{aligned}$$

(3.13)

That is,

$$ \left ( \textstyle\begin{array}{@{}c@{}} a_{1}+a_{2}r_{3} \\ b_{1}r_{1}+b_{2}r_{3} \\ c_{1}r_{2}+c_{2}r_{3} \\ d_{1}(1+r_{1}+r_{2})e^{-i\omega_{k}\tau_{k}^{(j)}} \end{array}\displaystyle \right ) =\left ( \textstyle\begin{array}{@{}c@{}} i\omega_{k} \\ i\omega_{k}r_{1} \\ i\omega_{k}r_{2} \\ i\omega_{k}r_{3} \end{array}\displaystyle \right ). $$

(3.14)

Therefore, we can easily obtain

$$r_{1}=\frac{b_{2}(a_{1}-i\omega_{k})}{a_{2}(b_{1}-i\omega_{k})},\qquad r_{2}=\frac{c_{2}(a_{1}-i\omega_{k})}{a_{2}(c_{1}-i\omega_{k})}, \qquad r_{3}=\frac{i\omega_{k}-a_{1}}{a_{2}}. $$

On the other hand,

$$\begin{aligned} \int_{-\tau_{k}^{(j)}}^{0}q^{*}(-t)\,d\eta(t) =&\left ( \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{}} a_{1} & 0 & 0 & 0\\ 0 & b_{1} & 0 & 0 \\ 0 & 0 & c_{1} & 0 \\ a_{2} & b_{2} & c_{2} & 0 \end{array}\displaystyle \right )q(0)+\left ( \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{}} 0 & 0 & 0 & d_{1} \\ 0 & 0 & 0 & d_{1} \\ 0 & 0 & 0 & d_{1} \\ 0 & 0 & 0 & 0 \end{array}\displaystyle \right )q^{*}\bigl(-\tau_{k}^{(j)}\bigr) \\ =&A^{*}q^{*}(0)=-i\omega_{0}q^{*}(0). \end{aligned}$$

(3.15)

Namely,

$$ \left ( \textstyle\begin{array}{@{}c@{}} a_{1}+d_{1}r_{3}^{*}e^{-i\omega_{k}\tau_{k}^{(j)}} \\ b_{1}r_{1}^{*}+d_{1}r_{3}^{*}e^{-i\omega_{k}\tau_{k}^{(j)}} \\ c_{1}r_{2}^{*}+d_{1}r_{3}^{*}e^{-i\omega_{k}\tau_{k}^{(j)}} \\ a_{2}+b_{2}r_{1}^{*}+c_{2}r_{3}^{*} \end{array}\displaystyle \right ) =\left ( \textstyle\begin{array}{@{}c@{}} -i\omega_{k} \\ -i\omega_{k}r_{1}^{*} \\ -i\omega_{k}r_{2}^{*} \\ -i\omega_{k}r_{3}^{*} \end{array}\displaystyle \right ). $$

(3.16)

Therefore, we can easily obtain

$$r_{1}^{*}=\frac{a_{1}+i\omega_{k}}{b_{1}+i\omega_{k}},\qquad r_{2}^{*}= \frac{a_{1}+i\omega_{k}}{c_{1}+i\omega_{k}},\qquad r_{3}^{*}=-\frac{a_{1}+i\omega_{k}}{d_{1}e^{-i\omega_{k}\tau_{k}^{(j)}}}. $$

In the sequel, we shall verify that $\langle q^{*}(s), q(\theta)\rangle=1$. In fact, from (3.11), we have

$$\begin{aligned} \bigl\langle q^{*}(s), q(\theta)\bigr\rangle =&\bar{D}\bigl(1, \bar{r}_{1}^{*}, \bar{r}_{2}^{*}, \bar{r}_{3}^{*}\bigr) (1, r_{1}, r_{2}, r_{3})^{T} \\ &{}- \int_{-\tau_{k}^{(j)}}^{0} \int_{\xi=0}^{\theta}\bar{D}\bigl(1, \bar{r}_{1}^{*}, \bar{r}_{2}^{*}, \bar{r}_{3}^{*}\bigr) e^{-i\omega_{k}(\xi-\theta)} \,d\eta( \theta) (1, r_{1}, r_{2}, r_{3})^{T}e^{i\omega_{k}\xi} \,d\xi \\ =&\bar{D} \Biggl[1+\sum_{i=1}^{3}r_{i} \bar{r}_{i}^{*}- \int_{-\tau_{k}^{(j)}}^{0}\bigl(1, \bar{r}_{1}^{*}, \bar{r}_{2}^{*}, \bar{r}_{3}^{*}\bigr){\theta}e^{i\omega_{k}\theta}\,d \eta(\theta) (1, r_{1}, r_{2}, r_{3})^{T} \Biggr] \\ =&\bar{D} \Biggl\{ 1+\sum_{i=1}^{3}r_{i} \bar{r}_{i}^{*}+\bigl(1, \bar{r}_{1}^{*}, \bar{r}_{2}^{*}, \bar{r}_{3}^{*}\bigr) B_{1}e^{-i\omega_{k}\tau_{k}^{(j)}}(1, r_{1}, r_{2}, r_{3})^{T} \Biggr\} \\ =&\bar{D} \Biggl[1+\sum_{i=1}^{3}r_{i} \bar{r}_{i}^{*}+(1+r_{1}+r_{2}+r_{3})d_{1} \bar {r}_{3}^{*}e^{-i\omega_{k}\tau_{k}^{(j)}} \Biggr]=1. \end{aligned}$$

 □

Next, we use the same notations as those in Hassard et al. [15], and we first compute the coordinates to describe the center manifold $C_{0}$ at $\mu=0$. Let $y_{t}$ be the solution of equation (1.4) when $\mu=0$.

Define

$$ z(t)=\bigl\langle q^{*}, y_{t}\bigr\rangle , \qquad W(t, \theta)=y_{t}(\theta)-2\operatorname{Re}\bigl\{ z(t)q(\theta)\bigr\} $$

(3.17)

on the center manifold $C_{0}$, and we have

$$ W(t, \theta)=W\bigl(z(t), \bar{z}(t), \theta\bigr), $$

(3.18)

where

$$ W\bigl(z(t), \bar{z}(t), \theta\bigr)=W(z, \bar{z})=W_{20} \frac{z^{2}}{2}+W_{11}z\bar{z}+W_{02} \frac{\bar{z}^{2}}{2}+ \cdots $$

(3.19)

and z and z̄ are local coordinates for center manifold $C_{0}$ in the direction of $q^{*}$ and $\bar{q}^{*}$. Noting that W is also real if $y_{t}$ is real, we consider only real solutions. For solutions $y_{t}\in{C_{0}}$ of (1.4),

$$\begin{aligned} \dot{z}(t) =&\bigl\langle q^{*}(s), \dot{x}_{t}\bigr\rangle =\bigl\langle q^{*}(s), A(0)u_{t}+R(0)u_{t}\bigr\rangle \\ =&\bigl\langle q^{*}(s), A(0)y_{t}\bigr\rangle +\bigl\langle q^{*}(s), R(0)y_{t}\bigr\rangle \\ =&\bigl\langle A^{*}q^{*}(s), y_{t}\bigr\rangle +\bar{q}^{*}(0)R(0)y_{t} \\ &- \int_{-\tau_{k}^{(j)}}^{0} \int_{\xi=0}^{\theta} \bar{q}^{*}(\xi-\theta)\,d\eta( \theta)A(0)R(0)y_{t}(\xi)\,d\xi \\ =&\bigl\langle i\omega_{k}q^{*}(s), y_{t}\bigr\rangle + \bar{q}^{*}(0)f\bigl(0, y_{t}(\theta)\bigr) \\ \stackrel{\mathrm{def}}{=}&i\omega_{k}z(t)+\bar{q}^{*}(0)f_{0} \bigl(z(t), \bar{z}(t)\bigr). \end{aligned}$$

(3.20)

That is,

$$ \dot{z}(t)=i\omega_{k}{z}+g(z, \bar{z}), $$

(3.21)

where

$$ g(z, \bar{z})=g_{20}\frac{z^{2}}{2}+g_{11}z \bar{z}+g_{02} \frac{\bar{z}^{2}}{2}+g_{21}\frac{z^{2}\bar{z}}{2}+ \cdots. $$

(3.22)

Hence, we have

$$\begin{aligned} g(z, \bar{z}) =&\bar{q}^{*}(0)f_{0}(z, \bar{z})=f(0, y_{t}) \\ =&\bar{D}\bigl(1, \bar{r}_{1}^{*}, \bar{r}_{2}^{*}, \bar{r}_{3}^{*}\bigr) \bigl(f_{1}(0, y_{t}), f_{2}(0, y_{t}), f_{3}(0, y_{t}), f_{4}(0, y_{t})\bigr)^{T}, \end{aligned}$$

(3.23)

where

$$\begin{aligned}& f_{1}(0,y_{t}) = a_{3}y_{1t}^{2}(0)+a_{4}y_{1t}(0)y_{1t} \bigl(-\tau _{k}^{(j)}\bigr)+a_{5}y_{1t}(0)y_{4t}(0)+a_{6}y_{1t} \bigl(-\tau _{k}^{(j)}\bigr)y_{4t}(0) \\& \hphantom{f_{1}(0,y_{t}) ={}}{}+a_{7}y_{1t}^{3}(0)+a_{8}y_{1t}^{2}(0)y_{1t} \bigl(-\tau _{k}^{(j)}\bigr)+a_{9}y_{1t}^{2}(0)y_{4t}(0) \\& \hphantom{f_{1}(0,y_{t}) ={}}{}+a_{10}y_{1t}(0)y_{1t} \bigl(-\tau _{k}^{(j)}\bigr)y_{4t}(0)+ \mathrm{h.o.t.}, \\& f_{2}(0,y_{t}) = b_{3}y_{2t}^{2}(0)+b_{4}y_{2t}(0)y_{2t} \bigl(-\tau _{k}^{(j)}\bigr)+b_{5}y_{2t}(0)y_{4t}(0)+b_{6}y_{2t} \bigl(-\tau _{k}^{(j)}\bigr)y_{4t}(0) \\& \hphantom{f_{2}(0,y_{t}) ={}}{}+b_{7}y_{2t}^{3}(0)+b_{8}y_{2t}^{2}(0)y_{2t} \bigl(-\tau _{k}^{(j)}\bigr)+b_{9}y_{2t}^{2}(0)y_{4t}(0) \\& \hphantom{f_{2}(0,y_{t}) ={}}{}+b_{10}y_{2t}(0)y_{2t} \bigl(-\tau _{k}^{(j)}\bigr)y_{4t}(0)+ \mathrm{h.o.t.}, \\& f_{3}(0,y_{t}) = c_{3}y_{3t}^{2}(0)+c_{4}y_{3t}(0)y_{3t} \bigl(-\tau _{k}^{(j)}\bigr)+c_{5}y_{3t}(0)y_{4t}(0)+c_{6}y_{3t} \bigl(-\tau _{k}^{(j)}\bigr)y_{4t}(0) \\& \hphantom{f_{3}(0,y_{t}) ={}}{}+c_{7}y_{3t}^{3}(0)+c_{8}y_{3t}^{2}(0)y_{3t} \bigl(-\tau _{k}^{(j)}\bigr)+c_{9}y_{3t}^{2}(0)y_{4t}(0) \\& \hphantom{f_{3}(0,y_{t}) ={}}{}+c_{10}y_{3t}(0)y_{3t} \bigl(-\tau _{k}^{(j)}\bigr)y_{4t}(0)+ \mathrm{h.o.t.}, \\& f_{4}(0,y_{t}) = d_{1}y_{1t}\bigl(- \tau_{k}^{(j)}\bigr)y_{4t}(0)+d_{1}y_{2t} \bigl(-\tau _{k}^{(j)}\bigr)y_{4t}(0)+d_{1}y_{3t} \bigl(-\tau_{k}^{(j)}\bigr)y_{4t}(0). \end{aligned}$$

Noticing that

$$y_{t}(\theta)=\bigl(y_{1t}(\theta), y_{2t}( \theta), y_{3t}(\theta ),y_{4t}(\theta)\bigr)^{T} =W(t,\theta)+zq(\theta)+\bar{z}\bar{q} $$

and

$$q(\theta)=(1, r_{1}, r_{2}, r_{3})^{T}e^{i\omega_{k}\theta}, $$

we have

$$\begin{aligned}& y_{1t}(0) = z+\bar{z}+W_{20}^{(1)}(0) \frac{z^{2}}{2}+W_{11}^{(1)}(0)z\bar {z}+W_{02}^{(1)}(0) \frac{\bar{z}^{2}}{2}+\cdots, \\& y_{2t}(0) = r_{1}z+\bar{r}_{1} \bar{z}+W_{20}^{(2)}(0)\frac{z^{2}}{2} +W_{11}^{(2)}(0)z \bar{z}+W_{02}^{(2)}(0)\frac{\bar{z}^{2}}{2}+\cdots, \\& y_{3t}(0) = r_{2}z+\bar{r}_{2} \bar{z}+W_{20}^{(3)}(0)\frac {z^{2}}{2}+W_{11}^{(3)}(0)z \bar{z} +W_{02}^{(3)}(0)\frac{\bar{z}^{2}}{2}+\cdots, \\& y_{4t}(0) = r_{3}z+\bar{r}_{3} \bar{z}+W_{20}^{(4)}(0)\frac {z^{2}}{2}+W_{11}^{(4)}(0)z \bar{z} +W_{02}^{(4)}(0)\frac{\bar{z}^{2}}{2}+\cdots, \\& y_{1t}\bigl(-\tau_{k}^{(j)}\bigr) = e^{-i\omega_{k}\tau_{k}^{(j)}}z+e^{i\omega_{k}\tau _{k}^{(j)}}\bar{z} +W_{20}^{(1)}\bigl(- \tau_{k}^{(j)}\bigr)\frac{z^{2}}{2} \\& \hphantom{y_{1t}\bigl(-\tau_{k}^{(j)}\bigr) ={}}{}+W_{11}^{(1)} \bigl(-\tau _{k}^{(j)}\bigr)z\bar{z}+W_{02}^{(1)} \bigl(-\tau_{k}^{(j)}\bigr)\frac{\bar{z}^{2}}{2}+\cdots, \\& y_{2t}\bigl(-\tau_{k}^{(j)}\bigr) = r_{1}e^{-i\omega_{k}\tau_{k}^{(j)}}z+\bar {r}_{1}e^{i\omega_{k}\tau_{k}^{(j)}}\bar{z} +W_{20}^{(2)}\bigl(-\tau_{k}^{(j)}\bigr) \frac{z^{2}}{2} \\& \hphantom{y_{2t}\bigl(-\tau_{k}^{(j)}\bigr) ={}}{}+W_{11}^{(2)}\bigl(-\tau _{k}^{(j)} \bigr)z\bar{z}+W_{02}^{(2)}\bigl(-\tau_{k}^{(j)} \bigr)\frac{\bar{z}^{2}}{2}+\cdots , \\& y_{3t}\bigl(-\tau_{k}^{(j)}\bigr) = r_{2}e^{-i\omega_{k}\tau_{k}^{(j)}}z+\bar {r}_{2}e^{i\omega_{k}\tau_{k}^{(j)}}\bar{z} +W_{20}^{(3)}\bigl(-\tau_{k}^{(j)}\bigr) \frac{z^{2}}{2} \\& \hphantom{y_{3t}\bigl(-\tau_{k}^{(j)}\bigr) ={}}{}+W_{11}^{(3)}\bigl(-\tau _{k}^{(j)} \bigr)z\bar{z}+W_{02}^{(3)}\bigl(-\tau_{k}^{(j)} \bigr)\frac{\bar{z}^{2}}{2}+\cdots , \\& y_{4t}\bigl(-\tau_{k}^{(j)}\bigr) = r_{3}e^{-i\omega_{k}\tau_{k}^{(j)}}z+\bar {r}_{3}e^{i\omega_{k}\tau_{k}^{(j)}}\bar{z} +W_{20}^{(4)}\bigl(-\tau_{k}^{(j)}\bigr) \frac{z^{2}}{2} \\& \hphantom{y_{4t}\bigl(-\tau_{k}^{(j)}\bigr) ={}}{}+W_{11}^{(4)}\bigl(-\tau _{k}^{(j)} \bigr)z\bar{z}+W_{02}^{(4)}\bigl(-\tau_{k}^{(j)} \bigr)\frac{\bar{z}^{2}}{2}+\cdots. \end{aligned}$$

From (3.22) and (3.23), we have

$$\begin{aligned} g(z, \bar{z}) =&\bar{q}^{*}(0)f_{0}(z,\bar{z}) \\ =&\bar{D} \bigl[f_{1}(0, y_{t})+\bar{r}_{1}^{*}f_{2}(0, x_{t})+\bar{r}_{2}^{*}f_{3}(0, y_{t})+ \bar{r}_{3}^{*}f_{4}(0, y_{t}) \bigr] \\ =&\bar{D} \bigl[a_{3}+a_{4}e^{-i\omega_{k}\tau _{k}^{(j)}}+a_{5}r_{3}+a_{6}r_{3}e^{-i\omega_{k}\tau_{k}^{(j)}} \\ &{}+\bar{r}_{1}^{*} \bigl(b_{3}r_{1}^{2}+b_{4}r_{1}^{2}e^{-i\omega_{k}\tau _{k}^{(j)}}+b_{5}r_{1}r_{3}+b_{6}r_{1}r_{3}e^{-i\omega_{k}\tau_{k}^{(j)}} \bigr) \\ &{}+\bar{r}_{2}^{*} \bigl(c_{3}r_{2}^{2}+c_{4}r_{2}^{2}e^{-i\omega_{k}\tau _{k}^{(j)}}+c_{5}r_{2}r_{3}+c_{6}r_{2}r_{3}e^{-i\omega_{k}\tau_{k}^{(j)}} \bigr) \\ &{} +\bar{r}_{3}^{*} \bigl(d_{1}r_{3}e^{-i\omega_{k}\tau _{k}^{(j)}}+d_{1}r_{1}r_{3}e^{-i\omega_{k}\tau_{k}^{(j)}}+d_{1}r_{2}r_{3}e^{-i\omega_{k}\tau _{k}^{(j)}} \bigr) \bigr]z^{2} \\ &{}+\bar{D} \bigl[2a_{3}+2a_{4}\operatorname{Re}\bigl\{ r_{3}e^{i\omega_{k}\tau_{k}^{(j)}}\bigr\} +2a_{5}\operatorname{Re} \{r_{3}\}+2a_{6}\operatorname{Re}\bigl\{ r_{3}e^{i\omega_{k}\tau_{k}^{(j)}} \bigr\} \\ &{}+r_{1}^{*} \bigl(2b_{3}|r_{1}|^{2}+2b_{4} \operatorname{Re}\bigl\{ r_{1}\bar{r}_{1}e^{-i\omega_{k}\tau _{k}^{(j)}} \bigr\} +2b_{5}\operatorname{Re}\{r_{1}\bar{r}_{3} \}+2b_{6}\operatorname{Re}\bigl\{ r_{1}\bar {r}_{3}e^{-i\omega_{k}\tau_{k}^{(j)}}\bigr\} \bigr) \\ &{}+r_{2}^{*} \bigl(2c_{3}|r_{2}|^{2}+2c_{4} \operatorname{Re}\bigl\{ |r_{2}|^{2}e^{i\omega_{k}\tau _{k}^{(j)}}\bigr\} +2c_{5}\operatorname{Re}\{r_{2}\bar{r}_{3} \}+2c_{6}\operatorname{Re}\bigl\{ r_{2}\bar {r}_{3}e^{-i\omega_{k}\tau_{k}^{(j)}}\bigr\} \bigr) \\ &{} +r_{3}^{*} \bigl(2d_{1}\operatorname{Re}\bigl\{ r_{3}e^{i\omega_{k}\tau_{k}^{(j)}}\bigr\} +2d_{1}\operatorname{Re}\bigl\{ r_{1}e^{-i\omega_{k}\tau_{k}^{(j)}}\bigr\} +2d_{1}\operatorname{Re}\bigl\{ r_{2}e^{-i\omega_{k}\tau_{k}^{(j)}}\bigr\} \bigr) \bigr]z\bar{z} \\ &{}+\bar{D} \bigl[a_{3}+a_{4}e^{i\omega_{k}\tau_{k}^{(j)}}+a_{5} \bar{r}_{3}+a_{6}\bar {r}_{3}e^{i\omega_{k}\tau_{k}^{(j)}} \\ &{}+r_{1}^{*} \bigl(b_{3}\bar{r}_{1}^{2}+b_{4} \bar{r}_{1}^{2}e^{i\omega_{k}\tau _{k}^{(j)}}+b_{5} \bar{r}_{1}\bar{r}_{3}+b_{6}\bar{r}_{1} \bar{r}_{3}e^{i\omega_{k}\tau _{k}^{(j)}} \bigr) \\ &{}+r_{2}^{*} \bigl(c_{3}\bar{r}_{2}^{2}+c_{4} \bar{r}_{2}^{2}e^{i\omega_{k}\tau _{k}^{(j)}}+c_{5} \bar{r}_{2}r_{3}+c_{6}\bar{r}_{2} \bar{r}_{3}e^{i\omega_{k}\tau _{k}^{(j)}} \bigr) \\ &{} +r_{3} \bigl(d_{1}\bar{r}_{3}e^{i\omega_{k}\tau_{k}^{(j)}}+d_{1} \bar {r}_{1}\bar{r}_{3}e^{i\omega_{k}\tau_{k}^{(j)}}+d_{1} \bar{r}_{2}\bar{r}_{3}e^{i\omega _{k}\tau_{k}^{(j)}} \bigr) \bigr] \bar{z}^{2} \\ &{}+\bar{D} \biggl\{ r_{1}^{*} \biggl[b_{3} \bigl(2r_{1}W_{11}^{(2)}(0)+W_{201}^{(2)}(0) \bar{r}_{1} \bigr) \\ &{}+b_{4} \biggl(r_{1}W_{11}^{(2)} \bigl(-\tau_{k}^{(j)}\bigr)+\frac{1}{2}\bar {r}_{1}W_{20}^{(2)}\bigl(-\tau_{k}^{(j)} \bigr) \\ &{} +\frac{1}{2}\bar{r}_{1}W_{20}^{(2)}(0)e^{-i\omega_{k}\tau_{k}^{(j)}} +r_{1}W_{11}^{(2)}(0)e^{-i\omega_{k}\tau_{k}^{(j)}} \biggr)+b_{5} \biggl(r_{1}W_{11}^{(4)}(0)+ \frac{1}{2}\bar{r}_{1}W_{20}^{(4)}(0) \\ &{} +\frac{1}{2}\bar{r}_{3}W_{20}^{(2)}(0)+r_{3}W_{11}^{(2)}(0) \biggr) +b_{6} \biggl(r_{1}W_{11}^{(4)}(0)+ \frac{1}{2}\bar {r}_{1}W_{20}^{(4)}(0)e^{i\omega_{k}\tau_{k}^{(j)}} \\ &{} +\frac{1}{2}\bar{r}_{3}W_{20}^{(2)}(- \tau)e^{i\omega_{k}\tau _{k}^{(j)}}+r_{3}W_{11}^{(2)}\bigl(- \tau_{k}^{(j)}\bigr) \biggr) \\ &{}+3b_{7}r_{1}^{2} \bar{r}_{1}+b_{8} \bigl(r_{1}^{2} \bar{r}_{1}e^{i\omega_{k}\tau _{k}^{(j)}}+2r_{1}^{2} \bar{r}_{1}e^{-i\omega_{k}\tau_{k}^{(j)}} \bigr) \\ &{} +b_{9}\bigl(r_{1}^{2}\bar{r}_{3}+2|r_{1}|^{2}r_{3} \bigr)+b_{10} \bigl(r_{1}^{2}e^{-i\omega _{k}\tau_{k}^{(j)}}+|r_{1}|^{2}r_{3}e^{i\omega_{k}\tau_{k}^{(j)}} +|r_{1}|^{2}r_{3}e^{-i\omega_{k}\tau_{k}^{(j)}} \bigr) \biggr] \\ &{}+r_{2}^{*} \biggl[3c_{3}r_{2}^{2} \bar{r}_{2}+c_{4} \biggl(r_{2}W_{11}^{(3)} \bigl(-\tau _{k}^{(j)}\bigr)+\frac{1}{2} \bar{r}_{2}W_{20}^{(3)}\bigl(-\tau_{k}^{(j)} \bigr) \\ &{}+\frac{1}{2}\bar{r}_{2}W_{20}^{(3)} \bigl(-\tau_{k}^{(j)}\bigr)e^{i\omega_{k}\tau _{k}^{(j)}}+r_{2}W_{11}^{(3)}(0)e^{-i\omega_{k}\tau_{k}^{(j)}} \biggr) \\ &{} +c_{5} \biggl(r_{2}W_{11}^{(4)}(0)+ \frac{1}{2}\bar{r}_{2}W_{20}^{(4)}(0) + \frac{1}{2}\bar{r}_{3}W_{20}^{(3)}(0)+r_{3}W_{11}^{(3)}(0) \biggr) \\ &{}+c_{6} \biggl(r_{2}W_{11}^{(4)}(0)e^{-i\omega_{k}\tau_{k}^{(j)}}+ \frac {1}{2}\bar{r}_{2}W_{20}^{(4)}(0)e^{i\omega_{k}\tau_{k}^{(j)}} \\ &{}+\frac{1}{2}\bar{r}_{3}W_{20}^{(3)}\bigl(- \tau_{k}^{(j)}\bigr)+r_{3}W_{11}^{(3)} \bigl(-\tau _{k}^{(j)}\bigr) \biggr) \\ &{}+3c_{7}r_{2}^{2}\bar{r}_{2}+c_{8} \bigl(r_{2}^{2}\bar{r}_{2}e^{i\omega_{k}\tau _{k}^{(j)}}+2r_{2}^{2} \bar{r}_{2}e^{-i\omega_{k}\tau_{k}^{(j)}} \bigr) \\ &{}+c_{9} \bigl(r_{2}^{2}\bar{r}_{3}+2|r_{2}|^{2}r_{3} \bigr)+c_{10} \bigl(r_{2}^{2}\bar {r}_{3}e^{-i\omega_{k}\tau_{k}^{(j)}} \\ &{} +|r_{2}|^{2}r_{3}e^{-i\omega_{k}\tau _{k}^{(j)}}+|r_{2}|^{2}r_{3}e^{i\omega_{k}\tau_{k}^{(j)}} \bigr) \biggr] +\bar{r}_{3}^{*}d_{1}\biggl[W_{11}^{(4)}(0)+ \frac{1}{2}W_{20}^{(4)}(0)+\frac {1}{2} \bar{r}_{3}W_{20}^{(1)}(0) \\ &{}+r_{3}W_{11}^{(1)}(0)+r_{1}W_{11}^{(4)}(0)e^{-i\omega_{k}\tau _{k}^{(j)}}+ \frac{1}{2}\bar{r}_{1}W_{20}^{(4)}(0)e^{i\omega_{k}\tau_{k}^{(j)}} \\ &{}+\frac{1}{2}\bar{r}_{3}W_{20}^{(4)}\bigl(- \tau_{k}^{(j)}\bigr)+r_{3}W_{11}^{(2)} \bigl(-\tau _{k}^{(j)}\bigr)+r_{2}W_{11}^{(4)}(0)e^{-i\omega_{k}\tau_{k}^{(j)}} \\ &{}+ \frac{1}{2}\bar {r}_{2}W_{20}^{(4)}(0)e^{i\omega_{k}\tau_{k}^{(j)}} +\frac{1}{2}\bar{r}_{3}W_{20}^{(3)}\bigl(- \tau_{k}^{(j)}\bigr)e^{i\omega_{k}\tau _{k}^{(j)}}+r_{3}W_{11}^{(3)} \bigl(-\tau_{k}^{(j)}\bigr)\biggr]z^{2}\bar{z}+\cdots \biggr\} \end{aligned}$$

and we obtain

$$\begin{aligned}& g_{20} = 2\bar{D}\bigl[a_{3}+a_{4}e^{-i\omega_{k}\tau _{k}^{(j)}}+a_{5}r_{3}+a_{6}r_{3}e^{-i\omega_{k}\tau_{k}^{(j)}} \\ & \hphantom{g_{20} ={}}{}+\bar{r}_{1}^{*}\bigl(b_{3}r_{1}^{2}+b_{4}r_{1}^{2}e^{-i\omega_{k}\tau _{k}^{(j)}}+b_{5}r_{1}r_{3}+b_{6}r_{1}r_{3}e^{-i\omega_{k}\tau_{k}^{(j)}} \bigr) \\& \hphantom{g_{20} ={}}{}+\bar{r}_{2}^{*}\bigl(c_{3}r_{2}^{2}+c_{4}r_{2}^{2}e^{-i\omega_{k}\tau _{k}^{(j)}}+c_{5}r_{2}r_{3}+c_{6}r_{2}r_{3}e^{-i\omega_{k}\tau_{k}^{(j)}} \bigr) \\& \hphantom{g_{20} ={}}{}+\bar{r}_{3}^{*}\bigl(d_{1}r_{3}e^{-i\omega_{k}\tau _{k}^{(j)}}+d_{1}r_{1}r_{3}e^{-i\omega_{k}\tau_{k}^{(j)}}+d_{1}r_{2}r_{3}e^{-i\omega_{k}\tau _{k}^{(j)}} \bigr)\bigr], \\& g_{11} = \bar{D}\bigl[2a_{3}+2a_{4} \operatorname{Re}\bigl\{ r_{3}e^{i\omega_{k}\tau _{k}^{(j)}}\bigr\} +2a_{5} \operatorname{Re}\{r_{3}\}+2a_{6}\operatorname{Re}\bigl\{ r_{3}e^{i\omega_{k}\tau _{k}^{(j)}}\bigr\} \\& \hphantom{g_{11} ={}}{}+r_{1}^{*}\bigl(2b_{3}|r_{1}|^{2}+2b_{4} \operatorname{Re}\bigl\{ r_{1}\bar{r}_{1}e^{-i\omega_{k}\tau _{k}^{(j)}} \bigr\} +2b_{5}\operatorname{Re}\{r_{1}\bar{r}_{3} \}+2b_{6}\operatorname{Re}\bigl\{ r_{1}\bar {r}_{3}e^{-i\omega_{k}\tau_{k}^{(j)}}\bigr\} \bigr) \\& \hphantom{g_{11} ={}}{}+r_{2}^{*}\bigl(2c_{3}|r_{2}|^{2}+2c_{4} \operatorname{Re}\bigl\{ |r_{2}|^{2}e^{i\omega_{0}\tau _{k}^{(j)}}\bigr\} +2c_{5}\operatorname{Re}\{r_{2}\bar{r}_{3} \}+2c_{6}\operatorname{Re}\bigl\{ r_{2}\bar {r}_{3}e^{-i\omega_{k}\tau_{k}^{(j)}}\bigr\} \bigr) \\& \hphantom{g_{11} ={}}{}+r_{3}^{*}\bigl(2d_{1}\operatorname{Re}\bigl\{ r_{3}e^{i\omega_{k}\tau_{k}^{(j)}}\bigr\} +2d_{1}\operatorname{Re}\bigl\{ r_{1}e^{-i\omega_{k}\tau_{k}^{(j)}}\bigr\} +2d_{1}\operatorname{Re}\bigl\{ r_{2}e^{-i\omega_{k}\tau_{k}^{(j)}}\bigr\} \bigr)\bigr], \\& g_{02} = 2\bar{D}\bigl[a_{3}+a_{4}e^{i\omega_{k}\tau_{k}^{(j)}}+a_{5} \bar {r}_{3}+a_{6}\bar{r}_{3}e^{i\omega_{k}\tau_{k}^{(j)}} \\& \hphantom{g_{02} ={}}{}+r_{1}^{*}\bigl(b_{3}\bar{r}_{1}^{2}+b_{4} \bar{r}_{1}^{2}e^{i\omega_{k}\tau _{k}^{(j)}}+b_{5} \bar{r}_{1}\bar{r}_{3}+b_{6}\bar{r}_{1} \bar{r}_{3}e^{i\omega_{k}\tau _{k}^{(j)}}\bigr) \\& \hphantom{g_{02} ={}}{}+r_{2}^{*}\bigl(c_{3}\bar{r}_{2}^{2}+c_{4} \bar{r}_{2}^{2}e^{i\omega_{k}\tau _{k}^{(j)}}+c_{5} \bar{r}_{2}r_{3}+c_{6}\bar{r}_{2} \bar{r}_{3}e^{i\omega_{k}\tau _{k}^{(j)}}\bigr) \\& \hphantom{g_{02} ={}}{}+r_{3}\bigl(d_{1}\bar{r}_{3}e^{i\omega_{k}\tau_{k}^{(j)}}+d_{1} \bar {r}_{1}\bar{r}_{3}e^{i\omega_{k}\tau_{k}^{(j)}}+d_{1} \bar{r}_{2}\bar{r}_{3}e^{i\omega _{k}\tau_{k}^{(j)}}\bigr)\bigr], \\& g_{21} = 2\bar{D} \biggl\{ r_{1}^{*}\biggl[b_{3} \bigl(2r_{1}W_{11}^{(2)}(0)+W_{201}^{(2)}(0) \bar{r}_{1}\bigr) +b_{4}\biggl(r_{1}W_{11}^{(2)} \bigl(-\tau_{k}^{(j)}\bigr)+\frac{1}{2}\bar {r}_{1}W_{20}^{(2)}\bigl(-\tau_{k}^{(j)} \bigr) \\& \hphantom{g_{21} ={}}{}+\frac{1}{2}\bar{r}_{1}W_{20}^{(2)}(0)e^{-i\omega_{k}\tau_{k}^{(j)}} +r_{1}W_{11}^{(2)}(0)e^{-i\omega_{k}\tau_{k}^{(j)}} \biggr)+b_{5} \biggl(r_{1}W_{11}^{(4)}(0)+ \frac{1}{2}\bar{r}_{1}W_{20}^{(4)}(0) \\& \hphantom{g_{21} ={}}{}+\frac{1}{2}\bar{r}_{3}W_{20}^{(2)}(0)+r_{3}W_{11}^{(2)}(0) \biggr) +b_{6}\biggl(r_{1}W_{11}^{(4)}(0)+ \frac{1}{2}\bar {r}_{1}W_{20}^{(4)}(0)e^{i\omega_{k}\tau_{k}^{(j)}} \\& \hphantom{g_{21} ={}}{}+\frac{1}{2}\bar{r}_{3}W_{20}^{(2)} \bigl(-\tau_{k}^{(j)}\bigr)e^{i\omega _{k}\tau_{k}^{(j)}}+r_{3}W_{11}^{(2)} \bigl(-\tau_{k}^{(j)}\bigr)\biggr) \\& \hphantom{g_{21} ={}}{}+3b_{7}r_{1}^{2} \bar{r}_{1}+b_{8}\bigl(r_{1}^{2} \bar{r}_{1}e^{i\omega_{k}\tau _{k}^{(j)}}+2r_{1}^{2} \bar{r}_{1}e^{-i\omega_{k}\tau_{k}^{(j)}}\bigr) \\& \hphantom{g_{21} ={}}{}+b_{9}\bigl(r_{1}^{2} \bar{r}_{3}+2|r_{1}|^{2}r_{3} \bigr)+b_{10}\bigl(r_{1}^{2}e^{-i\omega _{k}\tau_{k}^{(j)}}+|r_{1}|^{2}r_{3}e^{i\omega_{k}\tau_{k}^{(j)}} +|r_{1}|^{2}r_{3}e^{-i\omega_{k}\tau_{k}^{(j)}}\bigr)\biggr] \\& \hphantom{g_{21} ={}}{}+r_{2}^{*}\biggl[3c_{3}r_{2}^{2} \bar{r}_{2}+c_{4}\biggl(r_{2}W_{11}^{(3)} \bigl(-\tau _{k}^{(j)}\bigr)+\frac{1}{2} \bar{r}_{2}W_{20}^{(3)}\bigl(-\tau_{k}^{(j)} \bigr) +\frac{1}{2}\bar{r}_{2}W_{20}^{(3)}(- \tau)e^{i\omega_{k}\tau_{k}^{(j)}} \\& \hphantom{g_{21} ={}}{}+r_{2}W_{11}^{(3)}(0)e^{-i\omega_{k}\tau_{k}^{(j)}} \biggr)+c_{5} \biggl(r_{2}W_{11}^{(4)}(0)+ \frac{1}{2}\bar{r}_{2}W_{20}^{(4)}(0) + \frac{1}{2}\bar{r}_{3}W_{20}^{(3)}(0)+r_{3}W_{11}^{(3)}(0) \biggr) \\& \hphantom{g_{21} ={}}{}+c_{6}\biggl(r_{2}W_{11}^{(4)}(0)e^{-i\omega_{k}\tau_{k}^{(j)}}+ \frac {1}{2}\bar{r}_{2}W_{20}^{(4)}(0)e^{i\omega_{k}\tau_{k}^{(j)}} +\frac{1}{2}\bar{r}_{3}W_{20}^{(3)}\bigl(- \tau_{k}^{(j)}\bigr)+r_{3}W_{11}^{(3)} \bigl(-\tau _{k}^{(j)}\bigr)\biggr) \\& \hphantom{g_{21} ={}}{}+3c_{7}r_{2}^{2} \bar{r}_{2}+c_{8}\bigl(r_{2}^{2} \bar{r}_{2}e^{i\omega_{k}\tau _{k}^{(j)}}+2r_{2}^{2} \bar{r}_{2}e^{-i\omega_{k}\tau_{k}^{(j)}}\bigr) +c_{9}\bigl(r_{2}^{2} \bar{r}_{3}+2|r_{2}|^{2}r_{3} \bigr)+c_{10}\bigl(r_{2}^{2}\bar {r}_{3}e^{-i\omega_{k}\tau_{k}^{(j)}} \\& \hphantom{g_{21} ={}}{}+|r_{2}|^{2}r_{3}e^{-i\omega_{k}\tau _{k}^{(j)}}+|r_{2}|^{2}r_{3}e^{i\omega_{k}\tau_{k}^{(j)}} \bigr)\biggr] +\bar{r}_{3}^{*}d_{1}\biggl[W_{11}^{(4)}(0)+ \frac{1}{2}W_{20}^{(4)}(0)+\frac {1}{2} \bar{r}_{3}W_{20}^{(1)}(0) \\& \hphantom{g_{21} ={}}{}+r_{3}W_{11}^{(1)}(0)+r_{1}W_{11}^{(4)}(0)e^{-i\omega_{k}\tau _{k}^{(j)}}+ \frac{1}{2}\bar{r}_{1}W_{20}^{(4)}(0)e^{i\omega_{k}\tau_{k}^{(j)}} \\& \hphantom{g_{21} ={}}{}+\frac{1}{2}\bar{r}_{3}W_{20}^{(4)}\bigl(- \tau_{k}^{(j)}\bigr)+r_{3}W_{11}^{(2)} \bigl(-\tau _{k}^{(j)}\bigr)+r_{2}W_{11}^{(4)}(0)e^{-i\omega_{k}\tau_{k}^{(j)}} \\& \hphantom{g_{21} ={}}{}+ \frac{1}{2}\bar {r}_{2}W_{20}^{(4)}(0)e^{i\omega_{k}\tau_{k}^{(j)}} +\frac{1}{2}\bar{r}_{3}W_{20}^{(3)}\bigl(- \tau_{k}^{(j)}\bigr)e^{i\omega_{k}\tau _{k}^{(j)}}+r_{3}W_{11}^{(3)} \bigl(-\tau_{k}^{(j)}\bigr)\biggr]\biggr\} . \end{aligned}$$

For

$$\begin{aligned}& W_{20}^{(2)}(0), \qquad W_{11}^{(2)}(0), \qquad W_{11}^{(2)}\bigl(-\tau_{k}^{(j)} \bigr),\qquad W_{20}^{(2)}\bigl(-\tau_{k}^{(j)} \bigr),\qquad W_{11}^{(4)}(0),\qquad W_{20}^{(4)}(0), \\& W_{11}^{(4)}(0),\qquad W_{20}^{(4)}(0), \qquad W_{11}^{(2)}\bigl(-\tau_{k}^{(j)} \bigr),\qquad W_{11}^{(3)}\bigl(-\tau_{k}^{(j)}\bigr), \qquad W_{11}^{(2)}(0),\qquad W_{20}^{(3)}(0), \\& W_{11}^{(3)}(0),\qquad W_{11}^{(4)}(0), \qquad W_{20}^{(3)}\bigl(-\tau_{k}^{(j)} \bigr),\qquad W_{11}^{(3)}\bigl(-\tau_{k}^{(j)} \bigr),\qquad W_{20}^{(3)}\bigl(-\tau_{k}^{(j)} \bigr) \end{aligned}$$

unknown in $g_{21}$, we still need to compute them.

From (3.9), (3.23), we have

$$\begin{aligned} W' =&\left \{ \textstyle\begin{array}{l@{\quad}l} AW-2\operatorname{Re}{\{\bar{q}^{*}(0)f_{0}q(\theta)\}}, &-\tau_{k}^{(j)}\leq \theta< 0, \\ AW-2\operatorname{Re}{\{\bar{q}^{*}(0)f_{0}q(\theta)\}}+f_{0}, &\theta=0 \end{array}\displaystyle \right . \\ \stackrel{\mathrm{def}}{=}&AW+H(z, \bar{z}, \theta), \end{aligned}$$

(3.24)

where

$$ H(z,\bar{z},\theta)=H_{20}(\theta)\frac{z^{2}}{2}+H_{11}( \theta)z\bar {z}+H_{02}(\theta) \frac{\bar{z}^{2}}{2}+\cdots. $$

(3.25)

Comparing the coefficients, we obtain

$$\begin{aligned}& (A-2i\omega_{0})W_{20}(\theta)=-H_{20}( \theta), \end{aligned}$$

(3.26)

$$\begin{aligned}& AW_{11}(\theta)=-H_{11}(\theta), \\& \ldots. \end{aligned}$$

(3.27)

And we know that for $\theta\in[-\tau_{k}^{(j)}, 0)$,

$$ H(z,\bar{z}, \theta)=-\bar{q}^{*}(0)f_{0}q(\theta)-q^{*}(0) \bar{f}_{0}\bar{q}(\theta) =-g(z, \bar{z})q(\theta)-\bar{g}(z, \bar{z}) \bar{q}(\theta). $$

(3.28)

Comparing the coefficients of (3.25) with (3.28) gives

$$\begin{aligned}& H_{20}(\theta)=-g_{20}q(\theta)- \bar{g}_{02}\bar{q}(\theta), \end{aligned}$$

(3.29)

$$\begin{aligned}& H_{11}(\theta)=-g_{11}q(\theta)-\bar{g}_{11} \bar{q}(\theta). \end{aligned}$$

(3.30)

From (3.26), (3.29), and the definition of A, we get

$$ \dot{W}_{20}(\theta)=2i\omega_{k}W_{20}( \theta)+g_{20}q(\theta) +\bar{g}_{02}\bar{q}(\theta). $$

(3.31)

Noting that $q(\theta)=q(0)e^{i\omega_{0}\theta}$, we have

$$ W_{20}(\theta)=\frac{ig_{20}}{\omega_{k}}q(0) e^{i\omega_{k}\theta}+ \frac{i\bar{g}_{02}}{3\omega_{k}} \bar{q}(0)e^{-i\omega_{k}\theta} +E_{1}e^{2i\omega_{k}\theta}, $$

(3.32)

where $E_{1}$ is a constant vector. Similarly, from (3.27), (3.30), and the definition of A, we have

$$\begin{aligned}& \dot{W}_{11}(\theta)=g_{11}q(\theta) +\bar{g}_{11} \bar{q}(\theta), \end{aligned}$$

(3.33)

$$\begin{aligned}& W_{11}(\theta)=-\frac{ig_{11}}{\omega_{k}}q(0) e^{i\omega_{k}\theta}+ \frac{i\bar{g}_{11}}{\omega_{k}} \bar{q}(0)e^{-i\omega_{k}\theta}+E_{2}, \end{aligned}$$

(3.34)

where $E_{2}$ is a constant vector.

In the following, we shall seek appropriate $E_{1}$, $E_{2}$ in (3.32), (3.34), respectively. It follows from the definition of A and (3.29), (3.30) that

$$ \int_{-\tau_{k}^{(j)}}^{0}d\eta(\theta)W_{20}(\theta)= 2i\omega_{k}W_{20}(0)-H_{20}(0) $$

(3.35)

and

$$ \int_{-\tau_{k}^{(j)}}^{0}d\eta(\theta)W_{11}( \theta)=-H_{11}(0), $$

(3.36)

where $\eta(\theta)=\eta(0, \theta)$.

From (3.30), we have

$$ H_{20}(0)=-g_{20}q(0)-\bar{g}_{02} \bar{q}(0)+(H_{1}, H_{2}, H_{3}, H_{4})^{T}, $$

(3.37)

where

$$\begin{aligned}& H_{1}=2\bigl(a_{3}+a_{4}e^{-i\omega_{k}\tau_{k}^{(j)}}+a_{5}r_{3}+a_{6}r_{3}e^{-i\omega_{k}\tau _{k}^{(j)}} \bigr), \\& H_{2}=2 \bigl(b_{3}r_{1}^{2}+b_{4}r_{1}^{2}e^{-i\omega_{k}\tau _{k}^{(j)}}+b_{5}r_{1}r_{3}+b_{6}r_{1}r_{3}e^{-i\omega_{k}\tau_{k}^{(j)}} \bigr), \\& H_{3}=2 \bigl(c_{3}r_{2}^{2}+c_{4}r_{2}^{2}e^{-i\omega_{k}\tau _{k}^{(j)}}+c_{5}r_{2}r_{3}+c_{6}r_{2}r_{3}e^{-i\omega_{k}\tau_{k}^{(j)}} \bigr), \\& H_{4}=2 \bigl(d_{1}r_{3}e^{-i\omega_{k}\tau_{k}^{(j)}}+d_{1}r_{1}r_{3}e^{-i\omega_{k}\tau _{k}^{(j)}}+d_{1}r_{2}r_{3}e^{-i\omega_{k}\tau_{k}^{(j)}} \bigr). \end{aligned}$$

From (3.31), we have

$$ H_{11}(0)=-g_{11}q(0)-\bar{g}_{11}(0) \bar{q}(0)+(P_{1}, P_{2}, P_{3}, P_{4})^{T}, $$

(3.38)

where

$$\begin{aligned}& P_{1}=2a_{3}+2a_{4}\operatorname{Re}\bigl\{ r_{3}e^{i\omega_{k}\tau_{k}^{(j)}}\bigr\} +2a_{5}\operatorname{Re}\{ r_{3}\}+2a_{6}\operatorname{Re}\bigl\{ r_{3}e^{i\omega_{k}\tau_{k}^{(j)}} \bigr\} , \\& P_{2}=2b_{3}|r_{1}|^{2}+2b_{4} \operatorname{Re}\bigl\{ r_{1}\bar{r}_{1}e^{-i\omega_{k}\tau _{k}^{(j)}} \bigr\} +2b_{5}\operatorname{Re}\{r_{1}\bar{r}_{3} \}+2b_{6}\operatorname{Re}\bigl\{ r_{1}\bar {r}_{3}e^{-i\omega_{k}\tau_{k}^{(j)}}\bigr\} , \\& P_{3}=2c_{3}|r_{2}|^{2}+2c_{4} \operatorname{Re}\bigl\{ |r_{2}|^{2}e^{i\omega_{k}\tau_{k}^{(j)}}\bigr\} +2c_{5}\operatorname{Re}\{r_{2}\bar{r}_{3} \}+2c_{6}\operatorname{Re}\bigl\{ r_{2}\bar{r}_{3}e^{-i\omega _{k}\tau_{k}^{(j)}} \bigr\} , \\& P_{4}=2d_{1}\operatorname{Re}\bigl\{ r_{3}e^{i\omega_{k}\tau_{k}^{(j)}} \bigr\} +2d_{1}\operatorname{Re}\bigl\{ r_{1}e^{-i\omega_{k}\tau_{k}^{(j)}} \bigr\} +2d_{1}\operatorname{Re}\bigl\{ r_{2}e^{-i\omega_{k}\tau _{k}^{(j)}} \bigr\} . \end{aligned}$$

From (3.26), (3.27), and the definition of A, we have

$$ \left \{ \textstyle\begin{array}{l} BW_{20}(0)+B_{1}W_{20}(-\tau_{k}^{(j)})=2i\omega_{k}W_{20}(0)-H_{20}(0), \\ BW_{11}(0)+B_{1}W_{11}(-\tau_{k}^{(j)})=-H_{11}(0). \end{array}\displaystyle \right . $$

(3.39)

Noting that

$$\begin{aligned}& \biggl(i\omega_{k}I- \int_{-\tau_{k}^{(j)}}^{0}e^{i\omega_{k}\theta} \,d\eta(\theta) \biggr)q(0)=0, \end{aligned}$$

(3.40)

$$\begin{aligned}& \biggl(-i\omega_{k}I- \int_{-\tau_{k}^{(j)}}^{0}e^{-i\omega_{k}\theta} \,d\eta(\theta) \biggr) \bar{q}(0)=0, \end{aligned}$$

(3.41)

and substituting (3.36) and (3.41) into (3.39), we have

$$ \biggl(2i\omega_{k}I- \int_{-\tau_{k}^{(j)}}^{0}e^{2i\omega_{k}\theta} \,d\eta(\theta) \biggr)E_{1}=(H_{1}, H_{2}, H_{3}, H_{4})^{T}. $$

(3.42)

That is,

$$ \det \left ( \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{}} 2i\omega_{k}-a_{1} & 0 & 0 & -a_{2} \\ 0 & 2i\omega_{k}-b_{1} & 0 & -b_{2} \\ 0 & 0 & 2i\omega_{k}-c_{1} & -c_{2} \\ -d_{1}e^{-2i\omega_{k}\tau_{k}^{(j)}} & -d_{1}e^{-2i\omega_{k}\tau_{k}^{(j)}} &-d_{1}e^{-2i\omega_{k}\tau_{k}^{(j)}} & 2i\omega_{k} \end{array}\displaystyle \right )\left ( \textstyle\begin{array}{@{}c@{}} E_{1}^{(1)} \\ E_{1}^{(2)} \\ E_{1}^{(3)} \\ E_{1}^{(4)} \end{array}\displaystyle \right )=\left ( \textstyle\begin{array}{@{}c@{}} H_{1} \\ H_{2} \\ H_{3} \\ H_{4} \end{array}\displaystyle \right ). $$

(3.43)

Hence,

$$ E_{1}^{(1)}=\frac{\Delta_{11}}{\Delta_{1}},\qquad E_{1}^{(2)}=\frac{\Delta _{12}}{\Delta_{1}},\qquad E_{1}^{(3)}= \frac{\Delta_{13}}{\Delta_{1}},\qquad E_{1}^{(4)}=\frac{\Delta _{14}}{\Delta_{1}}, $$

(3.44)

where

$$\begin{aligned}& \Delta_{1}=\det \left ( \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{}} 2i\omega_{k}-a_{1} & 0 & 0 & -a_{2} \\ 0 & 2i\omega_{k}-b_{1} & 0 & -b_{2} \\ 0 & 0 & 2i\omega_{k}-c_{1} & -c_{2} \\ -d_{1}e^{-2i\omega_{k}\tau_{k}^{(j)}} & -d_{1}e^{-2i\omega_{k}\tau_{k}^{(j)}} &-d_{1}e^{-2i\omega_{k}\tau_{k}^{(j)}} & 2i\omega_{k} \end{array}\displaystyle \right ), \\& \Delta_{11}=\det \left ( \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{}} H_{1} & 0 & 0 & -a_{2} \\ H_{2} & 2i\omega_{k}-b_{1} & 0 & -b_{2} \\ H_{3}1 & 0 & 2i\omega_{k}-c_{1} & -c_{2} \\ H_{4} & -d_{1}e^{-2i\omega_{k}\tau_{k}^{(j)}} &-d_{1}e^{-2i\omega_{k}\tau_{k}^{(j)}} & 2i\omega_{k} \end{array}\displaystyle \right ), \\& \Delta_{12}=\det \left ( \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{}} 2i\omega_{k}-a_{1} & H_{1} & 0 & -a_{2} \\ 0 & H_{2} & 0 & -b_{2} \\ 0 & H_{3} & 2i\omega_{k}-c_{1} & -c_{2} \\ -d_{1}e^{-2i\omega_{k}\tau_{k}^{(j)}} & H_{4} &-d_{1}e^{-2i\omega_{k}\tau_{k}^{(j)}} & 2i\omega_{k} \end{array}\displaystyle \right ), \\& \Delta_{13}=\det \left ( \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{}} 2i\omega_{k}-a_{1} & 0 & H_{1} & -a_{2} \\ 0 & 2i\omega_{k}-b_{1} & H_{2} & -b_{2} \\ 0 & 0 & H_{3} & -c_{2} \\ -d_{1}e^{-2i\omega_{k}\tau_{k}^{(j)}} & -d_{1}e^{-2i\omega_{k}\tau_{k}^{(j)}} &H_{4} & 2i\omega_{k} \end{array}\displaystyle \right ), \\& \Delta_{14}=\det \left ( \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{}} 2i\omega_{k}-a_{1} & 0 & 0 & H_{1} \\ 0 & 2i\omega_{k}-b_{1} & 0 & H_{2} \\ 0 & 0 & 2i\omega_{k}-c_{1} & H_{3} \\ -d_{1}e^{-2i\omega_{k}\tau_{k}^{(j)}} & -d_{1}e^{-2i\omega_{k}\tau_{k}^{(j)}} &-d_{1}e^{-2i\omega_{k}\tau_{k}^{(j)}} & H_{4} \end{array}\displaystyle \right ). \end{aligned}$$

Similarly, substituting (3.37) and (3.42) into (3.40), we have

$$ \biggl( \int_{-\tau_{k}^{(j)}}^{0} d\eta(\theta) \biggr)E_{2}=(P_{1}, P_{2}, P_{3}, P_{4})^{T}. $$

(3.45)

That is,

$$ \left ( \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{}} a_{1} & 0 & 0 & a_{2} \\ 0 & b_{1} & 0 & b_{2} \\ 0 & 0 & c_{1} & c_{2} \\ d_{1} & d_{1} & d_{1} & 0 \end{array}\displaystyle \right )\left ( \textstyle\begin{array}{@{}c@{}} E_{2}^{(1)} \\ E_{2}^{(2)} \\ E_{2}^{(3)} \\ E_{2}^{(4)} \end{array}\displaystyle \right ) =\left ( \textstyle\begin{array}{@{}c@{}} P_{1} \\ P_{2} \\ P_{3}\\ P_{4} \end{array}\displaystyle \right ). $$

(3.46)

Hence,

$$ E_{2}^{(1)}=\frac{\Delta_{21}}{\Delta_{2}},\qquad E_{2}^{(2)}=\frac{\Delta _{22}}{\Delta_{2}},\qquad E_{2}^{(3)}= \frac{\Delta_{23}}{\Delta_{2}},\qquad E_{2}^{(4)}=\frac{\Delta _{24}}{\Delta_{2}}, $$

(3.47)

where

$$\begin{aligned}& \Delta_{2}=\det \left ( \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{}} a_{1} & 0 & 0 & a_{2} \\ 0 & b_{1} & 0 & b_{2} \\ 0 & 0 & c_{1} & c_{2} \\ d_{1} & d_{1} & d_{1} & 0 \end{array}\displaystyle \right ), \\& \Delta_{21}=\det \left ( \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{}} -P_{1} & 0 & 0 & a_{2} \\ -P_{2} & b_{1} & 0 & b_{2} \\ -P_{3} & 0 & c_{1} & c_{2} \\ -P_{4} & d_{1} & d_{1} & 0 \end{array}\displaystyle \right ), \\& \Delta_{22}=\det \left ( \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{}} a_{1} & -P_{1} & 0 & a_{2} \\ 0 & -P_{2} & 0 & b_{2} \\ 0 & -P_{3} & c_{1} & c_{2} \\ d_{1} & -P_{4} & d_{1} & 0 \end{array}\displaystyle \right ), \\& \Delta_{23}=\det \left ( \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{}} a_{1} & 0 & -P_{1} & a_{2} \\ 0 & b_{1} & -P_{2} & b_{2} \\ 0 & 0 & -P_{3} & c_{2} \\ d_{1} & d_{1} & -P_{4} & 0 \end{array}\displaystyle \right ), \\& \Delta_{24}=\det \left ( \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{}} a_{1} & 0 & 0 & -P_{1} \\ 0 & b_{1} & 0 & -P_{2} \\ 0 & 0 & c_{1} & -P_{3} \\ d_{1} & d_{1} & d_{1} & -P_{4} \end{array}\displaystyle \right ). \end{aligned}$$

From (3.32), (3.34), (3.44), (3.47), we can calculate $g_{21}$ and derive the following values:

$$\begin{aligned}& c_{1}(0)=\frac{i}{2\omega_{k}} \biggl(g_{20}g_{11}-2|g_{11}|^{2}- \frac {|g_{02}|^{2}}{3} \biggr)+\frac{g_{21}}{2}, \\& \mu_{2}=-\frac{\operatorname{Re}\{c_{1}(0)\}}{\operatorname{Re}\{\lambda'(\tau _{k}^{(j)})\} }, \\& \beta_{2}=2\operatorname{Re} {\bigl(c_{1}(0)\bigr)}, \\& T_{2}=-\frac{\operatorname{Im}{\{c_{1}(0)\}}+\mu_{2}\operatorname{Im}\{\lambda'(\tau _{k}^{(j)})\}}{\omega_{k}}. \end{aligned}$$

These formulas give a description of the Hopf bifurcation periodic solutions of (1.4) at $\tau=\tau_{k}^{(j)}$ on the center manifold. From the discussion above, we have the following result.

Theorem 3.3

For system (1.4), if (H1)-(H4) hold, the periodic solution is supercritical (subcritical) if $\mu_{2}>0$ ($\mu_{2}<0$); the bifurcating periodic solutions are orbitally asymptotically stable with asymptotical phase (unstable) if $\beta_{2}<0$ ($\beta_{2}>0$); the periods of the bifurcating periodic solutions increase (decrease) if $T_{2}>0$ ($T_{2}<0$).

4 Numerical examples

In this section, we present some numerical results of system (1.4) to verify the analytical predictions obtained in the previous section. From Section 3, we may determine the direction of a Hopf bifurcation and the stability of the bifurcation periodic solutions. Let us consider the following special case of system (1.4):

$$ \left \{ \textstyle\begin{array}{l} \dot{x}_{1}(t)=0.5x_{1}(t-\tau) [\frac {1-p(t)}{6.25x_{1}(t)}-0.5x_{1}(t)p(t) ], \\ \dot{x}_{2}(t)=0.5x_{2}(t-\tau) [\frac {1-p(t)}{6.25x_{2}(t)}-0.5x_{2}(t)p(t) ], \\ \dot{x}_{3}(t)=0.5x_{3}(t-\tau) [\frac {1-p(t)}{6.25x_{3}(t)}-0.5x_{3}(t)p(t) ], \\ \dot{p}(t)=0.3p(t)[x_{1}(t-\tau)+x_{2}(t-\tau)+x_{3}(t-\tau)-2]. \end{array}\displaystyle \right .$$

(4.1)

By some complicated computation by means of Matlab 7.0, we get $\omega_{0}\approx0.9824$, $\tau_{0}\approx1.85$, $\lambda'(\tau_{0})\approx2.1022-3.1513i$. Thus we can calculate the following values: $c_{1}(0)\approx-2.9542-22.2355i$, $\mu_{2}\approx0.5642$, $\beta_{2}\approx-4.4636$, $T_{2}\approx22.1327$. We see that the conditions indicated in Theorem 2.3 are satisfied. Furthermore, it follows that $\mu_{2}>0$ and $\beta_{2}<0$. Choose $\tau=1.65<\tau_{0}\approx1.85$. Thus, the equilibrium $(x_{1}^{*}, x_{2}^{*}, x_{3}^{*}, p^{*})$ is stable when $\tau<\tau_{0}$, which is illustrated by the computer simulations (see Figure 1 and Figure 2). When τ passes through the critical value $\tau_{0}\approx6.2$, the equilibrium $(x_{1}^{*}, x_{2}^{*}, x_{3}^{*}, p^{*})$ loses its stability and a Hopf bifurcation occurs, i.e., a family of periodic solutions bifurcate from the equilibrium $(x_{1}^{*}, x_{2}^{*}, x_{3}^{*}, p^{*})$. Choose $\tau=1.97>\tau_{0}\approx1.85$. Since $\mu_{2}>0$ and $\beta_{2}<0$, the direction of the Hopf bifurcation is $\tau>\tau_{0}$, and these bifurcating periodic solutions from $(x_{1}^{*}, x_{2}^{*}, x_{3}^{*}, p^{*})$ at $\tau_{0}$ are stable; they are depicted in Figure 3 and Figure 4.

Figure 1

Dynamic behavior of system ( 4.1 ): times series of $\pmb{x_{i}}$ ( $\pmb{i=1,2,3}$ ) and $\pmb{p(t)}$ . A Matlab simulation of the asymptotically stable origin to system (4.1) with $\tau=1.65<\tau_{0}\approx1.85$. The initial value is $(0.5, 0.5, 0.5, 0.5)$.

Figure 2

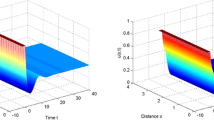
Dynamic behavior of system ( 4.1 ): projection on $\pmb{x_{1}}$ - p , $\pmb{x_{2}}$ - p , $\pmb{x_{3}}$ - p plane and projection on $\pmb{x_{2}}$ - $\pmb{x_{3}}$ - p space. A Matlab simulation of the asymptotically stable origin to system (4.1) with $\tau=1.65<\tau_{0}\approx1.85$. The initial value is $(0.5, 0.5, 0.5, 0.5)$.

Figure 3

Dynamic behavior of system ( 4.1 ): times series of $\pmb{x_{i}}$ ( $\pmb{i=1,2,3}$ ) and p . A Matlab simulation of a periodic solution to system (4.1) with $\tau=1.97>\tau_{0}\approx1.85$. The initial value is $(0.5, 0.5, 0.5, 0.5)$.

Figure 4

Dynamic behavior of system ( 4.1 ): projection on the $\pmb{x_{1}}$ - p , $\pmb{x_{2}}$ - p , $\pmb{x_{3}}$ - p plane and projection on the $\pmb{x_{2}}$ - $\pmb{x_{3}}$ - p space, respectively. A Matlab simulation of a periodic solution to system (4.1) with $\tau=1.97>\tau_{0}\approx1.85$. The initial value is $(0.5, 0.5, 0.5, 0.5)$.

5 Conclusions

In this paper, we have investigated the properties of Hopf bifurcation in an exponential RED algorithm with communication delay. It is shown that under certain conditions, the Hopf bifurcation occurs as the delay τ passes through some critical values $\tau=\tau_{k}^{(j)}$, $k, j=0,1,2,\ldots$ . Moreover, the direction of the Hopf bifurcation and the stability of the bifurcating periodic orbits are derived by applying the normal form theory and the center manifold theorem.