Introduction

This paper is an enhanced and updated version of conference paper [1]. Forecasting is a critical requirement for planning, in all facets of human life. Forecasts of all kinds hinge on available data. Whereas some data are amenable to forecasting, others have high levels of uncertainty which present challenges to forecast models. In recent times, the grey system model GM(1,1) has gained popularity as a forecasting model capable of dealing with uncertainties associated with available data for forecasting [2]. It is noted to be computational efficient and can deal with systems that have limited data samples and poor information [2,3,4].

Statistical models for forecasting need a high number of data samples, and several assumptions [5]. However, the data for many systems do not obey statistical rules [6]. Computational intelligent models also require a high volume of training data that are largely not available [7]. On the other hand, the GM(1,1) overcomes the inherent deficiencies of statistical and computational intelligent methods and accurately makes forecasts using limited, incomplete and uncertain data.

However, GM(1, 1) has shortcomings that adversely impact on its performance [8]. It therefore requires additional algorithms to enhance its performance [9,10,11,12,13]. Researchers have therefore pursued the development of new algorithms to enhance its performance.

The identified areas of optimization in GM(1,1) are [7,8,9,10,11,12,13,14]: (1) the neglect of the first entry in the prediction, which reduces the data utilization efficiency, (2) deficiencies in arriving at optimal background values and (3) determining the initial condition in the model’s time response function.

The work in [10] stresses the fact that the background value (BV) is the principal element that determines the accuracy of the model. The BV is produced using adjacent neighbor weight (ANW) or coefficient that is normally set to 0.5. This suggests that adjacent two-time series data have equal impact on the model. However, a data sample may be biased towards the left or right. Hence, to improve forecast accuracy, it is necessary to accurately generate the BV using weights that consider the nature of data samples. This need is yet to be addressed in literature.

To contribute to address this need, this work uses the PSO to find optimal ANWs to produce optimal BVs. The optimal ANWs will not be fixed, but dependent on the nature of the data samples. The proposed method will understand the progression of data samples to produce optimal ANWs to enhance forecast accuracy. The proposed PSO-GM(1,1) outperforms GM(1,1) and other methods in literature.

The paper is sectioned as follows: “Methods” section describes the methods used. In “Traditional grey system model” section, GM(1,1) is explained. The PSO is explained in “Particle swarm optimization” section. “Proposed PSO-GM(1,1)” section outlines the proposed PSO-GM(1,1). The approach for testing is outlined in “Approach for testing” section. “Results and discussion” section analysis and discusses the test results. Conclusions drawn are summarized in “Conclusion” section.

Methods

The study sought to enhance the forecast accuracy of GM(1,1). To achieve this, GM(1,1) was studied to understand its operation and identify aspects that can be enhanced to maximize its forecast performance. Having identified aspects of the model that can be enhanced, an appropriate tool for realizing the enhancements was found. The tool was then studied to gain full understanding of its operations. Following this, the needed enhancements to the GM(1,1) were made. Data sets were then generated to test the effectiveness of the enhancements made and to compare the enhanced model’s performance with the traditional model and other models in literature that offer some improvements to the GM(1,1). The data sets were monotonic increasing and monotonic decreasing data sets generated using appropriate mathematical equations. Additionally, data were produced by monitoring the energy consumption of a laptop computer, desktop computer, printer, and photocopier. The energy consumptions of the plug loads were monitored using a smart plug (Energenie MIHO005 Adaptor Plus).

Traditional grey system model

Given a non-negative sequence of raw data \(X^{(0)} \left( k \right)\), given as [15, 16]:

$$X^{(0)} \left( k \right) = \left( {X^{(0)} (1),X^{(0)} (2),\;.\;.\;.\;X^{(0)} (n)} \right)$$
(1)

the accumulated generated sequence, \(X^{(1)} \left( k \right)\) is given as

$$X^{(1)} \left( k \right) = \left( {X^{(1)} (1),X^{(1)} (2),\;.\;.\;.\;X^{(1)} (n)} \right)$$
(2)

where

$$X^{(1)} \left( k \right) = \sum\limits_{k = 1}^{n} {X^{(0)} (k)} ,\,k = 1,2,3,...,n$$

Thus, \(X^{(1)} \left( 1 \right) = X^{(0)} \left( 1 \right).\)

The calculated background value, \(Z^{(1)} \left( k \right)\), is given as

$$Z^{(1)} \left( k \right) = \left[ {0.5X^{(1)} \left( k \right) + 0.5X^{(1)} \left( {k - 1} \right)} \right]\,k = 1,2,3,...,n$$
(3)

The basic form of the first order model GM (1,1) is given by the following:

$$X^{(1)} \left( k \right) + aZ^{(1)} \left( k \right) = m$$
(4)

where a is the development coefficient and m is the grey action quantity.

From (4), the whitenization equation of the model GM (1,1) is given as

$$\frac{{dX^{(1)} }}{dt} + aX^{(1)} = m$$
(5)

The coefficients a and m can be obtained as follows:

$$\left[ {a,m} \right]^{T} = \left( {B^{T} B} \right)^{ - 1} B^{T} Y$$
(6)

where

$$Y = \left[ {\begin{array}{*{20}c} {X^{(0)} (1)} \\ {X^{(0)} (2)} \\ . \\ . \\ . \\ {X^{(0)} (n)} \\ \end{array} } \right]\,{\text{and}}\,B = \left[ {\begin{array}{*{20}c} { - Z^{(1)} (2)} & 1 \\ { - Z^{(1)} (3)} & 1 \\ . & . \\ . & . \\ . & . \\ { - Z^{(1)} (n)} & 1 \\ \end{array} } \right].$$

If the time response solution of the whitenization equation is given by the following:

$$\hat{X}^{(1)} \left( t \right) = \left( {X^{(1)} (1) - \tfrac{m}{a}} \right)e^{ - at} + \tfrac{m}{a},$$
(7)

then, the time response of the sequence of GM (1,1) can be obtained using (8)

$$\hat{X}^{(1)} \left( {k + 1} \right) = \left( {X^{(0)} (1) - \tfrac{m}{a}} \right)e^{ - ak} + \tfrac{m}{a}$$
(8)

Therefore, the predicted values can be found using

$$\hat{X}^{(0)} \left( {k + 1} \right) = \hat{X}^{(1)} \left( {k + 1} \right) - \hat{X}^{(1)} \left( k \right).$$
(9)

Thus,

$$\hat{X}^{(0)} \left( {k + 1} \right) = \left( {1 - e^{a} } \right)\left( {X^{(0)} (1) - \tfrac{m}{a}} \right)e^{ - ak} .$$
(10)

Particle swarm optimization

PSO is a widely used optimization algorithm in engineering [17]. It mimics the social behavior of animals. In PSO, every individual solution is viewed as a particle. Each solution (particle) is given a solution number, say (i). A swarm is created when solutions are combined. The technique initializes the position of each solution, in addition to other constants. This is defined by a coordinate in n-dimensional space into the problem (objective or fitness function) to be optimized. Each solution remembers its own previous best position (Pbest) and the best position of the entire swarm (Gbest). Each solution then alters its position by updating its velocity until the optimal solution is found [17].

Proposed PSO-GM(1,1)

The performance of GM(1,1) has been enhanced by using PSO, to find an optimal value for adjacent neighbor weight (ANW) that will optimally construct the background value, \(Z^{(1)} (k)\). Let (11) be the modification of (3), in line with the proposed method, to obtain the ANW.

$$Z^{(1)} (k) = \left[ {pX^{(1)} (k) + pX^{(1)} (k - 1)} \right]\,k = 1,2,3,...,n$$
(11)

In (11), p is the ANW. The parameters \(B^{T} B\) and \(B^{T} Y\) needed to find the development coefficient, a, and the grey action quantity, m, in (6) can be further determined as follows:

$$B^{T} B = \left[ {\begin{array}{*{20}c} { - Z^{(1)} (2)} & { - Z^{(1)} (3)} & . & . & . & { - Z^{(1)} (n)} \\ 1 & 1 & . & . & . & 1 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} { - Z^{(1)} (2)} & 1 \\ { - Z^{(1)} (3)} & 1 \\ . & . \\ . & . \\ . & . \\ { - Z^{(1)} (n)} & 1 \\ \end{array} } \right],$$
(12)
$$B^{T} Y = \left[ {\begin{array}{*{20}c} { - Z^{(1)} (2)} & { - Z^{(1)} (3)} & . & . & . & { - Z^{(1)} (n)} \\ 1 & 1 & . & . & . & 1 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {X^{(0)} (2)} \\ {X^{(0)} (3)} \\ . \\ . \\ . \\ {X^{(0)} (n)} \\ \end{array} } \right]$$
(13)

Therefore,

$$\left[ {a,m} \right]^{T} = \left( {B^{T} B} \right)^{ - 1} B^{T} Y = \left[ {\begin{array}{*{20}c} {\frac{{\sum\limits_{k = 2}^{n} {Z^{(1)} (k)\sum\limits_{k = 2}^{n} {X^{(0)} (k) - (n - 1)\sum\limits_{k = 2}^{n} {Z^{(1)} (k)X^{(0)} (k)} } } }}{{(n - 1)\sum\limits_{k = 2}^{n} {\left( { - Z^{(1)} (k)} \right)^{2} - \left( {\sum\limits_{k = 2}^{n} {Z^{(1)} (k)} } \right)^{2} } }}} \\ {\frac{{\sum\limits_{k = 2}^{n} {Z^{(1)} (k)}^{2} \sum\limits_{k = 2}^{n} {X^{(0)} (k) - \sum\limits_{k = 2}^{n} {Z^{(1)} (k)} X^{(0)} (k)\sum\limits_{k = 2}^{n} {Z^{(1)} (k)} } }}{{(n - 1)\sum\limits_{k = 2}^{n} {\left( {Z^{(1)} (k)} \right)}^{2} - \left[ {\sum\limits_{k = 2}^{n} {Z^{(1)} (k)} } \right]^{2} }}} \\ \end{array} } \right].$$
(14)

Hence, substituting for a and m in (10)

$$\begin{aligned} \hat{X}^{(0)} \left( {k + 1} \right) & = \left( {1 - e^{{\frac{{\sum\limits_{k = 2}^{n} {Z^{(1)} (k)\sum\limits_{k = 2}^{n} {X^{(0)} (k) - (n - 1)\sum\limits_{k = 2}^{n} {Z^{(1)} (k)X^{(0)} (k)} } } }}{{(n - 1)\sum\limits_{k = 2}^{n} {\left( { - Z^{(1)} (k)} \right)^{2} - \left( {\sum\limits_{k = 2}^{n} {Z^{(1)} (k)} } \right)^{2} } }}}} } \right) \\ & \quad \times \left( {X^{(0)} (1) - \tfrac{{\frac{{\sum\limits_{k = 2}^{n} {Z^{(1)} (k)}^{2} \sum\limits_{k = 2}^{n} {X^{(0)} (k) - \sum\limits_{k = 2}^{n} {Z^{(1)} (k)} X^{(0)} (k)\sum\limits_{k = 2}^{n} {Z^{(1)} (k)} } }}{{(n - 1)\sum\limits_{k = 2}^{n} {\left( {Z^{(1)} (k)} \right)}^{2} - \left[ {\sum\limits_{k = 2}^{n} {Z^{(1)} (k)} } \right]^{2} }}}}{{\frac{{\sum\limits_{k = 2}^{n} {Z^{(1)} (k)\sum\limits_{k = 2}^{n} {X^{(0)} (k) - (n - 1)\sum\limits_{k = 2}^{n} {Z^{(1)} (k)X^{(0)} (k)} } } }}{{(n - 1)\sum\limits_{k = 2}^{n} {\left( { - Z^{(1)} (k)} \right)^{2} - \left( {\sum\limits_{k = 2}^{n} {Z^{(1)} (k)} } \right)^{2} } }}}}} \right) \\ & \times e^{{ - \left( {\frac{{\sum\limits_{k = 2}^{n} {Z^{(1)} (k)\sum\limits_{k = 2}^{n} {X^{(0)} (k) - (n - 1)\sum\limits_{k = 2}^{n} {Z^{(1)} (k)X^{(0)} (k)} } } }}{{(n - 1)\sum\limits_{k = 2}^{n} {\left( { - Z^{(1)} (k)} \right)^{2} - \left( {\sum\limits_{k = 2}^{n} {Z^{(1)} (k)} } \right)^{2} } }}} \right)k}} \\ \end{aligned}$$
(15)

Thus, to accurately determine \(\hat{X}^{(0)} \left( {k + 1} \right)\), accurate values of \(Z^{(1)} (k)\) must be found. Moreover, the accuracy of \(Z^{(1)} (k)\), depends on the optimality of the value of p. This work therefore focuses on optimally determining the value of p to produce accurate values of \(\hat{X}^{(0)} \left( {k + 1} \right)\). The optimal value for p, is determined using the PSO. This is achieved by minimizing the sum of squared errors associated with the forecast.

For data \(X^{(0)} (k)\), forecasted as \(\hat{X}^{(0)} (k + 1)\), the forecast error, \(E_{k}\), is given by the following:

$$E_{k} = X^{(0)} (k) - \hat{X}^{(0)} (k + 1),\,k = 1,2,3,...,n$$
(16)

The sum of squared errors, E, is given as

$$E = \sum\limits_{k = 1}^{n} {\left( {X^{(0)} (k) - \hat{X}^{(0)} (k + 1)} \right)^{2} } ,\,k = 1,2,3,...,n$$
(17)

Let the fitness function, f, of the PSO be the sum of squared error of GM(1,1). Thus,

$$f = \sum\limits_{k = 1}^{n} {\left( {X^{(0)} (k) - \hat{X}^{(0)} (k + 1)} \right)^{2} } ,\,k = 1,2,3,...,n$$
(18)

Thus, PSO’s task is to find the optimal value of p that makes the sum of squared errors equal to zero. In applying PSO, for this work, particle (i) refers to the possible values for p, in (11). The values for p range from 0 to 1. The position (\(X_{i(p)} \left( t \right)\)) refers to the solution value that p takes and the velocity (\(V_{i(p)} \left( t \right)\)) refers to the rate at which the current value of p moves towards the optimal value. Each value or position runs through the objective function in (18) to find the fitness values. After each iteration, the best position or value so far (\(P_{ibest(p)}\)) is chosen for each particle. Also, the best position for all the particles (\(G_{best(p)}\)) is chosen. These values together with two random values r1 and r2, and two learning constants c1 and c2 are used to update the velocity \(V_{i(p)} \left( {t + 1} \right)\)) as shown in (19) and then the new position, using (20). These steps are continued until a stopping criterion, which could be the total number of iterations, is met.

$$V_{i(p)} \left( {t + 1} \right) = wV_{i(p)} \left( t \right) + r_{1} c_{1} \left( {P_{ibest(p)} - X_{i(p)} (t)} \right) + r_{2} c_{2} \left( {G_{best(p)} - X_{i(p)} (t)} \right)$$
(19)
$$X_{i(p)} \left( {t + 1} \right) = X_{i(p)} \left( t \right) + V_{i(p)} \left( {t + 1} \right)$$
(20)

  • w is the inertia weight factor,

  • \(V_{i(p)} \left( t \right)\) is the initial (or previous) velocity vector,

  • \(P_{ibest(p)}\) is the personal best position of particle i,

  • \(G_{best(p)}\) is the global best in the entire swarm,

  • \(X_{i(p)} \left( t \right)\) is the current position of particle i and

  • \(X_{i(p)} \left( {t + 1} \right)\) is the updated position of particle i.

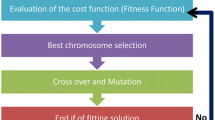
Figure 1 shows the flowchart for the proposed PSO-improved grey model. The operation of the improved model is outlined as follows:

  1. 1.

    Initialize PSO parameters (w, r1, r2, c1, and c2) and assume a set of values for p. At this stage, each assumed value of p is considered as a personal best solution, pending the determination of the global best solution, after an iteration.

  2. 2.

    Evaluate objective function in (18).

  3. 3.

    Update each solution’s personal best (\(P_{ibest(p)}\)).

  4. 4.

    Update the global best (\(G_{best(p)}\)).

  5. 5.

    Update each solution’s velocity (\(V_{i(p)} \left( {t + 1} \right)\)) using (19).

  6. 6.

    Update each solution’s position (\(X_{i(p)} \left( t \right)\)) using (20).

  7. 7.

    Choose the best solution of p, as the optimal ANW,\(p_{optimal}\), when the maximum iteration is attained.

  8. 8.

    Update the background value in (11) using the optimal adjacent neighbor weight (\(p_{optimal}\)).

  9. 9.

    Perform forecast and display results.

Fig. 1
figure 1

Flowchart of PSO-GM(1,1)

Full size image

Approach for testing

The performance of the PSO-GM(1,1) was assessed using six data sets. Two of the six data sets were randomly generated monotonic increasing and decreasing data. The monotonic increasing data set was generated using (21) while the monotonic decreasing data set was produced using (22). This approach to data generation was borrowed from [18, 19]. The generated monotonic data sets were used to compare the forecast accuracy of the developed PSO-GM(1,1) and GM(1,1).

$$X\left( t \right) = 2e^{t} ,\;\;\;\;\;t = 1,2,...,n$$
(21)
$$X\left( t \right) = 8e^{ - t} ,\;\;\;\;\;t = 1,2,...,n$$
(22)

The third, fourth, fifth and sixth data sets were measured weekly energy consumptions of a laptop computer, desktop computer, printer, and photocopier. The energy consumptions were measured using Energenie MIHO005 Adaptors [20]. These data sets were used to further evaluate the forecast accuracy of the technique and to compare it with GM(1,1) and two other models presented in [18, 19]. The method in [18] modifies the background value of GM(1,1) while that in [19] modifies the initial condition of GM(1,1).

The mean absolute percentage error (MAPE) index was employed to assess the overall performances of the models. The lower the MAPE, the higher the accuracy of the model, and vice versa. With the percentage forecast error,\(E_{k}\), given by (23), the MAPE is determined using (24).

$$E_{k} = \frac{{X^{(0)} (k) - \hat{X}^{(0)} (k + 1)}}{{X^{(0)} (k)}} \times 100$$
(23)
$$MAPE = \frac{1}{N}\sum\limits_{{}}^{{}} {\left[ {\frac{{X^{(0)} (k) - \hat{X}^{(0)} (k + 1)}}{{X^{(0)} (k)}}} \right]} \times 100$$
(24)

\(X^{(0)} (k)\) is the original value and \(\hat{X}^{(0)} (k + 1)\) is the forecasted value.

Results and discussion

Figure 2 presents the prediction results for a monotonic increasing data, using GM(1,1) and that using the proposed improved grey model (i.e., PSO-GM(1,1)). The figure shows the actual monotonic increasing data and the corresponding values predicted by the PSO-GM(1,1) and the GM(1,1). For this data set, the optimal adjacent neighbor weight was determined, using the PSO-GM(1,1), to be 0.418, instead of the constant value of 0.5 used by GM(1,1). It is noted from Fig. 2 that the values outputted by PSO-GM(1,1) near perfectly matches the actual data (the plot for PSO-GM(1,1) has even covered that for the actual data) while those produced by GM(1,1) have significant deviations. For example, for data point 5 which has a value of 296.826, the output of the PSO-GM(1,1) is 296.857 whereas that of the GM(1,1) is 209.179. For this data value, the percentage error in prediction for the PSO-GM(1,1) computed using (23), is 0.01%, whereas the percentage error associated with the GM(1,1) is 29.53%. Table 1 presents the percentage errors for all the predictions. It is noted from Table 1 that the errors associated with PSO-GM(1,1) are minimal and much lower than those associated with the GM(1,1). For the entire monotonic increasing data, the MAPE for the proposed model was obtained to be 0.007% while that for the GM(1,1) was 20.38%. Thus, the PSO-GM(1,1) has a better accuracy than the GM(1,1).

Fig. 2
figure 2

Performance comparison of PSO-GM(1,1) and GM(1,1) for a monotonic increasing data

Full size image
Table 1 Percentage prediction errors for PSO-GM(1,1) and GM(1,1) for a monotonic increasing data
Full size table

Figure 3 also shows the forecast results for a monotonic decreasing data, using the PSO-GM(1,1) and GM(1,1). The optimal ANW was determined to be 0.5808 by the PSO-GM(1,1). For this data set too, the forecasted values by the PSO-GM(1,1) closely mirror the actual data while those produced by the GM(1,1) have substantial deviations. For example, for data point 5 with a data value of 0.054, the value predicted by the PSO-GM(1,1) is 0.054 whereas that of the GM(1,1) is 0.065. For this data value, the percentage error in prediction for the PSO-GM(1,1) computed using (23) is 0% whereas the percentage error associated with the GM(1,1) is -20.37%. Table 2 shows the errors associated with the various predictions. It is noted from Table 2 that the PSO-GM(1,1) has lower errors. The MAPE for the improved model is 0.057% while that for the GM(1,1) is 13.407%. Therefore, the forecast accuracy of the PSO-GM(1,1) is noted to be much higher than that of the GM(1,1). The superior results of the PSO-GM(1,1) show that keeping the ANW constant at 0.5 (as is the case of GM(1,1)) results in significant errors in forecasts while using the proposed approach to find optimal values of ANW yields high accuracies in forecasts.

Fig. 3
figure 3

Performance comparison of PSO-GM(1,1) and GM(1,1) for a monotonic decreasing data

Full size image
Table 2 Percentage prediction errors for PSO-GM(1,1) and GM(1,1) for a monotonic decreasing data
Full size table

Figure 4 shows the forecast results for the energy consumption data for a laptop, using the proposed PSO-GM(1,1), the GM(1,1) and two other models in literature. The two other models are models presented in [18, 19]. The model in [18] attempts to improve the forecast accuracy of the GM(1,1) by modifying the background value while that in [19] offers improvements through the modification of the initial condition. For this forecast, the optimal ANW was determined using the PSO-GM(1,1) to be 0.537. It is noted from Fig. 4 that the PSO-GM(1,1) outperforms all the other models in accurately forecasting the energy consumption for weeks 1, 2 and 3. The values determined by the PSO-GM(1,1) are the closest to the actuals. For example, for the energy consumption data of 450.031 for week 1, the PSO-GM(1,1) gave a value of 450.570 (with a minimal deviation of -0.539 while the GM(1,1) and the models in [18, 19] outputted, 438.564, 473.978 and 429.120, respectively with higher deviations of 11.467, -23.947 and 20.911, respectively. However, for the forecast for week 4, the model in [19] performed better than the PSO-GM(1,1) and all the others. The accuracy of the model in [19] was 100%. The percentage errors in forecasts for the various models are presented in Table 3. The Table shows the PSO-GM(1,1) as having the least percentage deviations from the actual values of the forecasts for weeks 1, 2 and 3 while the method in [19] has the least forecast error for week 4. Overall, the MAPEs are 0.6754% for the PSO-GM(1,1), 1.9560% for GM(1,1), 4.0516% for the model in [18] and 2.9907% for the model in [19]. Thus, the proposed PSO-GM(1,1) has the least overall MAPE and thus outperforms all the other models.

Fig. 4
figure 4

Forecast results for energy data for a laptop, using the various models

Full size image
Table 3 Percentage forecast errors associated with the various models, for energy data for a laptop
Full size table

Figure 5 shows the forecast results for the weekly energy consumption data for a desktop computer, using the PSO-GM(1,1), GM(1,1) and the two other models. For this forecast, the optimal ANW was determined to be 0.462. For this forecast, the results have been presented to four decimal places in order to bring out the marginal difference in values forecasted by the PSO-GM(1,1) and the method in [18]. For this data set, the PSO-GM(1,1) outperformed the GM(1,1) in the forecasts for all weeks. It also outperformed the model in [19] in forecasting data for weeks 1, 2 and 3. The model in [19] however performed better than the PSO-GM(1,1) in forecasting the data for week 4. The performance of the PSO-GM(1,1) was at par with the model in [18]. For weeks 1 and 2, the PSO-GM(1,1) performed marginally better than the model in [18]. Between the two models, the PSO-GM(1,1) was only better than the model in [18] by margins of -0.0003 for week 1 and 0.0010 for week 2. On the other hand, for weeks 3 and 4, the model in [18] was marginally better than the PSO-GM(1,1). The margins for these weeks are 0.0008 and -0.0003 for weeks 3 and 4, respectively. The percentage errors in forecast, for the various models, are presented in Table 4. From Table 4, the PSO-GM(1,1) and the model in [18] have the least and near equal errors. The MAPEs were computed to be 0.0018% for the PSO-GM(1,1), 2.1272% for the GM(1,1), 0.0018% for the model in [18] and 1.1626% for the model in [19]. Thus, overall, the PSO-GM(1,1)’s performance equaled that of the model in [18], but was better than the GM(1,1) and the model in [19].

Fig. 5
figure 5

Forecast results using the various models, for energy data for a desktop computer

Full size image
Table 4 Percentage errors associated with forecasts by the various models, for energy data for a desktop computer
Full size table

Figure 6 shows the forecast results for the energy data for a printer. For this data, the optimal ANW was determined to be 0.1120. The percentage errors in forecast for the various models are presented in Table 5. The PSO-GM(1,1) performed better than GM(1,1) and the method in [18] for week 1 forecast, better than the method in [19] for week 2 forecast, better than GM(1,1) and the method in [18] for week 3, and lastly, better than the methods in [18, 19] for week 4. It had the least MAPE of 8.4135%. The MAPEs for the others are as follows: 9.0802% for GM(1,1), 20.9572% for the method in [18] and 9.0802% for the that in [19]. Consequently, the PSO-GM(1,1) is considered to have performed better than all the others.

Fig. 6
figure 6

Forecast results for energy data for a printer, using the various models

Full size image
Table 5 Percentage forecast errors for energy data for a printer, associated with the various models
Full size table

Figure 7 shows the forecast results for the energy consumption data for a photocopier. For this forecast, the optimal ANW was determined to be 0.4899. It is noted from Fig. 7 that the PSO-GM(1,1) outperforms the model in [18] in the forecasts for all weeks. In comparison with the method in [19], the PSO-GM(1,1) shows better performance for forecasts for weeks 1 and 3. For weeks 2 and 4, the method in [19] outperforms the PSO-GM(1,1). In comparison with the GM(1,1), the PSO-GM(1,1) was only better in relation to the forecast for week 1. The percentage errors in forecast for the various models are presented in Table 6. The MAPEs were computed to be 0.9009% for the PSO-GM(1,1), 0.9012% for GM(1,1), 3.7989% for the model in [18] and 0.9433% for the model in [19]. Thus, the PSO-GM(1,1) outperformed the GM(1,1) and other models in [18, 19]. The near equal performance of the PSO-GM(1,1) and the GM(1,1) is justifiably so because the optimal ANW determined to be 0.4899 by the PSO-GM(1,1) is almost equal the to the fixed ANW value of 0.5 used by the GM(1,1).

Fig. 7
figure 7

Forecast results for energy data for a photocopier, using the various models

Full size image
Table 6 Percentage forecast errors associated with the various models for energy data for a photocopier
Full size table

Conclusion

The forecast accuracy of GM(1,1) has been improved. The improvement lies is in the determination of an optimal value for the adjacent neighbor weight. This improvement has been realized using PSO. The optimal value so determined is not fixed but is dependent on the data used. The improved model has low forecasting error for individual data. The MAPE is also low. The proposed method is found to perform best when data used either continuously decreases or increases. For example, the lowest MAPE for the model, which is 0.007% was recorded for a monotonic increasing data while the model’s worst MAPE of 8.414% was recorded for data that exhibited both increasing and decreasing pattern. The proposed model outperforms GM(1,1) and two other models in literature that sought to improve the forecast accuracy of the GM(1,1). The proposed model is simple to apply and has high accuracy. Future work will consider optimizing the initial condition in the model’s time response function together with the adjacent neighbor weight, to further improve forecast accuracy.